Авторегрессионные модели

Еще одним подходом к описанию основной тенденции временного ряда и прогнозированию является авторегрессионная модель. Ее построению предшествует оценка наличия автокорреляции в изучаемом ряду.

Автокорреляция – это зависимость между последовательными значениями (уровнями) временного ряда. Автокорреляция первого порядка (first-order autocorrelation) оценивает степень зависимости между соседними значениями временного ряда. Автокорреляция второго порядка (second-order autocorrelation) оценивает тесноту связи между значениями, разделенными двумя временными интервалами, и т.д. Интервал времени, разделяющий зависимые уровни динамического ряда, называется лагом (lag). Автокорреляционная зависимость может быть представлена как зависимость между уровнями исходного ряда:

у1, у2, у3, … , уn

и того же ряда, но смещенного на i периодов (моментов) времени:

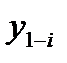, у2-i, у3-i, … , уn-i.

Интервал смещения i – временной лаг (i = 1, i = 2, i = 3 и т. д.).

Наличие автокорреляции проверяется на основе коэффициентов автокорреляции. При этом в качестве результативного признака принимается переменная, содержащая фактические значения уровней исходного ряда динамики, а в качестве факторного признака переменная, содержащая фактические уровни смещенного ряда. Величина временного лага определяет порядок коэффициента автокорреляции.

Для оценки наличия автокорреляции в динамическом ряду необходимо сделать активным рабочий лист с исходным динамическим рядом (переменная «ВГ2001-2010») и запустить процедуру, рассмотренную при анализе автокорреляции в остатках (см. рис. 3.30-3.33). Разница будет заключаться в том, что в данном случае коэффициенты автокорреляции будут рассчитаны для уровней самого ряда. В итоге получаем таблицу (рис. 5.1) и график (рис. 5.2).

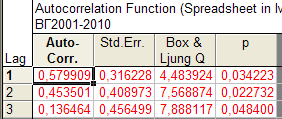
Рис. 5.1. Таблица со значениями коэффициентов автокорреляции для динамического ряда

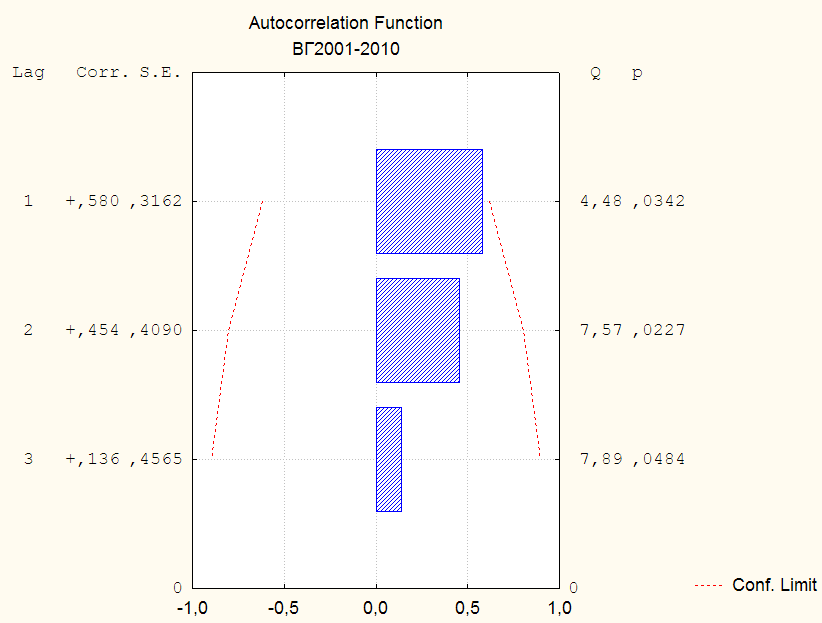
Рис. 5.2. Графическое изображение автокорреляции динамического ряда

Анализируя полученные данные, можно сказать о том, что, несмотря на статистическую значимость коэффициентов автокорреляции на всех трех лагах, ни один из них не превышает теоретического значения. Однако в учебных целях будем считать, что коэффициент автокорреляции на первом лаге, 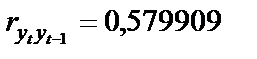, значим и говорит об автокорреляционной зависимости первого порядка.

После подтверждения наличия автокорреляции в динамическом ряду, может идти речь о построении авторегрессионной модели.

Авторегрессионная модель первого порядка (lag=1):

.

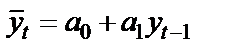Авторегрессионная модель второго порядка:

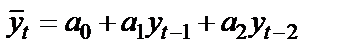и т.д.

Поскольку в нашем примере максимальное значение имеет коэффициент автокорреляции первого порядка, построим авторегрессионную модель, сместив исходный ряд на 1 лаг, т.е. модель первого порядка.

Для вычисления параметров уравнения авторегрессии потребуется создать дополнительную переменную 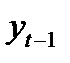. Воспользуемся тем же приемом, что и при расчете показателей изменения уровней динамического ряда. Выберем меню Statistics/Advanced Linear/Nonlinear Models/Times Series/Forecasting, в качестве переменной используем исходные данные («ВГ2001-2010). Нажимаем кнопку OK (transformations, autocorrelations, crosscorrelations, переходим на закладку Shift и в поле Shift (Lag) Series Forward ставим 1. Далее нажимаем ОК (Transform selected series) и сохраняем полученные данные с помощью кнопки Save variables. Добавляем данные в нашу рабочую книгу с помощью кнопки Add to Workbook. В результате получаем таблицу с двумя переменными, первая – исходный ряд, а вторая – ряд, смещенный на 1 период. Длина переменных должна быть одинаковой, для чего нужно удалить первую и последнюю строки, содержащие пустые элементы (рис. 5.3).

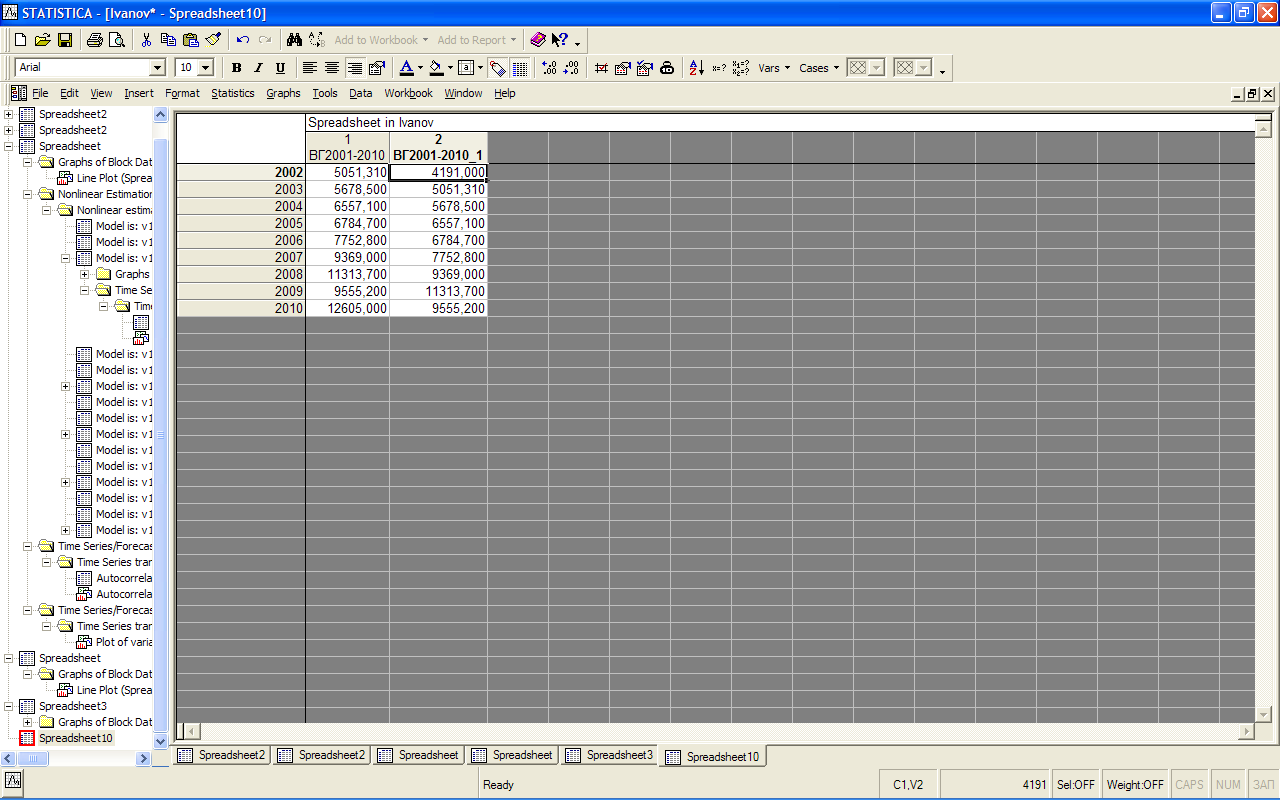
Рис. 5.3. Исходный и смещенный динамические ряды с удаленными данными для построения авторегрессионной модели

Процедура расчета численных значений коэффициентов уравнения авторегрессии идентична определению параметров уравнений для различных трендовых моделей и осуществляется с помощью меню Statistics/Advanced Linear/Nonlinear Models/Nonlinear Estimation. При этом в качестве зависимой переменной выбирается исходный ряд, в качестве независимой – ряд, сдвинутый на лаг назад, так как нас интересует зависимость текущего уровня от предыдущего. Результаты на рис. 5.4., 5.5.

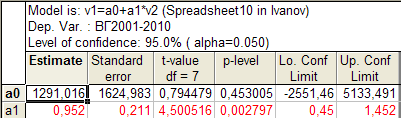
Рис. 5.4. Результаты расчета параметров авторегрессионной модели

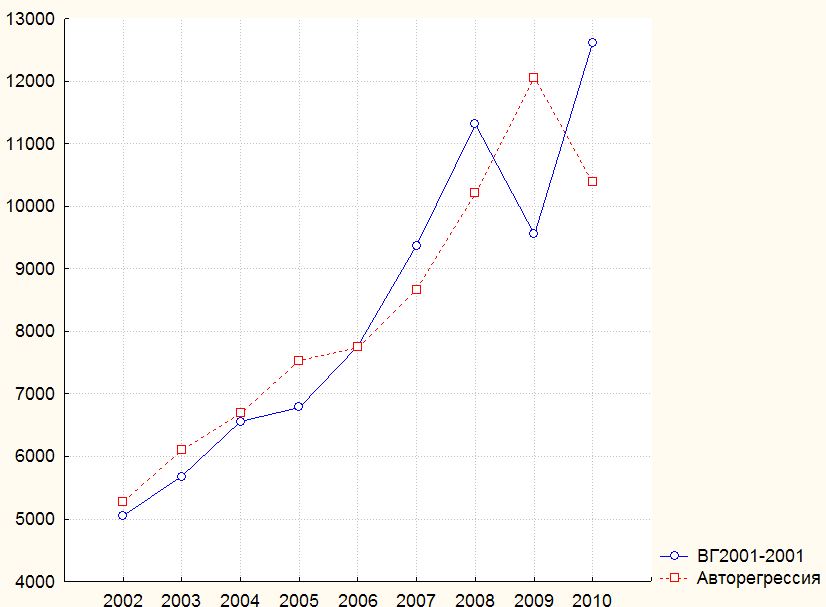
Рис. 5.5. Графическое представление динамического ряда

и авторегрессионной функции

Соответственно, уравнение авторегрессии имеет вид:

.

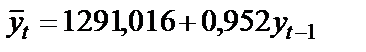Как правило, авторегрессионная модель позволяет лучше, чем трендовая, описать предысторию процесса и получить более точный прогноз. Но для этого необходимо, чтобы уравнение и все его параметры были статистически значимы.

Поскольку в нашем примере один из параметров уравнения авторегрессии статистически незначим, оно не может быть использовано для прогнозирования.

При наличия возможности прогнозирования по авторегрессионной модели все действии, включая расчет прогноза, доверительных интервалов и построение графического изображения осуществляются аналогично экстраполяции трендовых моделей, но не стоит забывать о сокращение числа уровней ряда