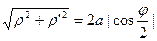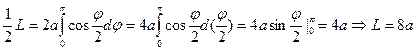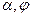Длина дуги в полярных координатах

Лекция 10. Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. Несобственные интегралы.

Определение 1

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена ее стремится к нулю.

Определение 2

Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке.

Кривая задана уравнением 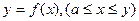(1) f’(x) – непрерывна на отрезке [a,b].

Теорема Всякая гладкая кривая (1) имеет определенную конечную длину дуги.

Доказательство

Впишем в данную гладкую кривую (1) ломаную линию

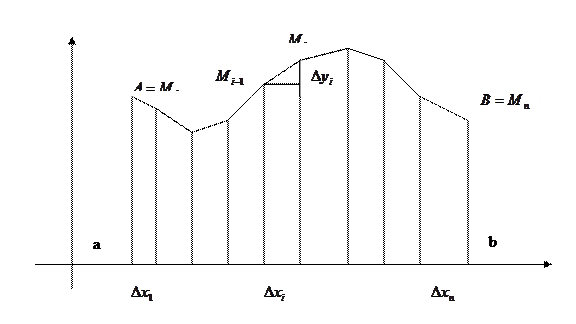
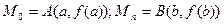Проектируя звенья 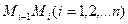ломаной на ось ОХ, получим разбиение отрезка [a,b] на систему отрезков 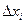. Пусть 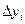- приращение функции y=f(x) на отрезке [a,b]. По теореме Пифагора имеем 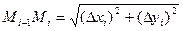. Применяя теорему Лагранжа о конечном приращении функции, получим

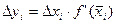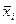, где - некоторая промежуточная точка отрезка 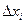. Отсюда

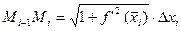. Длина всей ломаной линии 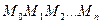(то есть ее периметр) равна 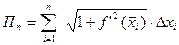Для нахождения длины L кривой (1) в последнем выражении переходим к пределу пр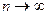и и 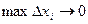. Таким образом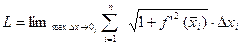

Получаем предел интегральной суммы для непрерывной функции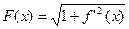

Поэтому 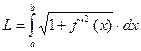или 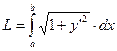(2), где y’=f’(x)

Дифференциал дуги в прямоугольных координатах

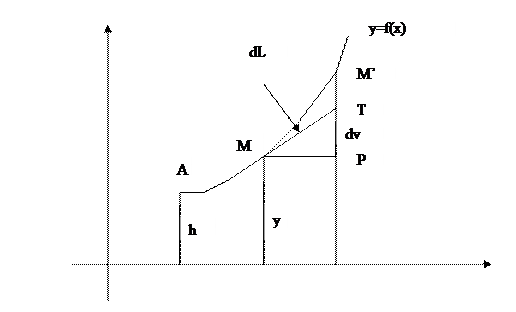
Пусть точка A(a,h) – фиксирована, а точка M(x,y) – переменная. В таком случае длина дуги L=AM есть некоторая функция от х. Согласно (2) имеем 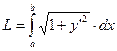Отсюда, используя теорему о производной определенного интеграла с переменным верхним пределом, получим 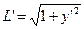и следовательно 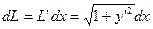, таким образом 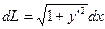- дифференциал дуги в прямоугольных координатах. Так как 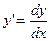, то 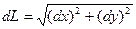(3). Это теорема Пифагора для бесконечно малого треугольника MTP.

Пример

Вычислить длину дуги отрезка цепной линии. Так называется линия, форму которой принимает тяжелая нить, закрепленная в двух точках. Уравнение линии 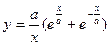(4), где а – параметр цепной линии, а>0. Или проще 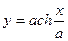(4’) – гиперболический косинус.

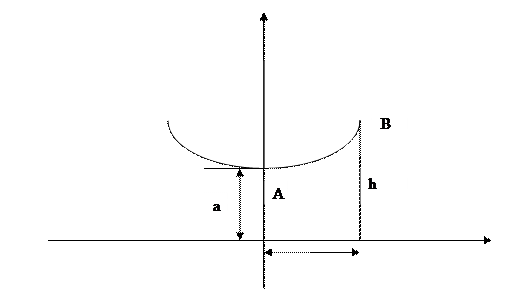
b – абсцисса точки В; h – ордината точки В.

Дифференцируя уравнение (4’) получаем 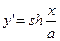. Далее 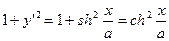. Тогда

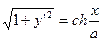. Согласно формулы (2), имеем

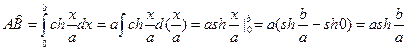
Нахождение длины дуги кривой, заданной параметрическими уравнениями

Пусть L – длина дуги кривой 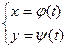, , 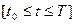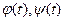- непрерывно дифференцируемые функции на заданном отрезке.

Формула (3) для дифференциала дуги справедлива и в этом случае dx=x’dt; dy=y’dt. Имеем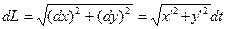

Интегрируя последнее выражение в пределах от 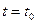до t=T получим длину дуги

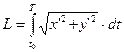(5)

Пример

Найти длину дуги окружности, заданной параметрическими уравнениями

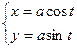от t=0 до t=T

Решение

Здесь dx=-asintdt; dy=acostdt. Поэтому 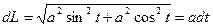и, следовательно

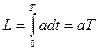
Пример

Найти длину дуги астроиды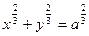

Запишем уравнение астроиды в следующем виде 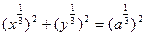. Замена

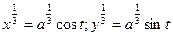. Получаем параметрические уравнения астроиды

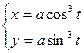
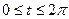(6). Кривая (6) симметрична, поэтому находим 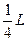при изменении t от 0 до 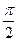. Получаем 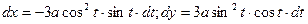. Отсюда

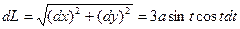. Интегрирую в пределах от t=0 до 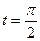, получим

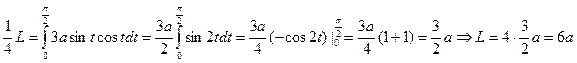
Длина дуги в полярных координатах

Выведем сначала формулу для дифференциала dL дуги в полярных координатах на основании формулы (3)

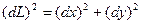, где x,y – прямоугольные декартовы координаты точки дуги.

Формулы перехода:

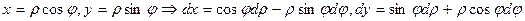
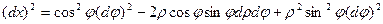
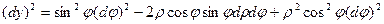
Отсюда 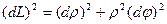, следовательно 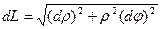или 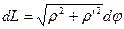(1), где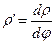

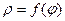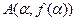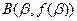Задача Найти длину дуги L непрерывно дифференцируемой кривой между точками и , где 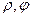- полярные координаты.

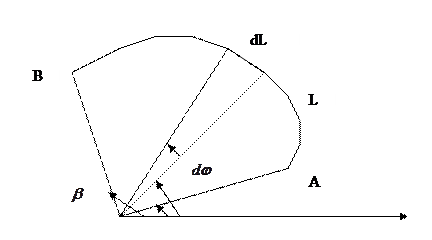
Интегрируя равенство (1) в пределах от 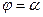до 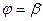получаем длину дуги в полярных координатах

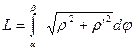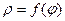,где и 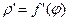- производная

Пример

Вычислить полную длину дуги кардиоиды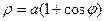

Решение

Имеем 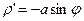, тогда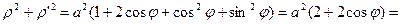

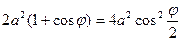,отсюда