Ом және Кирхгоф заңдары комплекстік түрде. Комплексті түрдегі Ом және Кирхгов заңдары

Ом заңы: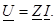

Кирхговтың бірінші заңы: құйынға жалғанған комплексті ток бұтақтарының алгебралық қосындысы, нөлге тең: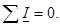

Кирхговтың екінші заңы: тұйық контурдың барлық элементтерінде комплексті кернеудің алгебралық қосындысы нолге тең. Оны басқаша формулаға келтіруге болады: комплексті кернеудің алгебралық қосындысы кез-келген тұйық контурдың элементтерінде осы контурдағы Э.Қ.К. көздерінің кернеулерінің қосындысына тең: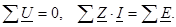

Толық, активті және реактивті қуаттар. Синусоидалы емес токтың активті қуаты барлық гармоникалардың активті қуаттарының қосындысына тең. Толық қуат 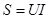- ток пен кернеудің қолданыстағы мәндерінің көбейтіндісімен есептеледі:

.

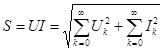Реактивті қуат барлық гармоникалардың реактивті қуаттарының қосындысымен анықталады:

.

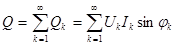1.

2. Кешенді қуат туралы ұғым.

3. Сызықты тізбегтердегі резонанстық құбылыстар.

4. Пассивті екіұштықтардың жиіліктік сипаттамалары.

5. Гармоникалық сигналдың әсері кезіндегі қарапайым және күрделі тізбектерді талдау.

6. Өзара индукция құбылысы.

7. Байланыс коэффициенті.

8. Индуктивті байланысқан шарғыларды бірізді және параллель жалғау.

Үш фазалы электр тізбектері Үшфазалық жүйе - бір электр көзінде индуктелген және бір-бірінен 120⁰ фаза бойынша ауытқитын, бірдей жиілікті синусоидалық ЭҚК жұмыс жасайтын үш электр тізбегінің жиынтығы

Фаза:1)Үшфазалы жүйеге кіретін бірфазалы тізбекті “фаза” деп атау қабылданған

2) Синусоидалық өзгеруші өлшемнің мәнін сол мезетте анықтаушы фазалық бұрыш

9. Сыйымдылық элементтен тұратын сызықты синусоидалық тоқ тізбегі.

10. Күрделі индуктивті байланысқан тізбектерді талдау әдістері

11. Идеалды трансформатор туралы негізгі ұғымдар.

12. Параметрлері таратылған тізбектер туралы ұғымдар

13. Үш фазалы қабылдағышты үш бұрыштар жалғау.

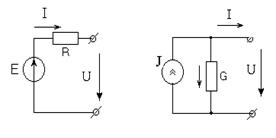
Үш фазалы қабылдағышты жұлдысша схемасы бойынша жалғау Ұшбұрышты кедергінің пайда болуы эквивалентті жұлдызды кедергімен байланысты. Ұшбұрыштың түйіндеріндегі кедергілер R₁, R₂, R₃ эквивалентті үшжарық жұлдыздарды қарастырады.

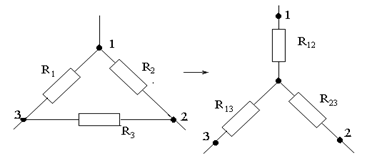Формулалар келесі түрде болады:

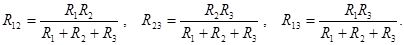
5.Үшжарық жұлдыздың эквивалентті ұшбұрышта пайда болуы.Формулалар келесы түрде болады.

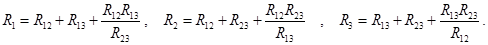
14. Үш фазалы тізбектің симметриялы және симметриялы емес режимдерін есептеу әдістері.

15. Тұрғын толқын.

16. Бұрмаланбаған желі

17. Үш фазалы тізбектің симметриялы және симметриялы емес режимдерін есептеу әдістері

18. . Ток резонансы

19. Біртекті желінің теңдеулері және сипаттамалары

20. Таралу жылдамдығы және толқын ұзындығы.

21. Жиіліктік сипаттамалар.

22. Шығынсыз желі.

23. Кернеу резонансы

24. Үш фазалы тізбектің симметриялы және симметриялы емес режимдерін есептеу әдістері.

25. Үш фазалы тізбектің симметриялы және симметриялы емес режимдерін есептеу әдістері.

26. Үш фазалы тізбектің симметриялы және симметриялы емес режимдерін есептеу

27. әдістері.

28. Үш фазалы тізбектердегі қуаттарды өлшеу

29. Бейсинусоидалы э.қ.к. кернеулер, тоқтар.

30. Бейсинусоидалы шамалардың спектрі.

Өтпелі процесстерді талдау әдістері. Классикадық әдіс. Бірінші дәрежелі тізбектердегі өтпелі процесстер.Өтпелі үрдістерді классикалық әдіспен есептеу

Өтпелі үрдісті классикалық әдіспен есептеу дифференциалды теңдеуді өтпелі үрдіс тізбегінде құралады, бастапқы шарттан тұрақты интегралдауды анықтау және шешу. Өтпелі үрдісті классикалық әдіспен есептеуді тұрақты ЭҚК қорымен тармақталған тізбектегі i₂(t) өтпелі тогын есептеу мысалында қарастырамыз (1.2 сурет).

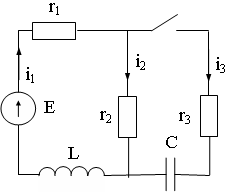
1.2 Сурет

1.1.1 Тәуелсіз бастапқы шарттарды анықтау коммутацияға дейінгі тізбектегі индуктивтіктегі ток i_L(-0) және сыйымдылықтағы кернеу u_C(-0) t= -0 кезінде жүргізіледі

i_L(0)=i₁(0)=i_L(-0)= 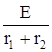, (1.3)

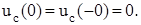
1.1.2 Сипаттамалық теңдеудің түбірлерін анықтау:

- бос құрам үшін дифференциалды теңдеу арқылы сипаттамалық теңдеу құралады;

- комплексті кедергі коммутациядан кейінгі сызбада jw-ны р-ға ауыстыру арқылы өрнек құрастырылады және алынған өрнек нөлге теңестіріледі

,

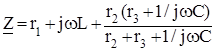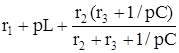=0.

Сипаттамалық теңдеуді түрлендіргеннен кейін аламыз

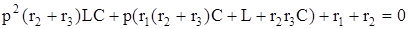(1.4)

(1.4) сипаттамалық теңдеуді шешкенде р-ның түбірін табады.

Сипаттамалық теңдеудің түбірлерінің түрлері бойынша бос құрамды ізделіп отырған шама жазылады. Осыдан үш нұсқа болуы мүмкін (мұнда ток үшін жазылған, кернеу үшін де сол шешулер қолданылады).

а) ақиқат түбірлер (әрдайым теріс), тең емес: р₁¹р₂. Осы жағдайда

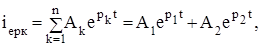
мұнда р_к – к-теңдеу түбірі (1.4);

А_к – белгілі емес тұрақтылар, тұрақты интегралдау болады, ол

біртекті дифференциалды теңдеулерді шешкенде шығады;

к=1 n=1 кезінде және к=1,2 n=2 кезінде;

б)комплексті–түйіндес түбірлер р₁=-a+jw₀,р₂=-a-jw₀.

Осы жағдайда өтпелі үрдістер токтың бос құрамын осылай анықтайды

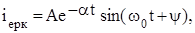
мұнда a, w₀ – оң ақиқат сандар;

a – өшу коэффициенті;

w₀ – контурдың өзіндік тербеліс жиілігі;

А және y - белгісіз константы, әрі қарай шығару жолында

анықталады.

в) тең түбірлер (ақиқат, теріс) р₁ = р₂ = - а.

Онда i_тур = (А₁ + А₂t)е^-at, мұнда А₁ және А₂ – тұрақты белгісіз интегралдаулар.

1.1.3 Өтпелі үрдісте ізденіп отырған токтың i₂(t) өрнегін анықтау

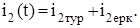
Қалыптасқан режімнің тогін i_2тур өтпелі үрдістен біткеннен кейін аналізден және сұлбаны есептеуден анықтаймыз. Тізбектегі өтпелі үрдісте пайда болады, өйткені конденсатор зарядталады. Сипаттамалы теңдеудің түбірлерімен бос ток анықталады. Бұл жағдайда нақты және тең емес түбірлі бар

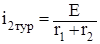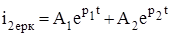, . (1.5)

Өтпелі үрдістің тоғы

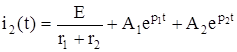. (1.6)

Белгісіз А₁ және А₂ анықтау үшін екі теңдеуді құрастырамыз, i₂(t) өтпелі үрдісте алынған өрнекті дифференциалдаймыз

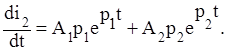(1.7)

1.1.4 Бастапқы шарттан t=0 болғанда, тұрақты интегралдау А₁ және А₂ келесі теңдеу жүйесінен анықтаймыз, (1.6) және (1.7) теңдеулерін қарастырғанда коммутация кезіндегі алынған

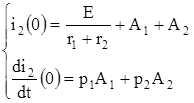. (1.8)

(1.8) теңдеу жүйесін шешу үшін, i₂ токтың мәнін және коммутация кезіндегі оның туындысы (t=0).

1.1.5 i₂(0) және di₂(0)/dt анықтау үшін, бірінші және екінші Кирхгоф заңдары бойынша коммутациядан кейін, қайсысы болсын уақыттын теңдеу жүйесін құрастырамыз

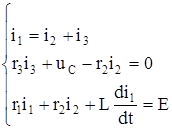. (1.9)

Коммутация кезіндегі (t=0), болғанда бірінші екі теңдеу жүйесін (1.9) жазамыз

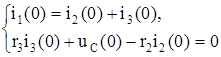. (1.10)

(1.10) жүйеден тәуелсіз бастапқы шартын (1.3) ескеріп, i₃(0) және i₂(0) мәндері анықталады.

(1.9) бірінші және екінші теңдеу жүйелері диффиренцияланады, алынған теңдеу жүйесі t = 0 болғанда жазамыз

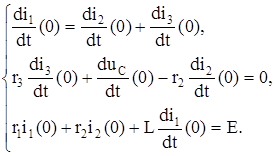(1.11)

(1.11) жүйеден 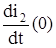мәнін табамыз. Осымен қатар, бұл

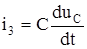, яғни 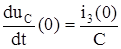. i₃(0) мәнін (1.10) жүйеден табылған.

i₂(0), di₂(0)/dt табылған мәннен (1.8) жүйесіне қоямыз, осыдан тұрақты интегралдау А₁ және А₂ анықталады. А₁, А₂ мәнің қойғаннан кейін (1.6) теңдеуінде өтпелі үрдістің режимінде ізденіп отырған токты i₂(t) табылады.

31. Операторлық беріліс функциялар.

32. Интегралдаушы және дифференциалдаушы тізбектер. Өтпелі және импульстық сипаттамалар. Дюамель интегралы.

33. Периодты емес уақыптық функцияларын Фурье интегралы көмегін көрсету.

34. Комплекс туріндегі Фурье қатары. Жеке импульс спектрі. Жиілік сипаттамалар.

35. Фурье турлендіруінің қасиеттері. Комплекстік беріліс функциясы.

36. Импульс спектріндегі энергияның таралуы.

37. Төртполюстіктер .Электрлік сүзгілер.Негізігі ұғымдар.

Төртұштықтардың негізгі теңдеулері, жалғау және орынбасар схемалары төртұштықтардың жұмыс режимдері, сипаттамалық параметрлері, берілістік функциялары.

Төрт полюстiктiң қасиеттерi коэффициенттермен немесе параметрлермен анықталады. 4 айнымалы дәнекерлiк байланыстар төрт полюстiктiң теңдеулерiмен деп аталады. Төрт полюстiктiң теңдеулерiнiң белгiлi 6 түрлерi, төрт полюстiктiң теңдеулерiнiң 3 түрлерiн бiздiкi қаралады.

Төрт полюстiктердiң теңдеуiн қарап шығамыз. Z - форма, теңдеу параметр арқылы - кедергi:

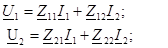
Коэффициенттер төрт полюстiктiң кедергiлерiмен параметрлермен тоқтарда деп аталады.

Матрицалық формада:

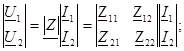
Параметрi төрт полюстiк - бос жүрiстiң кедергiсiнiң параметрлерi. Олар бос жүрiстiң тәртiптерiнен анықталады:

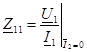— қысқыштардың 1-11, алшақ салынған күйiнделерi бұл төрт полюстiктiң кiретiн кедергiлерi жақтан 2-21,

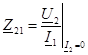— 2-шi 1 кiруге кiруден тiкелей хабар мен бұл берiлiс кедергiлер, және 2-21 тоққа алшақ салынған қысқыштарына кернеудi қатынасы болады.

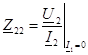— қысқыштардың 2-21, алшақ салынған күйiнделерi төрт полюстiктiң кiретiн кедергiсi жақтан 1-11.

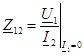— 1-шi 2 кiруге кiруден керi берiлудi 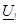берiлiс кедергi, және 1-1¹ 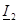тоққа алшақ салынған қысқыштарына қатынасы болады.

Егер тоқтар туралы осы теңдеу шешiлс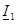е және 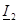, онда аламыз:

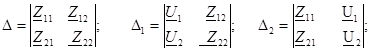
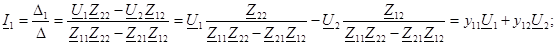
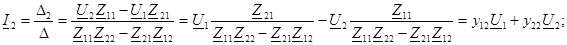
Қасымызда төрт полюстiктiң теңдеуiн сонда аламыз У - формаға:

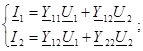
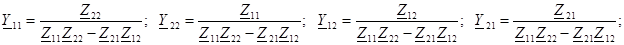
Қасында У - форма, қысқа тұйықталуды өткiзу қабiлетiнiң параметрлерi:

;

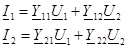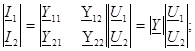
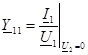- қысқыштар төрт полюстiктiң кiретiн өткiзу қабiлетi жақтан 1-1¹ қысқа тұйықталуда . қысқыштар 2-2¹.

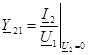-2-шi 1 кiруге кiруден тiкелей хабар мен берiлiс өткiзу қабiлетi, 1-11-шi қысқыштың кернеуiне қысқа тұйықталуды тоқтың қатынасын ұсынады.

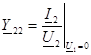-қысқыштар төрт полюстiктiң кiретiн өткiзу қабiлетi жақтан 2-21 1-11ден қысқыштардың қысқа тұйықталуында.

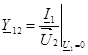-1-шi 2 кiруге кiруден керi берiлудi берiлiс өткiзу қабiлетi, 2-21-шi қысқыштың кернеуiне қысқа тұйықталуды тоқтың қатынасы болады.

3. ( төрт полюстiктiң теңдеуi - формаға) төрт полюстiктiң параметрлерi.

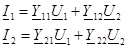
туралы бiрлескен теңдеулердi шешемiз және:

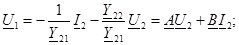
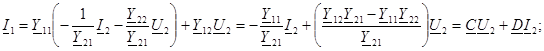
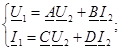
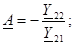
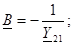
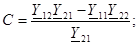
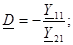
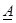- өлшемсiз шама;

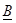– кедергiнiң өлшемi;

– өткiзу қабiлетiнiң өлшемi;

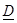– өлшемсiз шама.

Теңдеулер А - формаға матрицалық формада жазып алуға болады:

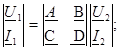
Коэффициенттер керi қоректенуде А және D ауысады және төрт полюстiктердiң теңдеуi пайда болады В - формаға:

.

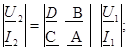
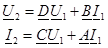Егер қоректену көзiнде және жүктемеге қоректену көзi және жүктеменiң орындарымен өзгерiске, тоқтар бұлжымаса төрт полюстiк симметриялық деп аталады. 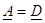симметриялық төрт полюстiкке. Егер 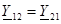, онда төрт полюстiк өзара деп аталады.

Өзаралықтар шарт 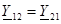жеткiлiктi төрт полюстiктер үшiн:

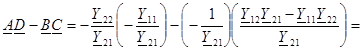
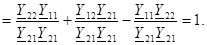
Жүктеменiң жанында төрт полюстiктiң тәртiбi. Теңдеулердiң әр түрлi түрлерiнiң қолдануымен жұмыс тәртiптерi есептеуде тоқтардың бағытының жағдайы алажаулы таңдалуға қабылдалған. Тоқтардың оң бағыттары суретте көрсетiлген.

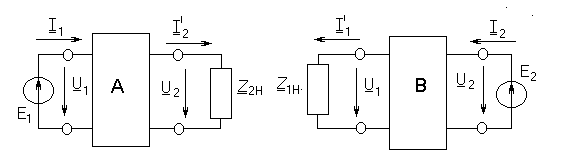
Төрт полюстiктiң жұмыс тәртiптерi мiнездемеге 1-1¹-шi жақтан алғашқы қысқыштардың кiретiн кедергiсiнiң ұғымдарымен жиi пайдаланады, 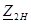жүктеменiң кедергiсiнде және 2-2¹-шi жақтан екiншi қысқыштардың кiретiн кедергiсiнiң ұғымымен, 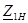жүктеменiң кедергiсiнде. 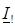тоққа 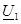кернеудi қатынас жақтан алғашқы қысқыштардың төрт полюстiгiнiң қоректенуi және жақтан екiншi қысқыштардың жүктемесiнiң кедергiсiнде, жақтан алғашқы жадағайлалардың кiретiн кедергiсiмен деп аталады: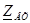

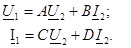
Кiретiн кедергiнiң анықтаулары үшiн жеткiлiктi

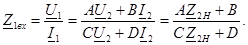
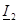тоққа 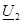кернеудi қатынас жақтан екiншi жадағайлалардың кiретiн кедергiсiмен жақтан екiншi қысқыштардың төрт полюстiгiнiң қоректенуi және жақтан алғашқы қысқыштардың 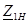жүктемесiнiң кедергiсiнде деп аталады.

Керi берiлудiң жанында дәл осылай:

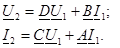
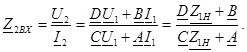
Төрт полюстiктiң кiретiн кедергiсi қоректену көзiнiң жұмыс тәртiбiн анықтайды және параметрлерiнiң элементтердiң төрт полюстiк құрайтын құрылымдарынан тәуелдi болады, яғни қабылдағыштың кедергiсi, яғни төрт полюстiктiң коэффициенттерi, сонымен бiрге жүктеменiң кедергiсiнен. Анықтаулар үшiн 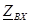теңдеулер түрлердiң қайсысы болса да пайдалануға болады, яғни тек қана оның коэффициенттерiнен тәуелдi болады, дегенмен өрнектiң бос тұрулары өте А және В ның формаларында пайда болады және айырылған күйiнде немесе кiретiн кедергi тұйықтандырылған қабылдағыш жағдай бөлiндiде тек қана өзiмнiң төрт полюстiгiн мiнездейдi.

1 ) жақтан алғашқы қысқыштардың қоректенуi, екiншi қысқыштардың қысқа тұйықталуы:

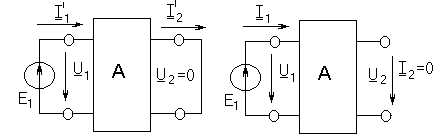
бос жүрiс қысқа тұйықталу

Қысқа тұйықталулардың жанында: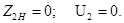

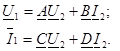
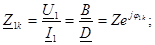
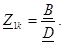
2. Екiншi қорытындыларға бос жүрiсi: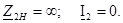

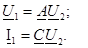
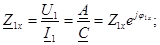
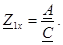
3. Жақтан екiншi қысқыштардың қоректенуiнде, алғашқы қысқыштардың қысқа тұйықталуы.

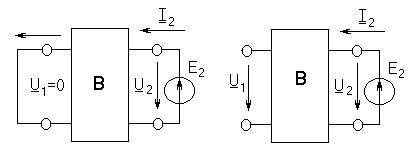
бос жүрiс қысқа тұйықталу

Қысқа тұйықталулардың жанында: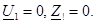

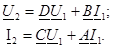
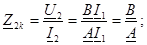
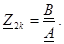
2. Екiншi қорытындыларға бос жүрiсi:

Бос жүрiстердiң жанында:

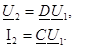
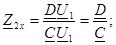
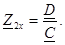
Қысқа тұйықталу және төрт полюстiктiң бос жүрiсiнiң кедергiлерi оның коэффициенттерiмен анықталады.

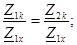
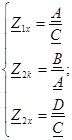
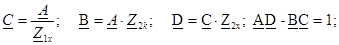
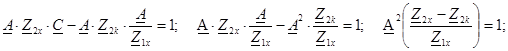
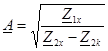
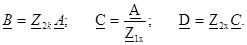
Төрт полюстiктiң теңдеулерi А - формаға:

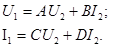
керi берiлу

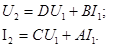
Төрт полюстiктердiң параметрлерiнiң эксперименталдi анықтауы

Пассивтi төрт ұштықтарды кешендi коэффициенттер тәжiрибелi жолымен немесе есептеулермен анықталады. Анықтаулар үшiн, тәжiрибелi жолымен А, В, С, D екi тәжiрибелердiң мәлiметтерi алуға жеткiлiктi: бос жүрiс және қысқа тұйықталулар.

1. Бос жүрiстiң тәжiрибесi, алғашқы параметрлердiң 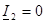алшақ салынған қоректенулерi 2-2¹:

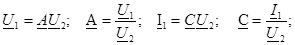
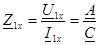-- 1-1¹-шi жақтан алғашқы қысқыштардың кiретiн кедергiсi.

2. Жақтан алғашқы қысқыштардың қысқа тұйықталуды тәжiрибе, 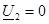қоректенуi, 2-2 - қысқа тұйықталу:

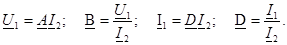
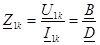- жақтан 1-1¹-шi кiретiн кедергi, 2- 2¹ қысқа тұйықталуда.

38. Төртұштықтардың есептеу жолы.

39. Электрлік сүзгілердің негізігі ұғымдары және түсініктемелер.

40. «К» типті төменгі жиіліктік, жоғары жиіліктік, алқапты, бөгеуіштік және көпір сүзгілердің жұмыстары, орынбасар схемалары.

41. «m» типті сүзгілер туралы ұғымдар.

42. Индукциясыз сүзгілер.

43. Бейсинусоидалық шамалардың максималь мәні

44. Бейсинусоидалық шамалардың әсер мәні .Өтпелі процесстің пайда болу шарттары
Коммутацияның бірінші заңы. Коммутацияның екінші заңы

45. Электр тізбектерінің ауыспалы және импульсті сипаттамасы. Дюамель интегралы Ауыспалы процесстерді талдауға кажет шарттар:

46. Ауыспалы процесті классикалық әдіспен есептеудің . алгоритмі

47. Сүзгілердің өткізу сппектріне қарай бөлінуі

86.Сүзгілердің параметрлері