Примеры. 1. Найти уравнения касательной плоскости и нормали:

1. Найти уравнения касательной плоскости и нормали:

а) к поверхности 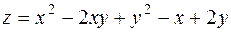в точке М(1, 1, 1).

Находим частные производные и их значения в указанной точке касания:

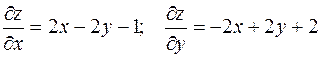
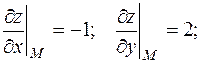
На основе формул (1) и (2) составим уравнения касательной и нормали.

Уравнение касательной плоскости:

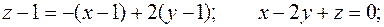
Уравнение нормали:

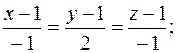
б) к эллиптическому параболоиду 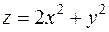в точке .

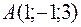Преобразуем уравнение поверхности к виду: .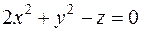

И, обозначив его левую часть через 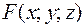, найдем частные производные:

, , .

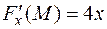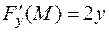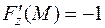Вычислим их числовые значения в указанной точке :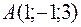

, , .

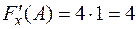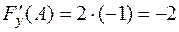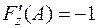Подставляя найденные значения в общие уравнения (3) и (4), получим

- уравнение касательной плоскости:

.

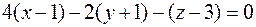- уравнение нормали к поверхности в этой точке:

.

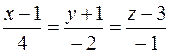2. На сфере 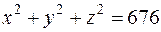найти точки, где касательная параллельна плоскости .

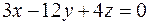1) Пользуясь общим уравнением (3), составим уравнение касательной плоскости к данной сфере в ее точке 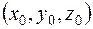(координаты которой нам нужно найти):

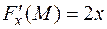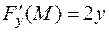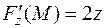, , - частные производные уравнения сферы.

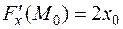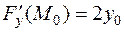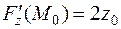, , - их значения в точке касания. Отсюда:

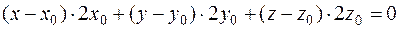
Сократив выражение на 2, и раскрыв скобки, получим:

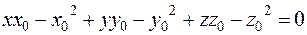
или .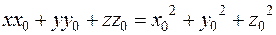

2) Точка сферы 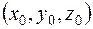должна удовлетворять ее уравнению 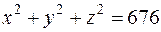. Это означает, что 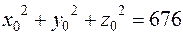. Следовательно,

.

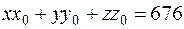3) Воспользуемся условием параллельности искомой касательной к заданной плоскости. Согласно условию параллельности двух плоскостей, коэффициенты при текущих координатах этих плоскостей должны быть пропорциональны:

.

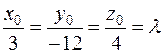Запишем последние равенства в виде системы уравнений:

(*)

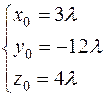4) Подставим найденные в параметрическом виде (*) координаты точек сферы в ее уравнение:

,

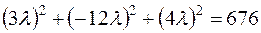откуда находим, что .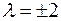

5) Подставляя найденные числовые значения 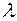в (*), найдем координаты искомых точек, в которых касательная плоскость параллельна заданной плоскости:

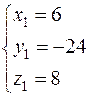и .

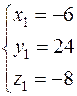3. Показать, что касательные плоскости к поверхности 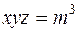образуют с координатными плоскостями тетраэдр постоянного объема.

Уравнение касательной плоскости к данной поверхности в точке 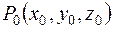имеет вид:

.

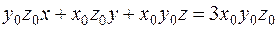Эта плоскость на координатных осях отсекает отрезки:

, , .

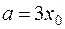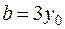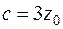Перечисленные отрезки являются взаимно перпендикулярными ребрами тетраэдра, образованного касательной плоскостью и координатными плоскостями. Приняв одно из этих ребер за высоту тетраэдра, найдем, что его объем

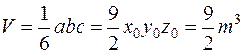, так как точка 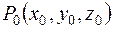лежит на данной поверхности. Причем объем не зависит от координат точки касания. Из этого следует, что различные касательные плоскости к данной поверхности образуют с плоскостями координат тетраэдр постоянного, равного, объема.

11. Экстремумы функции нескольких переменных

11.1 Локальный экстремум

Локальный экстремум (т.е. максимум или минимум) для ФНП определяется так же, как и для функции одной переменной.

1°. Функция 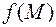, определенная в некоторой области, имеет локальный максимум в точке 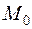, если в некоторой окрестности этой точки верно неравенство:

,

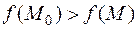и локальный минимум, если выполняется неравенство:

.

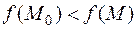Очевидно, что в окрестности точки экстремума 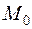приращение функции

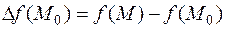
сохраняет знак, а именно:

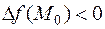, если 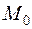- точка максимума

и 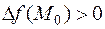, если 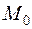- точка минимума.

Для исследования функции на экстремум применяют следующие теоремы.

Теорема 1. (Необходимые условия экстремума). Функция нескольких переменных 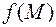может иметь экстремум только в точках, лежащих внутри области определения функции, в которых все частные производные первого порядка одновременно равны нулю или не существуют.

Такие точки будем называть критическими точками.Точки, в которых все частные производные первого порядка одновременно равны нулю, - стационарными.

Не всякая критическая точка является точкой экстремума. Другими словами, необходимый признак существования экстремума не является достаточным.

Например, для функции 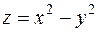ее частные производные 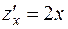и 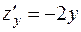одновременно обращаются в нуль в точке О(0, 0), но:

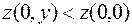, а ,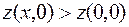

поэтому в точке О(0, 0) экстремума нет.

Таким образом, для исследования функции на экстремум нужно:

1) найти критические точки (в которых все частные первого порядка одновременно обращаются в нуль или не существуют)

2) исследовать функцию в критических точках, используя достаточные признаки экстремума или определение экстремума (исследование знака приращения функции в критической точке).

Теорема 2. (Достаточные признаки экстремума для функции двух переменных).

Пусть 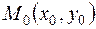- критическая точка функции 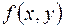, а сама функция дважды дифференцируема в критической точке. Обозначим:

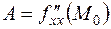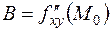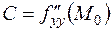, , и .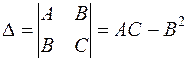

Тогда

1) если определитель 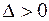, то 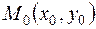- точка экстремума, причем если

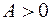- то точка минимума

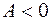- точка максимума:

2) если определитель 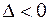, то функция экстремума в данной точке не имеет;

3) если определитель 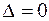, то для решения вопроса о наличии или отсутствии экстремума в точке 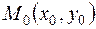требуются дальнейшие исследования, например, по знаку приращения функции 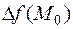вблизи этой точки.