Дополнительные задачи по графам
Решение
1) Базис индукции. При 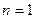 формула верна, так как
формула верна, так как 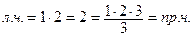
2) Индукционный шаг. Пусть 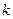 — произвольное натуральное число и формула справедлива при
— произвольное натуральное число и формула справедлива при 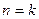 , т. е.
, т. е.
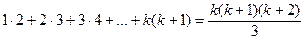 .
.
Докажем, что тогда формула имеет место и при 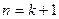 , т.е.
, т.е.
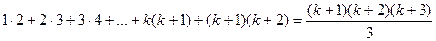 Действительно,
Действительно,
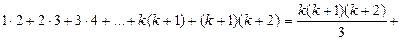
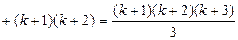 .
.
Следовательно, формула справедлива при всех натуральных 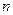 .
.
Пример 2. Доказать, что при всяком натуральном 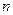 число
число 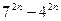 делится на
делится на 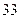 .
.
Доказательство проведем методом математической индукции.
1) Базис индукции. При 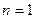 утверждение справедливо, так как
утверждение справедливо, так как 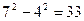 делится на
делится на 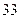 .
.
2) Пусть 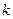 — некоторое натуральное число и утверждение справедливо при
— некоторое натуральное число и утверждение справедливо при 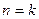 , то есть
, то есть 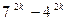 делится на 33.
делится на 33.
Докажем,что тогда утверждение справедливо для следующего натурального числа 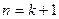 , то есть докажем, что
, то есть докажем, что 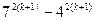 делится на 33.
делится на 33.
Действительно, 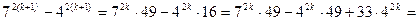
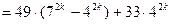 делится на 33, так как первое слагаемое
делится на 33, так как первое слагаемое 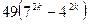 делится на 33 в силу предположения и
делится на 33 в силу предположения и 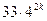 , очевидно, делится на 33. Следовательно,
, очевидно, делится на 33. Следовательно, 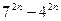 делится на 33 при любом натуральном
делится на 33 при любом натуральном 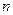 .
.
Задачи
1.Докажите методом математической индукции, что для всех натуральных 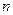
1). 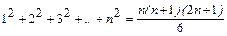 .
.
2). 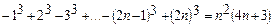 .
.
3). 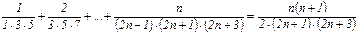 .
.
2.Докажите методом математической индукции, что для всех натуральных 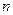
1). 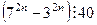 .
.
2). 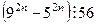 .
.
3). 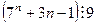 .
.
4). 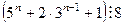 .
.
5). 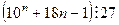 .
.
3. Докажите, что
1). 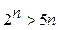 при
при 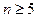 .
.
2). 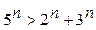 при
при 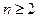 .
.
3). 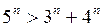 при
при 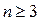 .
.
4). 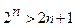 при
при 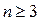 .
.
Домашнее задание
Основные задачи
Докажите методом математической индукции, что для любого натурального числа 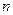
1) 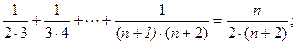
2) 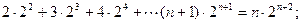
3) 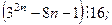
4) 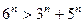 при
при 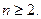
Дополнительные задачи
1) Докажите, что при нечетном 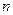
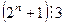 .
.
2) Найдите сумму 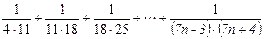 .
.
3) Докажите, что 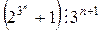 .
.
4) Докажите, что 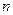 окружностей, лежащих в одной плоскости, разбивают эту плоскость на области, которые можно закрасить белой и черной красками так, что все смежные области (т.е. области, имеющие общую границу) будут закрашены разными красками (белой и черной).
окружностей, лежащих в одной плоскости, разбивают эту плоскость на области, которые можно закрасить белой и черной красками так, что все смежные области (т.е. области, имеющие общую границу) будут закрашены разными красками (белой и черной).
5). Докажите формулу для последовательности Фибоначчи:
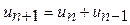 1, 1, 2, 3, 5, 8,…
1, 1, 2, 3, 5, 8,…
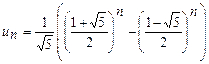 .
.
6). Найдите сумму 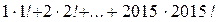 .
.
2. КОМБИНАТОРИКА. ОСНОВНЫЕ ПРАВИЛА КОМБИНАТОРИКИ
Соединения без повторений
1. На одном из дорожных указателей стояло: «Аркаим 20 км». Вскоре путешественник понял, что на указателе или первая, или последняя цифра (только одна) была стерта. а). Сколько вариантов дорожного указателя могло быть? б). Тот же вопрос при 22 км.
2. Если авиакомпания осуществляет 15 рейсов из Сан-Франциско в Чикаго и 20 рейсов из Чикаго в Нью-Йорк, то сколько всего рейсов из Сан-Франциско в Нью-Йорк проходит транзитом через Чикаго?
3. В меню университетской столовой имеется 4 первых, 5 вторых и 3 третьих блюда. Сколькими способами можно выбрать обед а) только из одного блюда, б) одного первого, одного второго и одного третьего блюда, в) только из двух блюд, г) хотя бы из одного блюда?
4. Сколько существует пятизначных натуральных чисел, в каждом из которых все цифры различны?
5. Сколько существует пятизначных натуральных чисел, в каждом из которых соседние цифры различны?
6. Сколько существует шестизначных натуральных чисел, в каждом из которых нет одинаковых цифр, а вторая и четвертая цифры нечетные?
7. Сколько существует пятизначных натуральных чисел, в записи которых есть хотя бы одна четная цифра?
8. Сколько существует натуральных чисел между 0 и 1000, содержащих хотя бы одну цифру 7?
9. Сколько существует пятизначных натуральных чисел, начинающихся с двух одинаковых цифр?
10. Сколько существует пятизначных нечетных натуральных чисел, в каждом из которых все цифры различны?
11. Сколько существует различных шестизначных телефонных номеров, состоящих из различных цифр?
12. Сколько различных натуральных делителей имеет число 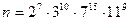 ?
?
13. Сколькими способами можно разместить на полке 5 из 8 различных книг?
14. Сколькими способами можно распределить 25 заданий между 25 студентами?
15. Сколькими способами можно рассадить 10 студентов в аудитории на 24 места?
16. Итальянский город Падуя характеризуется тремя фразами вида «А без В», где А и В — разные слова из множества 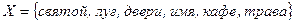 . Сколько разных характеристик можно составить?
. Сколько разных характеристик можно составить?
17. В группе из 10 юношей и 15 девушек нужно выбрать делегацию из 5 человек. Сколькими способами это можно сделать, если а) выбираются 2 юноши и 3 девушки, б) должны быть выбраны хотя бы две девушки?
Домашнее задание
1. Сколькими способами можно выбрать гласную и согласную буквы в слове а) портал, б) занятие?
2. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского, на любой другой из этих пяти языков?
3. У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?
4. Найдите 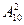 ,
, 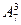 ,
, 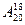 ,
, 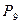 ,
, 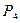 ,
, 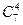 ,
, 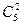 ,
, 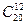 .
.
5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если ни одна цифра не должна повторяться?
6. Сколькими способами можно выбрать три краски из имеющихся пяти?
7. Сколькими способами можно выбрать 5 человек в группе из 20 человек?
8. Сколькими способами можно выпустить хоккейную команду на площадку, имея трех вратарей, 5 защитников и 6 нападающих?
9. В первенстве страны по футболу участвуют 16 команд. Сколькими способами могут распределиться 3 медали (золотая, серебряная, бронзовая)?
10. В аудитории имеется 10 лампочек. Сколько существует разных способов ее освещения, при которых горит ровно 3 лампочки?
11. В группе из 15 студентов нужно выбрать троих для поездки в Аргентину. Сколькими способами это можно сделать?
12. В группе из 15 студентов нужно выбрать троих для продолжения учебы во Франции, Англии и США. Сколькими способами это можно сделать?
13. Из 10 экономистов и 7 бухгалтеров необходимо составить комиссию из 3 экономистов и двух бухгалтеров. Сколькими способами это можно сделать?
14. Сколько существует шестизначных чисел, в каждом из которых нет одинаковых цифр, а вторая и четвертая цифры четные?
15. Студенты ходят на занятия нерегулярно. Может прийти вся группа в 20 человек, может кто-нибудь один не прийти, или двое, или трое,…, может даже случится так, что никто не придет на занятия. Сколько различных составов может собраться на занятии?
16. Сколькими способами можно рассадить 12 человек за столом а) без каких либо ограничений; б) так, чтобы Ваня сидел рядом с Таней?
17. Сколькими способами можно расставить 20 различных книг на полке
а) без каких либо ограничений; б) так, чтобы 3 тома трехтомника Стругацких стояли рядом; в) чтобы эти 3 тома стояли рядом, причем в порядке возрастания номеров; г) чтобы эти 3 тома стояли в порядке возрастания, хотя и необязательно рядом?
18. Докажите свойства сочетаний
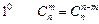 ,
,
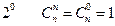 ,
,
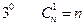 ,
,
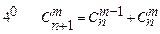 .
.
19. В классе 15 мальчиков и 15 девочек. Сколькими способами можно рассадить их за 15 партами так, чтобы за каждой партой мальчик сидел слева, а девочка справа?
20. В классе 15 мальчиков и 15 девочек. Сколькими способами можно рассадить их за 15 партами так, чтобы каждый мальчик сидел рядом с девочкой?
21. В классе 15 мальчиков и 15 девочек. Сколькими способами их можно разбить на пары танцевать вальс на вечере?
Соединения с повторениями
1. Найдите а) седьмой член разложения 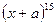 , б) третий член разложения
, б) третий член разложения 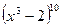 .
.
I. Размещения с повторениями
2. n-мерным двоичным вектором или битовой строкой длины n называется упорядоченный набор из n элементов, каждый из которых может быть 0 или 1. Сколько существует различных а) пятимерных двоичных векторов, б) двоичных векторов длины n?
3. На множестве пятимерных двоичных векторов зададим функции, принимающие только значения 0 и 1. Сколько различных функций такого вида существует?
4.. В языке племени ням-ням существует всего 3 буквы. Сколько различных четырехбуквенных слов может существовать в языке этого племени?
II. Перестановки с повторениями
5. Сколькими способами можно переставить буквы в слове а) сон, б) око?
6. Сколькими способами можно переставить буквы в слове а) арбуз (сумка, пакет), б) короб (молот, болото), в) коробок (водопровод, колокольчик) г) абракадабра?
7. Сколькими способами можно составить шестизначное число, в запись которого входят 2 двойки и 4 четверки?
8. Сколькими способами можно расселить 8 студентов по трем комнатам: одноместной, трехместной и четырехместной?
9. В студенческой группе, состоящей из 25 человек, при выборе старосты за выдвинутую кандидатуру проголосовало 12 человек, против — 10, воздержалось 3. Сколькими способами могло быть проведено такое голосование?
10. Сколькими способами можно раскрасить в красный, синий и зеленый цвет по два разных предмета?
11. Сколькими способами можно распределить 20 различных предметов между пятью лицами так, чтобы каждый получил по четыре предмета?
12. Экскурсанты заказали 5 четырехместных кают на теплоходе. Все места в каждой из кают и все каюты равноценны. Сколькими способами это можно сделать?
III. Сочетания с повторениями
13. В книжном магазине имеется 8 разных подарочных изданий в большом количестве. Сколькими способами можно купить 11 таких книг?
14. В буфете имеются в большом количестве пирожки 5 видов. Сколькими способам можно купить 10 пирожков, если а) покупать можно и одинаковые пирожки, б) нужно купить хотя бы по одному пирожку каждого вида? Как изменится ответ, если пирожки покупаются 10-ю студентами?
15. Сколькими способами 10 одинаковых шаров можно разложить по 5 различным ящикам?
16. Сколькими способами 5 пиратов могут разделить между собой 10 монет, если а) допускаются все способы дележа, б) каждый должен получить хотя бы по одной монете?
17. Садовнику необходимо высадить в течение недели 100 одинаковых саженцев. Сколькими способами он может это сделать, если а) каждый день надо садить хотя бы один, б) он может устраивать выходные?
Домашнее задание
1. Найдите а) девятый член разложения 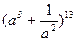 ; б) седьмой член разложения
; б) седьмой член разложения 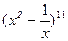 .
.
2. В буфете продается много пирожных каждого из четырех видов. Сколькими способами можно купить 7 пирожных, если а) покупать можно и одинаковые пирожные; б) нужно купить хотя бы по одному пирожному каждого вида?
3. Сколько разных слов можно составить, переставляя буквы в словах а) корвет, б) математика, в) околоток?
4. Сколькими способами можно переставить буквы в слове «огород», чтобы 3 буквы «о» не шли рядом?
5. Государственный совет Швамбрании подал в отставку. Предстоит формирование нового совета из 7 человек, причем в него могут быть избраны представители 4 политических партий Желтой, Оранжевой, Синей и Фиолетовой. Сколько разных советов можно составить, если иметь в виду только численное представительство партий?
6. Сколько существует прямоугольных параллелепипедов, измерения которых являются целыми числами от 5 до 14?
7. Сколькими способами можно группу из 20 человек разбить на две подгруппы по 10 человек для практических занятий, если а) занятия ведет один преподаватель; б) занятия ведут два разных преподавателя?
8. Сколькими способами можно группу из 20 человек разбить на четыре подгруппы по 5 человек?
9. В некотором государстве не было двух жителей с одинаковым набором зубов. Какова может быть наибольшая численность населения государства (наибольшее число зубов равно 32)?
10. Сколько решений в натуральных числах имеет уравнение 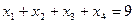 ?
?
11. Сколько решений в неотрицательных целых числах имеет уравнение 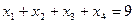 ?
?
12. Сколькими способами можно раздать 18 различных призов 5 участникам так, чтобы а) четверо из них получили по четыре приза, а пятый два, б) трое получили по четыре приза, а двое—по три?
Дополнительные задачи
13. Пусть словом считается любая последовательность из четырех букв. Сколько слов можно составить из букв слова а) караван, б) катапульта?
14. На плоскости проведены 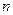 попарно пересекающихся прямых, среди которых нет ни одной тройки пересекающихся в одной точке. Найдите число точек пересечения этих прямых.
попарно пересекающихся прямых, среди которых нет ни одной тройки пересекающихся в одной точке. Найдите число точек пересечения этих прямых.
15. Известно, что никакие три диагонали выпуклого 12-угольника не пересекаются в одной точке. Найдите число точек пересечения диагоналей.
16. Найдите количество 2015–значных чисел, каждое из которых содержит все цифры, кроме 0, и никакие две рядом стоящие цифры которых не являются одинаковыми.
17. Найдите коэффициент при 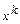 в разложении по степеням
в разложении по степеням 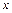 выражения
выражения 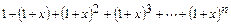 .
.
3. МНОЖЕСТВА
Домашнее задание
1. Найдите 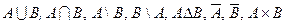 , если
, если
а) 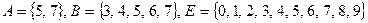 ;
;
б) 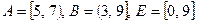 .
.
2. Докажите равенства взаимным включением
а) 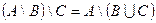 ,
,
б) 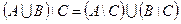 ,
,
в) 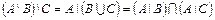 .
.
3. В группе из 25 студентов 17 человек сдали экзамен по дискретной математике, 21 — по линейной алгебре, оба экзамена сдало 15 человек. Сколько человек не сдало ни одного из этих экзаменов?
4. На вершину Пилатуса можно подняться по подвесной канатной дороге, по зубчатой железной дороге или пешеходными тропами. Каждый из 45 туристов попробовал хотя бы один из этих способов, при этом 29 проехали по зубчатке, 29 — по канатной дороге, 11 ходили пешком; 18 попробовали и зубчатку, и канатную дорогу, 4 — канатную дорогу и пешеходные тропы, 3 — зубчатку и пешеходные тропы. Сколько человек попробовали все три способа, а сколько предпочли только пешеходные прогулки?
5. Определите виды отношений
I. 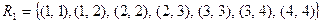
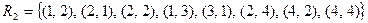
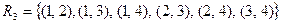 на
на 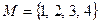 .
.
II. 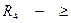 ,
, 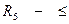 ,
, 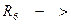 ,
, 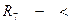 на R.
на R.
III. 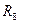 — знакомства,
— знакомства, 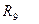 — родства,
— родства, 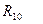 — любви,
— любви,
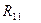 — учиться в одной группе,
— учиться в одной группе, 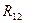 — быть старше,
— быть старше,
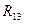 — быть тезками на множестве людей.
— быть тезками на множестве людей.
IV. 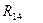 — деления на N.
— деления на N.
Постройте графы и матрицы для отношений 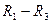 .
.
6. Отношение 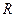 из
из 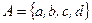 в
в 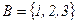 задано матрицей
задано матрицей 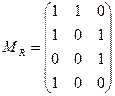 . Запишите элементы множества
. Запишите элементы множества 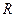 и постройте двудольный граф отношения.
и постройте двудольный граф отношения.
7. Придумайте задачу на пересечения трех множеств. Запишите задачу и ее решение на отдельном листе.
Дополнительные задачи
8. Дом детского творчества регулярно посещают 220 школьников. При доме имеется 6 спортивных секций: легкоатлетическая (л), волейбольная (в), баскетбольная (б), футбольная (ф), секция самбо (с) и шахматная (ш). Число участников этих секций таково: (л) — 30 человек, (в) — 26 человек, (б) — 32 человека, (ф) — 31 человек, (с) — 28 человек, (ш) — 36человек. Несколько секций посещают 53 школьника; из них:24 школьника посещают 3 или более секций, 9 школьников не меньше — четырех секций и 3 школьника — даже 5 секций (в последнюю тройку школьников входит и один чудак, который посещает все 6 спортивных секций). Сколько из посещающих дом детского творчества школьников не участвуют ни в одной спортивной секции?
9. (Задача Льюиса Кэрролла) В ожесточенном бою 70 из 100 пиратов потеряли один глаз, 75 — одно ухо, 80 — одну руку и 85 – одну ногу. Каково минимальное число потерявших одновременно глаз, ухо, руку и ногу?
10. Коля, Вова и Саша решили вместе 100 задач. Каждый мальчик решил по 60 задач. Назовем задачу легкой, если ее решили все три мальчика, и трудной, если ее решил только один мальчик. Докажите, что трудных задач было на 20 больше, чем легких.
11. Петя собирается все 90 дней каникул провести в деревне и при этом строго придерживаться такого распорядка: каждый второй день (т.е. через день) ходить купаться на озеро, каждый третий ездить в магазин за продуктами, каждый пятый день решать задачи по математике. В первый день Петя проделал и то, и другое, и третье и очень устал. Сколько будет у Пети «приятных» дней, когда нужно будет купаться, но не нужно будет ездить в магазин и решать задачи, а сколько «скучных», когда не будет никаких дел?
4. ОТНОШЕНИЯ И ОПЕРАЦИИ НА МНОЖЕСТВАХ
Домашнее задание
1. Отношение эквивалентности на множестве 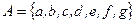 задано разбиением на классы эквивалентности
задано разбиением на классы эквивалентности 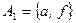 ,
, 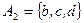 и
и 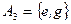 . Представьте это отношение множеством упорядоченных пар, матрицей и графом.
. Представьте это отношение множеством упорядоченных пар, матрицей и графом.
2. Сколько существует всевозможных отображений множества 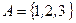 в
в 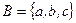 . Выпишите сюръективные отображения. Выясните, будут ли они инъективными и биективными.
. Выпишите сюръективные отображения. Выясните, будут ли они инъективными и биективными.
3. Для основных элементарных функций укажите множества, между которыми они устанавливают взаимно однозначное соответствие.
4. Установите взаимно однозначное соответствие между числовыми промежутками 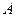 и
и 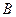 аналитически, если
аналитически, если 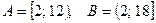 .
.
5. На множестве 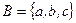 бинарная операция
бинарная операция 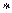 задана таблицей Кэли
задана таблицей Кэли
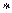 | 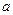 | 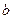 | 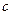 |
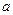 | 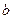 | 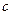 | 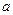 |
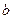 | 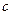 | 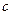 | 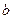 |
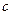 | 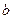 | 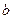 | 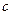 |
Проверьте, будет ли эта операция коммутативной, ассоциативной.
6. Проверьте, можно ли на множестве матриц третьего порядка вида 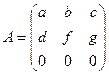 рассматривать операцию произведения матриц.
рассматривать операцию произведения матриц.
Дополнительные задачи
7. Установите взаимно однозначное соответствие между точками отрезка 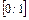 и интервала
и интервала 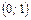 .
.
8. Докажите, что множество точек квадрата 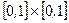 имеет мощность континуума.
имеет мощность континуума.
5. АЛГЕБРЫ, ПОЛУГРУППЫ, ГРУППЫ
1. Преобразование конечного множества 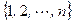 можно задать в следующем виде:
можно задать в следующем виде: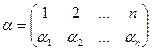 ,имея в виду, что
,имея в виду, что 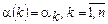 . Композицию двух преобразований
. Композицию двух преобразований 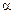 и
и 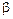 будем обозначать
будем обозначать 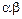 . Пусть
. Пусть 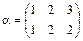 ,
, 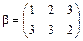 , тогда
, тогда 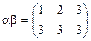 ,
, 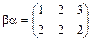 и
и 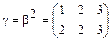 ,
, 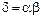 ,
, 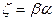 .
.
Составьте таблицу Кэли для операции композиции на множестве 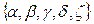 и докажите, что оно образует полугруппу (без единицы). Что можно взять в качестве единицы? Получится ли группа с добавлением единицы?
и докажите, что оно образует полугруппу (без единицы). Что можно взять в качестве единицы? Получится ли группа с добавлением единицы?
2. Является ли булева алгебра 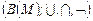 полугруппой, группой по отношению к каждой из своих операций?
полугруппой, группой по отношению к каждой из своих операций?
3. Докажите, что пары чисел 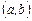 с
с 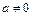 составляют группу относительно умножения
составляют группу относительно умножения 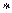 , определенного формулой
, определенного формулой 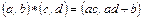 .
.
4. Докажите, что линейные функции 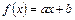 ,
, 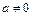 образуют группу относительно операции композиции, изоморфную группе примера 3.
образуют группу относительно операции композиции, изоморфную группе примера 3.
5. Докажите, что пары чисел 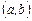 с
с 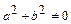 составляют группу относительно умножения
составляют группу относительно умножения 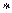 , определенного формулой
, определенного формулой 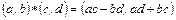 .
.
Домашнее задание
6. Для группы подстановок на множестве 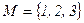 составьте таблицу Кэли. Определите обратный для каждого элемента
составьте таблицу Кэли. Определите обратный для каждого элемента 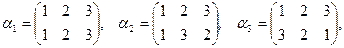
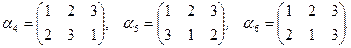
7. Докажите, что множество 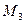 квадратных матриц третьего порядка образует полугруппу относительно операции умножения матриц.
квадратных матриц третьего порядка образует полугруппу относительно операции умножения матриц.
Рассмотрим а) 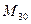 — подмножество
— подмножество  матриц с последней нулевой строкой, б)
матриц с последней нулевой строкой, б) 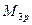 — подмножество
— подмножество 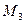 матриц, все элементы которых равны между собой. Образуют ли эти множества полугруппы, группы относительно операции умножения?
матриц, все элементы которых равны между собой. Образуют ли эти множества полугруппы, группы относительно операции умножения?
8. Дана группа 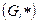 относительно операции, заданной таблицей Кэли
относительно операции, заданной таблицей Кэли
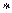 | 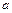 | 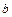 | 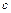 | 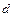 | 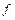 | 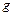 |
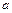 | 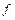 | 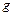 | 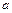 | 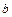 | 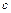 | 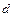 |
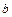 | 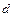 | 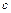 | 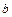 | 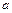 | 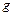 | 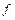 |
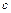 | 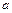 | 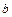 | 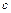 | 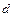 | 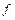 | 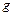 |
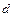 | 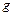 | 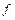 | 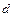 | 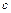 | 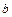 | 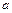 |
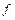 | 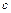 | 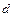 | 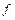 | 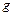 | 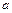 | 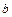 |
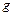 | 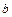 | 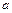 | 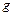 | 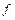 | 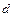 | 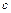 |
1). Является ли группа абелевой?
2). Какой элемент играет роль единичного?
3). Для каждого элемента найдите обратный.
4). Вычислите 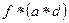 .
.
5). Покажите, что множества 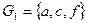 и
и 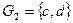 образуют подгруппы относительно данной операции.
образуют подгруппы относительно данной операции.
6. ГРАФЫ
Задача 1.Дан граф.
1. Составьте таблицу степеней 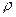 и
и 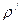 всех вершин графа.
всех вершин графа.
2. Выпишите петли, кратные ребра, концевые вершины и ребра, мосты и точки сочленения.
3. Укажите какие-нибудь маршрут, цепь и цикл в графе.
4. Запишите матрицу смежности.
5. Запишите матрицу инцидентности.
6. Определите расстояния между всеми вершинами графа и укажите максимальное удаление каждой вершины. Найдите центры, радиус, диаметр. Постройте какую-нибудь диаметральную цепь.
7. Найдите цикломатическое число графа и постройте дерево, покрывающее граф (остовное дерево графа).
8. Определите, является ли граф двудольным. Постройте максимальную двудольную часть графа.
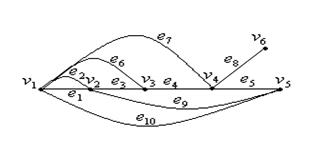
Задача 2.Постройте граф по матрице инцидентности и запишите матрицу смежности
а) 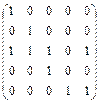 , б)
, б) 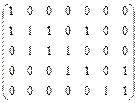 ,
,
в) 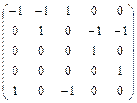 , г)
, г) 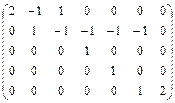 .
.
Задача 3.Постройте граф по матрице смежности и запишите матрицу инцидентности
а) 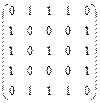 , б)
, б) 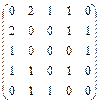 , в)
, в) 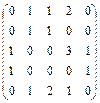 .
.
Дополнительные задачи по графам
1. Подряд в строчку записано 2012 цифр. Каждое двузначное число, записываемое двумя соседними цифрами (в том порядке, в каком они написаны) делится на 17 или на 23. а) Последняя цифра 1. Какова первая? б). Первая цифра 9. Какова последняя? Как изменится ответ, если цифр будет 2013?
2. Архипелаг состоит из 7 островов, расположенных вблизи материка. С каждого острова ведет 3 моста. Между любыми двумя островами, а также между каждым островом и материком имеется не более одного моста. С острова Чунга на остров Чанга переехать нельзя. Сколько мостов связывает острова архипелега с материком?
3. Серия предельных углеводородов имеет формулу 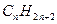 . Каждый атом углерода
. Каждый атом углерода 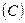 имеет всегда валентность 4, а каждый атом водорода
имеет всегда валентность 4, а каждый атом водорода 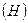 — валентность 1. Нарисуйте графы, представляющие: а) метан
— валентность 1. Нарисуйте графы, представляющие: а) метан 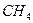 ; б) этан
; б) этан 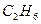 ; в) бутан
; в) бутан 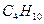 ; г) пентан
; г) пентан 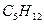 ; д) гексан
; д) гексан 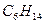 .
.
4. Город Зурбаган ограничен кольцевой дрогой. Все улицы начинаются и кончаются на этой дороге и никакие две улицы не имеют двух различных пересечений. Части, на которые улицы разбивают город, называются микрорайонами. В городе ввели одностороннее движение по улицам и кольцевой дороге. Докажите, что хотя бы один микрорайон можно объехать вокруг, не нарушив правил движения.
5. Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный», либо «синий» граф не является плоским.
6. На вечеринку пришли 7 супружеских пар. При встрече некоторые участники вечеринки обменялись рукопожатиями (естественно супруги руки друг другу не пожимают). После этого мистер Браун спросил у всех остальных участников о числе сделанных ими рукопожатий. Все названные числа оказались различными. Сколько рукопожатий сделала миссис Браун?
7. В одной стране каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение так, чтобы, выехав из любого города, в него нельзя было вернуться. Можно ли так сделать?
МАРШРУТЫ
Задача 1. Проверьте эйлеровость и гамильтоновость графа. Найдите маршрут минимальной длины, соединяющий вершины 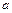 и
и 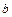 .
.
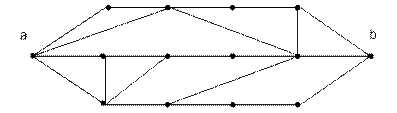
Задача 2. Проверьте эйлеровость и гамильтоновость графа. Найдите маршрут минимальной длины, соединяющий вершины 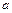 и
и 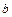 сведением к ненагруженному графу.
сведением к ненагруженному графу.
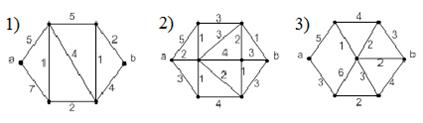
Задача 3. Проверьте эйлеровость и гамильтоновость графа. Используя алгоритм Дейкстры, найдите маршрут минимальной длины, соединяющий вершины 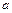 и
и 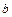 .
.
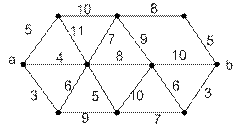
Задача 4. Проверьте эйлеровость графа. Используя алгоритм Дейкстры, найдите маршрут минимальной длины, соединяющий вершины 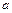 и
и 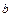 .
.
ЛЕС И ДЕРЕВЬЯ
Задача 1. а) Лист бумаги разрезается на 3 части. Некоторые из полученных листиков снова разрезаются на 3 части и т.д. Сколько получится листиков бумаги, если всего было разрезано 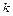 листов?
листов?
б) Имеется 3 листа бумаги. Некоторые из них разрезаются на 3 части, некоторые из полученных листиков снова разрезаются на 3 части и т.д. Сколько получится листиков бумаги, если всего было разрезано 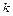 листов?
листов?
в) Сколько получится листиков бумаги, если первоначально имелось 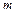 листков, некоторые из них разрезали на 5 частей и т.д., а всего было разрезано
листков, некоторые из них разрезали на 5 частей и т.д., а всего было разрезано 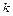 листов?
листов?
г) Сколько получится листиков бумаги, если первоначально имелось 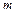 листков, некоторые из них разрезали на
листков, некоторые из них разрезали на 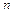 частей и т.д., а всего было разрезано
частей и т.д., а всего было разрезано 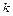 листов?
листов?
Задача 2. Имеется 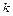 ящиков, в некоторых из них еще
ящиков, в некоторых из них еще 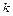 ящиков, в некоторых из последних еще
ящиков, в некоторых из последних еще 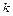 ящиков и т.д. Сколько всего ящиков, если заполненных
ящиков и т.д. Сколько всего ящиков, если заполненных 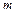 ?
?
Задача 3. У царя Гвидона было 5 детей. Из всех его потомков (детей, внуков, правнуков и т.д. 57 имели троих сыновей, а остальные умерли бездетными. Сколько потомков было у царя Гвидона?
Задача 4. Какое максимальное и минимальное количество висячих вершин может иметь дерево с 9 вершинами?
Задача 5. Изобразите все неизоморфные деревья с 6 вершинами.
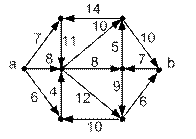
Задача 6. Дано дерево 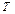 . 1) Постройте его в стандартной форме с корнем в вершине а) 11, б) 2. 2) Запишите упорядоченные
. 1) Постройте его в стандартной форме с корнем в вершине а) 11, б) 2. 2) Запишите упорядоченные
последовательности весов вершин в каждом случае.
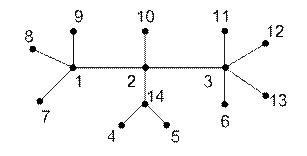
Задача 7. Постройте минимальное соединение графа и найдите его длину
9. АЛГЕБРА ВЫСКАЗЫВАНИЙ
1. Составьте таблицу истинности для высказываний 1. 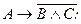 2
2 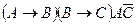 ; 3.
; 3. 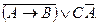 .
.
2. Проверьте, будут ли равносильными формулы
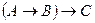 и
и 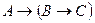 .
.
3. Проверьте, является ли заключение логическим следствием посылок
1). Если цены высоки, то и заработная плата высока.
Цены высоки или применяется регулирование цен.
Если применяется регулирование цен, то нет инфляции.
Наблюдается инфляция.
Следовательно, заработная плата высока.
2). Если завтра будет холодно, то я надену теплое пальто, если рукав будет починен.
Завтра будет холодно, а рукав не будет починен.
Следовательно, я не надену теплое пальто.
3). 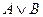 ,
, 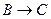 ,
, 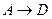 . Следовательно,
. Следовательно, 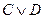 .
.
4. Существует предание, что Александрийскую библиотеку сжег калиф Омар. Свое деяние он оправдал с помощью следующего рассуждения: «Если ваши книги согласны с Кораном, то они излишни. Если они не согласны с Кораном, то они вредны. Но вредные или излишние книги следует уничтожить. Значит, ваши книги следует уничтожить».
