Вынужденные колебания в последовательном колебательном контуре
Краткая теория.
Свободные колебания в последовательном колебательном контуре.
Последовательный колебательный контур (рис. 1) содержит конденсатор емкостью C и катушку индуктивностью L и сопротивлением R. Пусть в момент времени t = 0 на конденсаторе имеется заряд 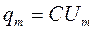 . При разрядке конденсатора через катушку возникнет ток и на основе второго закона Кирхгофа
. При разрядке конденсатора через катушку возникнет ток и на основе второго закона Кирхгофа
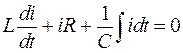 | (1) |
Учитывая, что 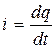 уравнение (1) может быть преобразовано к виду
уравнение (1) может быть преобразовано к виду
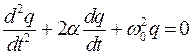 , , | (2) |
где
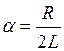 , , 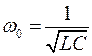 , , | (3) |
(a - коэффициент затухания, w0 – собственная частота контура).
Если 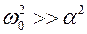 , решение уравнения (2)может быть записано в виде:
, решение уравнения (2)может быть записано в виде:
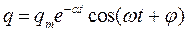 , , | (4) |
где 
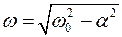 .
.
Таким образом, при 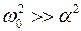 зависимость заряда на конденсаторе от времени имеет характер затухающих колебаний, частота которых w, называемая частотой свободных колебаний, несколько меньше собственной частоты контура w0. Постоянные qm и j зависят от начальных условий. В рассматриваемом случае можно считать w»w0 и j»0; тогда (4) принимает вид:
зависимость заряда на конденсаторе от времени имеет характер затухающих колебаний, частота которых w, называемая частотой свободных колебаний, несколько меньше собственной частоты контура w0. Постоянные qm и j зависят от начальных условий. В рассматриваемом случае можно считать w»w0 и j»0; тогда (4) принимает вид:
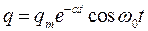 . . | (5) |
Закон изменения силы тока можно найти, дифференцируя (5) по времени с учетом, что 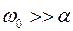 . Тогда
. Тогда
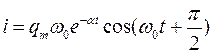 . . | (6) |
Уравнение (6) дает следующее соотношение между амплитудами тока и напряжения:
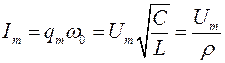 ,
,
где
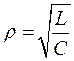 | (7) |
волновое или характеристическое сопротивлением контура и является одной из его основных характеристик, так как активное сопротивление контура не влияет на соотношение между Um и Im; оно определяет лишь степень затухания колебаний, т.е. быстроту уменьшения амплитуд с течением времени.
Кроме коэффициента затухания a для характеристики затухающих колебаний пользуются логарифмическим декрементом затухания, который равен натуральному логарифму отношения амплитуд колебаний, взятых через период Т:
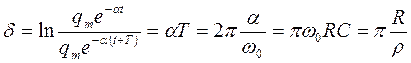 . . | (8) |
Важным параметром колебательного контура является добротность Q, характеризующая относительную убыль энергии в процессе колебаний:
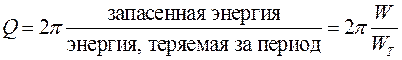 . . | (9) |
Энергия теряемая в контуре за один период, согласно закону Джоуля – Ленца, равна 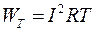 , где I – эффективное значение переменного тока. Энергия, запасенная колебательной системой, равна максимальной энергии, накопленной конденсатором или катушкой индуктивности:
, где I – эффективное значение переменного тока. Энергия, запасенная колебательной системой, равна максимальной энергии, накопленной конденсатором или катушкой индуктивности: 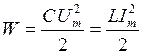 . Подставляя в (9) выражения для W и WТ, получим:
. Подставляя в (9) выражения для W и WТ, получим:
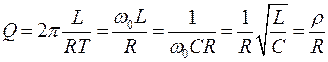 . . | (10) |
Вынужденные колебания в последовательном колебательном контуре.
Пусть контур подключен к источнику внешней гармонической ЭДС с амплитудой Еm:
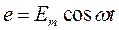 .
.
В соответствии с законом Кирхгофа получаем:
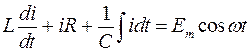 , , | (11) |
Решение уравнения (9) можно получить в виде:
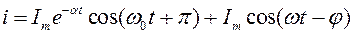 . . | (12) |
Таким образом, при воздействии на контур периодической ЭДС колебательный процесс в нем вначале представляет собой суперпозицию свободных и вынужденных колебаний. Так как свободные колебания имеют затухающий характер, по истечении некоторого времени ими можно пренебречь и считать, что в контуре существуют лишь вынужденные колебания. Чем выше добротность контура, тем медленнее затухают свободные колебания.
Резонансом в последовательном контуре называется такое явление, при котором резко возрастает амплитуда вынужденных колебаний силы тока, реактивная составляющая входного сопротивления контура равна нулю и контур представляет для генератора чисто активную нагрузку. Резонанс в последовательном колебательном контуре называют резонансом напряжений.
Из этого вытекают следующие свойства резонанса в последовательном контуре:
1. При резонансе реактивное сопротивление 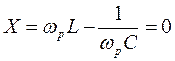 , поэтому частота генератора
, поэтому частота генератора
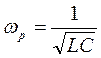 ; ; | (13) |
но 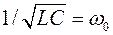 , т.е. резонанс в последовательном контуре происходит при частоте генератора wр равной собственной частоте контура w0. Строго говоря, это не всегда правильно, так как при наличии в контуре сопротивления R собственная частота его w0 отличается, хотя и весьма незначительно, от
, т.е. резонанс в последовательном контуре происходит при частоте генератора wр равной собственной частоте контура w0. Строго говоря, это не всегда правильно, так как при наличии в контуре сопротивления R собственная частота его w0 отличается, хотя и весьма незначительно, от 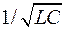 .
.
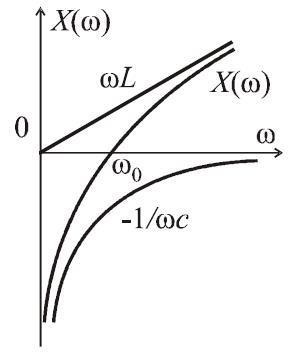
Рис. 2
Характер изменения реактивных сопротивлений катушки индуктивности XL, емкости ХС и контура в целом Х от частоты показан на рис. 2. Следует иметь в виду, что на частотах ниже резонансной сопротивление контура носит емкостной характер, а на частотах выше резонансной – индуктивный.
2. Равенство 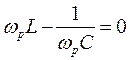 , при условии. что wр = w0=
, при условии. что wр = w0= 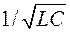 , дает
, дает
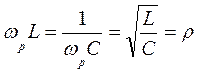 . . | (14) |
Таким образом, при резонансе индуктивное и емкостное сопротивления контура порознь равны его характеристическому сопротивлению.
Так как при резонансе Х = 0, то полное сопротивление контура:
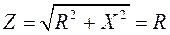
Отсюда следует, что между амплитудными значениями ЭДС Еm и тока Imp существует зависимость:
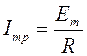 . . | (15) |
3. При резонансе ток и ЭДС генератора совпадают по фазе.
4. По формулам (14) и (15) устанавливаем соотношения между резонансными амплитудами напряжений на индуктивности 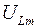 , емкости
, емкости 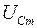 и ЭДС генератора
и ЭДС генератора 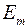 :
:
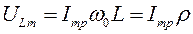 ,
, 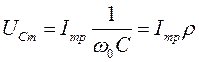 ,
, 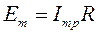 ,
,
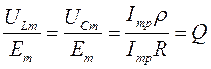 | (16) |
Из выражения (16) следует, что при резонансе в последовательном контуре амплитуды напряжения на индуктивности и емкости равны между собой и каждая из них превышает амплитуду ЭДС генератора в Q раз. Вследствие наличия активного сопротивления в контуре максимум значений 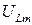 ,
, 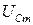 и
и 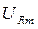 достигается при несколько различных значениях частот. И чем выше добротность контура, тем ближе эти значения.
достигается при несколько различных значениях частот. И чем выше добротность контура, тем ближе эти значения.
Определим зависимость тока в контуре от частоты в относительном масштабе:
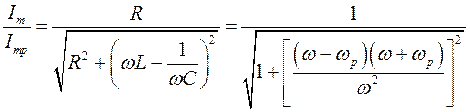 . . | (17) |
В случае использования контура в качестве фильтрующего элемента имеет смысл анализировать поведение тока в нем при относительно небольших отклонениях частоты сигнала от резонансной. С учетом этого можно принять, что 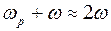 . Если отклонение частоты от резонансной (расстройку) обозначить через
. Если отклонение частоты от резонансной (расстройку) обозначить через 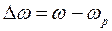 то (17) примет вид
то (17) примет вид
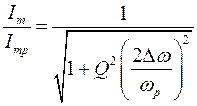 . . | (18) |
Это соотношение является аналитическим описанием резонансной, или амплитудно-частотной, характеристики контура. Из него видно, что значительные токи в контуре возникают лишь при небольших 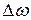 , а следовательно, контур обладает фильтрующими (избирательными) свойствами. Избирательные свойства контура, т.е. способность ослаблять сигналы, частота которых отличается от резонансной, характеризуются полосой пропускания.
, а следовательно, контур обладает фильтрующими (избирательными) свойствами. Избирательные свойства контура, т.е. способность ослаблять сигналы, частота которых отличается от резонансной, характеризуются полосой пропускания.
Полосой пропускания контура ΔF или ΔΩ (ΔΩ = 2π ΔF) называется область частот вблизи резонансной, на границах которой отношение токов (или напряжений) 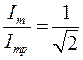 .
.
Из соотношения (18) можно получить связь между полосой пропускания, резонансной частотой и добротностью:
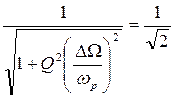 ,
,
откуда легко найти, что
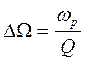 или или 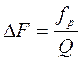 . . | (19) |
Ряд нормированных амплитудно-частотных характеристик контуров, отличающихся только добротностью Q, показан на рис. 3.
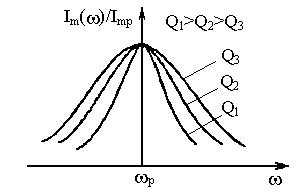 Рис. 3
Рис. 3
Фазочастотной характеристикой (ФЧХ) называют зависимость фазового сдвига j тока в контуре относительно вызывающей его ЭДС от частоты. Для последовательного контура имеем
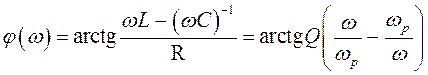 .
.
Выполнение работы.
Работа выполняется с использованием стенда, схема которого изображена на рис 4. Источником внешней ЭДС является генератор звуковой частоты. В контур последовательно включены резистор R переменного сопротивления, катушка индуктивности и конденсатор переменной емкости. Активное сопротивление контураопределяется суммой сопротивления катушки (ее активного сопротивления, измеренного на постоянном токе), резистора и выходного сопротивления генератора. Эффективное значение напряжения на конденсаторе измеряется вольтметром V.
Подключить вольтметр к конденсатору. Емкость конденсатора, сопротивление резистора, выходное напряжение генератора укажет преподаватель. Изменяя частоту f в диапазоне (2…20) кГц, измерить зависимость напряжения на конденсаторе UC от частоты для двух значений сопротивления.
Подключить вольтметр к катушке индуктивности и измерить зависимость напряжения UL от частоты для двух значений сопротивления.
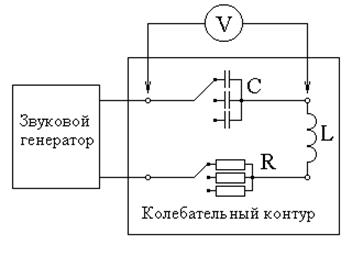 Рис. 4.
Рис. 4.
Задание
1. Для двух сопротивлений контура рассчитайте Q, a, r, ΔF, ΔΩ, wр и fр (fр=wр/2p). Полное активное сопротивление контура равно сумме активного сопротивления катушки, выходного сопротивления генератора и сопротивления резистора. Значения выходного сопротивления генератора и сопротивления резистора, а также емкость конденсатора укажет преподаватель.
2. Снимите зависимости напряжения на конденсаторе UС от частоты f для двух значений сопротивления вблизи резонансной частоты fр. Полученные данные занесите в таблицы 1 и 2.
Таблица 1 и 2 (нарисовать две таблицы)
| R= C= L= | ||||||||||||||||||||
| f, кГц | ||||||||||||||||||||
| UC, В |
3. Снимите зависимости напряжения на катушке UL от частоты f для двух значений сопротивления вблизи резонансной частоты fр. Полученные данные занесите в таблицы 3 и 4.
Таблица 3 и 4 (нарисовать две таблицы)
| R= C= L= | ||||||||||||||||||||
| f, кГц | ||||||||||||||||||||
| UC, В |
4. По данным таблиц постройте резонансные кривые (см. рис. 5) 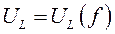 ,
, 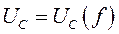 .
.
5. Из графиков определите экспериментальную резонансную частоту fрэксп и полосу пропускания контура ΔFэксп. Полученные результаты сравнить с рассчитанными значениями.
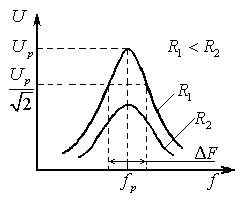 Рис. 5.
Рис. 5.
