Сила Лоренца. Движение заряженных частиц в магнитном поле

При движении заряженных частиц в магнитном поле на них действует сила, называемая силой Лоренца 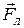, направленная перпендикулярно скорости частицы 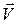и индукции магнитного поля :

,

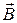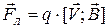где q- заряд частицы.

Величину силы Лоренца можно вычислить по формуле модуля векторного произведения:

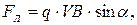
где a - угол между направлением скорости и индукции магнитного поля. На рис.7.1 показано расположение указанных векторов в случае положительного заряда.

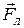
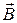
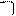a

Рис.7.1

Поскольку движение заряженной частицы в магнитном поле эквивалентно току, ясно что направление силы Лоренца можно определять как и силы Ампера, по правилу левой руки. Следует при этом иметь в виду, что за направление тока принимается движение положительного заряда. Закон Ампера может быть получен из выражения для силы Лоренца, если просуммировать все силы, действующие на движущиеся в проводнике носители заряда при протекании по нему тока, поэтому можно сказать, что проявление силы Лоренца является более фундаментальным научным фактом.

Наличие силы, действующей на заряженные частицы в магнитном поле, существенно определяет характер их движения. Очень важным является то, что сила перпендикулярна скорости. Как известно из механики, такая сила не совершает работы, следовательно, сохраняется кинетическая энергия, а следовательно и модуль скорости частицы. Рассмотрим три возможных случая:

1. Если частица движется вдоль силовых линий магнитного поля ( 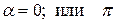), то сила Лоренца обращается в нуль и частица движется равномерно и прямолинейно.

2. Если частица влетает в магнитное поле перпендикулярно силовым линиям ( 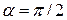), то она движется с ускорением 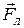/m, перпендикулярным скорости и магнитному полю, с постоянной по величине скоростью. Такое движение представляет собой равномерное вращение по окружности вокруг силовой линии магнитного поля. Получим выражение для радиуса окружности. Если скорость равна 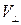, то сила Лоренца имеет величину 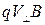, и II закон Ньютона для движения по окружности дает выражение: 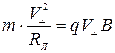, из которого и получим выражение для радиуса и периода вращения T:

; .

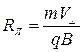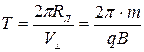Важно, что период вращения не зависит от скорости частицы, поэтому частицы одного сорта делают один оборот вокруг силовой линии за одинаковое время, хотя радиус окружности зависит от скорости частиц.

3. В общем случае, частица, влетающая в магнитное поле со скоростью V, имеет составляющую скорости вдоль магнитного поля, равную 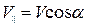и перпендикулярную полю 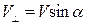. Таким образом, результирующее движение представляет совокупность равномерного вращения вокруг силовой линии и дрейф вдоль силовой линии с постоянной скоростью. Траектория такого движения представляет винтовую линию. Радиус винтовой линии и период вращения определяются прежде полученными соотношениями. Расстояние между витками или шаг винтовой линии h может быть вычислен по формуле:

.

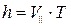Движение заряженных частиц в магнитных полях встречается во многих природных явлениях, таких как полярные сияния, солнечные вспышки. В частности, жизнь на Земле обязана своим существованием наличию силы Лоренца. Заставляя космические заряженные частицы двигаться по окружности, земное магнитное поле защищает поверхность планеты от высокоэнергичных корпускул. Энергичные частицы совершают движение по винтовым линиям вдоль магнитного поля, образуя радиационные пояса Земли.

Особенности движение заряженных частиц в магнитном поле используются в физике высоких энергий (ускорители), в электронике для создания генераторов излучения, в термоядерной энергетике для магнитного удержания плазмы.