Тригонометрические неравенства
Для решения тригонометрических неравенств используют единичную окружность и определение тригонометрических функций или графический метод. Используют также метод замены переменной.
1. Простейшие тригонометрические неравенства
И неравенства, сводящиеся к ним
Пример 1.Решить неравенство
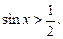
Решение. Воспользуемся определением синуса. С помощью единичной окружности находим вначале углы 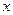 , которые соответствуют равенству
, которые соответствуют равенству 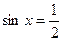 . Их два:
. Их два: 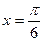 и
и 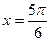 (рис. 25). Строим их, причем соответствующие радиус-векторы пунктиром, т.к. заданное неравенство строгое.
(рис. 25). Строим их, причем соответствующие радиус-векторы пунктиром, т.к. заданное неравенство строгое.
Выделим на единичной окружности множество точек, ординаты которых больше 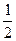 , это
, это 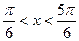 . Используя периодичность функции
. Используя периодичность функции 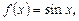 приходим к ответу:
приходим к ответу:
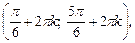
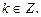
 |
Рис. 25
Ответ неравенства следует понимать как объединение всех промежутков, которые получаем при всех 
Пример 2. Решить неравенство
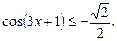
Решение.Заменив 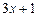 на t, получим:
на t, получим: 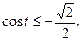 Выделим на единичной окружности множество точек, абсциссы которых меньше или равны
Выделим на единичной окружности множество точек, абсциссы которых меньше или равны 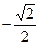 (рис.26). Получим:
(рис.26). Получим:
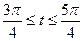 ,
,
учитывая период
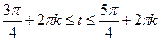 .
.
Возвращаемся к заданной неизвестной:
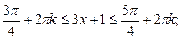
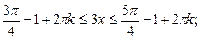
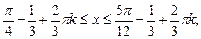
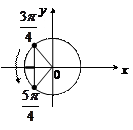
Рис. 26
Приходим к ответу:
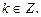
Пример 3. Решить неравенство
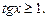
Решение. Используем графический метод. Построим график функции 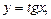 при этом ограничимся промежутком длиной в период
при этом ограничимся промежутком длиной в период 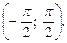 Проведем прямую
Проведем прямую 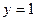 (рис. 17). Найдем промежуток оси абсцисс на которой график проходит не ниже построенной прямой. Этот промежуток и будет решением неравенства на рассматриваемом интервале, т.е.
(рис. 17). Найдем промежуток оси абсцисс на которой график проходит не ниже построенной прямой. Этот промежуток и будет решением неравенства на рассматриваемом интервале, т.е. 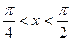 . С учетом периодичности функции
. С учетом периодичности функции 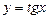 получим
получим
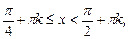
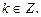
 |
Рис. 27
Приходим к ответу:
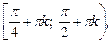
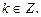
Пример 4. Решить неравенство
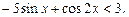
Решение. 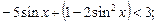
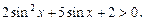
Заменим 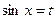 . Имеем:
. Имеем:
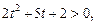
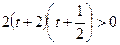 ,
,
т.е. получаем
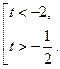
Возвращаемся к старой переменной:
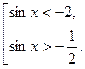
Первое неравенство совокупности решения не имеет. Решаем второе. С помощью единичной окружности получаем:
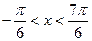 .
.
Учитываем период и приходим к ответу:
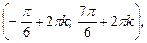
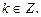
Задания для самостоятельного решения
I уровень
1.1. Решите неравенство:
1) 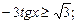 2)
2) 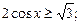
3) 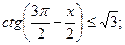 4)
4) 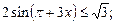
5) 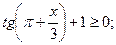 6)
6) 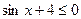 .
.
II уровень
2.1. Решите неравенство:
1) 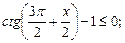 2)
2) 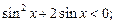
3) 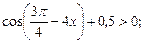 4)
4) 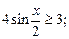
5) 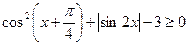 ;
;
6) 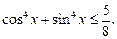
III уровень
3.1. Решите неравенство:
1) 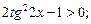 2)
2) 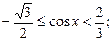
3) 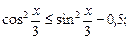 4)
4) 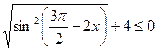 ;
;
5) 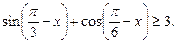 6)
6) 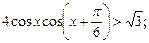
Тригонометрическая и показательная формы
Комплексного числа
Комплексное число 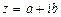 в прямоугольной декартовой системе координат
в прямоугольной декартовой системе координат 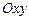 изображается точкой
изображается точкой 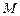 .
.
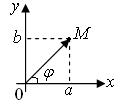 |
Рис. 28
Длина радиус-вектора точки  (рис.28) называется модулем комплексного числа
(рис.28) называется модулем комплексного числа  и обозначается
и обозначается  или
или 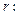
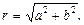 (29)
(29)
Угол 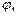 образованный этим вектором с положительным направлением действительной оси
образованный этим вектором с положительным направлением действительной оси 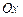 называется аргументом числа
называется аргументом числа 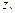 Связь между аргументом
Связь между аргументом 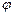 комплексного числа и его действительной и мнимой частью выражается формулами:
комплексного числа и его действительной и мнимой частью выражается формулами:
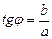 (30)
(30)
или
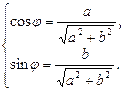 (31)
(31)
Аргумент комплексного числа определен неоднозначно: если 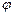 – аргумент числа
– аргумент числа 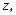 то
то 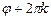 – также аргумент этого числа при любом целом
– также аргумент этого числа при любом целом 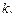 Для однозначности определения аргумента его выбирают в пределах
Для однозначности определения аргумента его выбирают в пределах 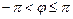 (или
(или 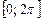 ), такое значение аргумента называют главным и обозначают
), такое значение аргумента называют главным и обозначают 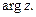 Всюду далее будем рассматривать главное значение аргумента:
Всюду далее будем рассматривать главное значение аргумента: 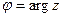 .
.
На практике находить аргумент комплексного числа 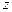 имеет смысл согласно формуле (30) с учетом координатной четверти, в которой лежит число
имеет смысл согласно формуле (30) с учетом координатной четверти, в которой лежит число 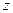 или формул (31).
или формул (31).
Запись комплексного числа в виде
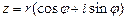 (32)
(32)
называется тригонометрической формой комплексного числа.
Пусть 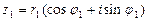 и
и 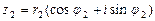 комплексные числа, заданные в тригонометрической форме. Тогда для произведения
комплексные числа, заданные в тригонометрической форме. Тогда для произведения 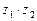 и частного
и частного 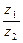 справедливы формулы:
справедливы формулы:
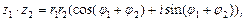 (33)
(33)
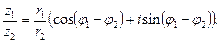 (34)
(34)
Для комплексного числа 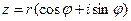 справедлива формула Муавра:
справедлива формула Муавра:
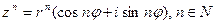 (35)
(35)
Корнем 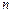 -й степени из комплексного числа
-й степени из комплексного числа 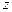 называется комплексное число
называется комплексное число 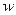 такое, что
такое, что 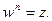
Корень 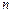 -й степени из комплексного числа
-й степени из комплексного числа 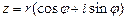 имеет
имеет 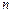 различных значений, которые находят по формуле
различных значений, которые находят по формуле
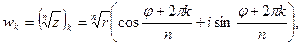 (36)
(36)
где 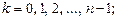
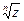 – арифметическое значение корня.
– арифметическое значение корня.
Все значения корня 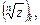
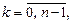 расположены на окружности с центром в начале системы координат и радиусом
расположены на окружности с центром в начале системы координат и радиусом 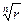 в вершинах правильного вписанного в окружность
в вершинах правильного вписанного в окружность 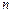 -угольника.
-угольника.
Соотношение
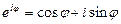 (37)
(37)
называется формулой Эйлера.
Пусть комплексное число 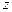 записано в тригонометрической форме Используя формулу Эйлера (37) можно записать:
записано в тригонометрической форме Используя формулу Эйлера (37) можно записать:
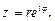 (38)
(38)
Такая форма записи называется показательной формой комплексного числа.
Правила действий над комплексными числами в показательной форме:
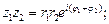 (39)
(39)
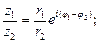 (40)
(40)
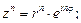 (41)
(41)
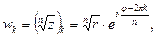 где
где 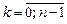 (42)
(42)
Пример 1. Представить в тригонометрической форме комплексное число:
1) 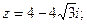 2)
2) 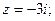 3)
3) 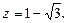
Решение. 1.Находим модуль данного числа по формуле (29):
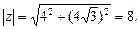
Для нахождения аргумента  используем формулу (30):
используем формулу (30):
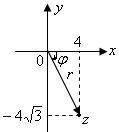
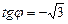 и число
и число 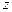 лежит в четвертой четверти. Поэтому
лежит в четвертой четверти. Поэтому 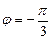 (рис. 29).
(рис. 29).
Рис. 19
Рис.29
Подставим полученные значения 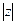 и
и 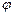 в формулу (32), получим
в формулу (32), получим
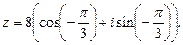
2. В данном случае 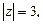
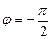 (точка, изображающая данное число принадлежит отрицательной части мнимой оси (рис. 30).
(точка, изображающая данное число принадлежит отрицательной части мнимой оси (рис. 30).
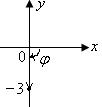
Рис. 30
Поэтому 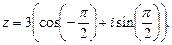
3. Находим модуль комплексного числа 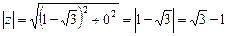 (так как
(так как 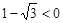 ),
), 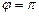 (заданное число является отрицательным действительным числом (рис. 31)).
(заданное число является отрицательным действительным числом (рис. 31)).
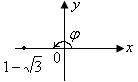
Рис. 31
Поэтому 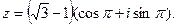
Пример 2. Выполнить действия:
1) 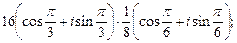
2) 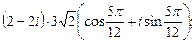
3) 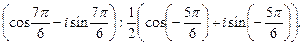
Решение. 1. Используя формулу (33), находим:
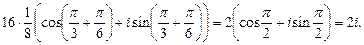
2. Сначала представим число 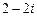 в тригонометрической форме. Имеем
в тригонометрической форме. Имеем 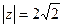 . Поскольку число лежит в IV четверти и
. Поскольку число лежит в IV четверти и 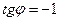 , то
, то 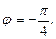 Значит,
Значит,
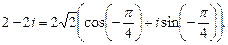
Теперь воспользуемся формулой (33):
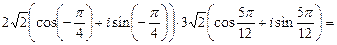
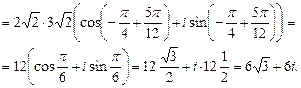
Получили ответ: 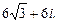
3. Заметим, что делимое число не записано в тригонометрической форме. Запишем его в этой форме. Получим:
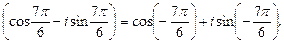
Используя формулу (34) находим:
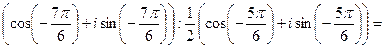
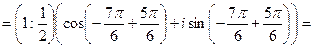
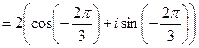 .
.
Переходя к алгебраической форме, получаем в ответе 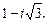
Пример 3. Возвести в степень 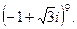
Решение. Представим число 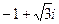 в тригонометрической форме. Здесь
в тригонометрической форме. Здесь 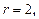
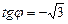 и соответствующая точка лежит во второй четверти, т. е.
и соответствующая точка лежит во второй четверти, т. е. 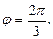
Получили 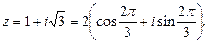 По формуле (35) находим:
По формуле (35) находим:
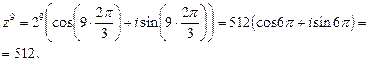
Ответ: 512.
Пример 4. Извлечь корень. Полученные значения корня изобразить на комплексной плоскости:
1) 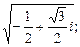 2)
2) 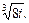
Решение. 1. Находим модуль и аргумент числа 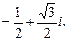
Получаем 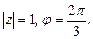 Далее, используя формулу (36), вычисляем
Далее, используя формулу (36), вычисляем
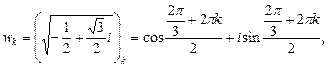
где 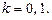
Если 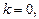 то
то 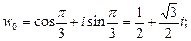
если 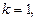 то
то 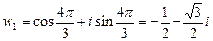 (рис. 32).
(рис. 32).
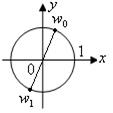 |
Рис. 32
2. Находим модуль и аргумент числа 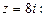
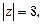
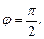 Получили
Получили 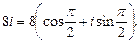 Тогда, используя формулу (36), получаем
Тогда, используя формулу (36), получаем
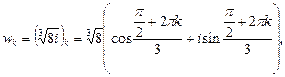
где 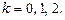
Если 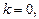 то
то
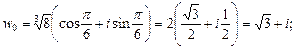
если 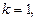 то
то
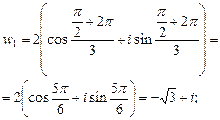
если 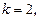 то
то
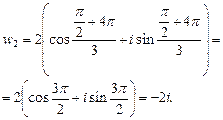
Изобразим комплексные числа  . На комплексной плоскости точки, соответствующие значениям корня, являются вершинами правильного треугольника, вписанного в окружность радиусом
. На комплексной плоскости точки, соответствующие значениям корня, являются вершинами правильного треугольника, вписанного в окружность радиусом  с центром в начале координат (рис. 33).
с центром в начале координат (рис. 33).
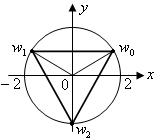 |
Рис. 33
Пример 5. Представить число в показательной форме:
1) 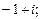 2)
2) 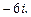
Решение. 1. Находим модуль и аргумент комплексного числа 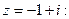
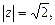
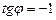 и число лежит во 2-й четверти, значит
и число лежит во 2-й четверти, значит 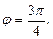 Получили
Получили 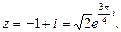
2. Находим модуль и аргумент комплексного числа 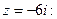
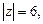
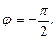 Тогда, по формуле (38) имеем:
Тогда, по формуле (38) имеем:
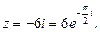
Пример 6.Решить уравнение 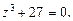
Решение. 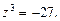 Искомыми корнями уравнения будут значения
Искомыми корнями уравнения будут значения 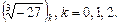
Для 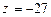 имеем
имеем 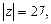
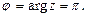 Тогда
Тогда 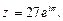 По формуле (42) получаем
По формуле (42) получаем
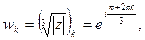
где k = 0, 1, 2.
Если k = 0, 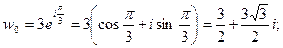
если k = 1, 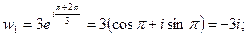
если k = 2, 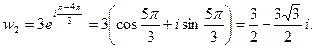
Таким образом, корнями заданного уравнения являются числа
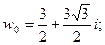
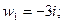
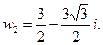
Пример 7. Изобразить на комплексной плоскости множество точек, для которых:
1) 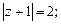 2)
2) 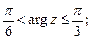 3)
3) 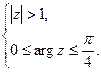
Решение. 1. Пусть 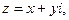 тогда
тогда
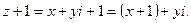
Найдем модуль полученного комплексного числа
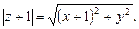
Тогда заданное равенство будет иметь вид
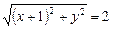 или
или 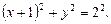
 Это уравнение окружности радиуса 2 с центром в точке
Это уравнение окружности радиуса 2 с центром в точке 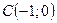 (рис. 34).
(рис. 34).
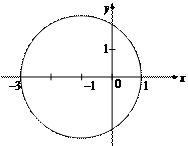 |
Рис. 34
2. Пусть 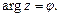 Из условия имеем
Из условия имеем 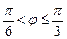 . Геометрически это неравенство задает на плоскости множество точек, лежащих внутри угла с вершиной в точке (0; 0), стороны которого составляют с положительным направлением оси Ох углы
. Геометрически это неравенство задает на плоскости множество точек, лежащих внутри угла с вершиной в точке (0; 0), стороны которого составляют с положительным направлением оси Ох углы 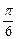 и
и 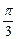 , а также множество точек, лежащих на луче
, а также множество точек, лежащих на луче 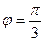 (рис. 35).
(рис. 35).

Рис. 35
3. Заданная система равносильна следующей:
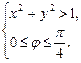
Решением системы будет пересечение множества точек, лежащих вне окружности 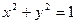 и множества точек, лежащих внутри угла величины
и множества точек, лежащих внутри угла величины 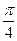 и на его сторонах (рис. 36).
и на его сторонах (рис. 36).
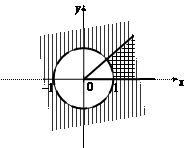 |
Рис. 36
