Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний

Изотермы, построенные при одной и той же температуре для разных газов, выглядят по-разному, потому что 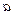и и 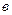связанные с ними критические величины 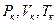различные для разных газов. Можно, однако, и для неидеальных газов написать уравнение изотермы, чтобы оно не зависело от природы газа, т.е. было бы универсальным. Для этого оказывается достаточно, чтобы параметры состояния газа находились в одинаковых отношениях к соответствующим критическим параметрам. Для этого введем безразмерные параметры, обезразмеренные с помощью критических величин, т.е.

.

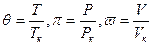Параметры 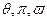называют приведенными параметрами. Поставим в уравнение Ван-дер-Ваальса значения параметров 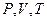, вырожденные через приведенные параметры. Получим:

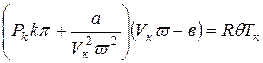. (5.12)

В (5.12) подставим значения 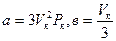. Тогда получим:

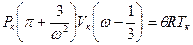. (5.13)

С учетом известных соотношений

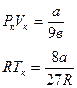
имеем:

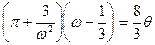. (5.14)

Уравнение (5.14) является приведенным уравнением состояния. В этом уравнении не содержатся константы, характерные для конкретного вещества. Из него следует, что если вещества обладают двумя одинаковыми приведенными параметрами из трех, то и третий параметр тоже одинаков для этих веществ. Этот закон носит название закона соответственных состояний. Он выражает тот факт, что изменяя масштаб, которым измеряются две из трех величин, характеризующих состояние веществ, т.е. используя приведенные параметры, можно совместить изотермы всех веществ.

Сжижение газов

Как следует из анализа изотерм Ван-дер-Ваальса, всякий газ может быть переведен в жидкое состояние путем сжатия, если его температура ниже критической температуры. Например, углекислый газ можно превратить в жидкость при комнатной температуре, поскольку его критическая температура равна 31,1⁰С. Но есть такие газы, которые при комнатной температуре нельзя перевести в жидкое состояние как бы его не сжали. К таким газам относятся, например, воздух, водород, гелий, кислород, у которых критические температуры значительно ниже комнатной. До открытия критической температуры (1822г.) их считали непослушными газами, т.е. газами, не способными сжижаться.

Для сжижения таких газов их необходимо охладить до температуры несколько ниже критической, после чего повышением давления газ может быть переведен в жидкое состояние. Сжиженный таким образом газы удобно хранить под атмосферным давлением (в открытом сосуде), но в этом случае их температура должна быть еще более низкой, чтобы давление соответствующее насыщенному пару, т.е. горизонтальному участку изотермы, было равно 1 атм. Для азота такая изотерма соответствует температуре -195,8⁰С, в то время как критическая температура азота равна -147,1⁰С.

Таким образом, чтобы газ сжижать, необходимо его достаточно сильно охладить. Для достижения такого сильного охлаждения используются два метода. Первый из них связан с использованием так называемого эффекта Джоуля-Томсона.

Эффект Джоуля-Томсона

Для наблюдения этого эффекта газ при достаточно большом давлении вынуждают протекать через пористую теплоизолированную перегородку. Это означает, что проток происходит адиабатно.

Гидродинамическое сопротивление перегородки приводит к тому, что на ней теряется, часть давления и газ выходит из перегородка при более низком давлении. Это означает, что газ расширяется или же дросселируется. Для того, чтобы течение газа было стационарным, т.е. происходило при постоянных значениях давлений, по обе стороны перегородки необходим какой-либо насос (компрессор), который поддерживал бы постоянным эти давления. Этот насос производит внешнюю работу сжатия газа, которая расходуется на преодоление сопротивления дросселя.

Покажем, что для неидеального газа процесс Джоуля-Томсона сопровождается изменением температуры, причем, такое же расширение идеального газа не вызывает никакого изменения температуры.

Явление изменения температуры газа при его адиабатном расширении дросселированием от одного постоянного давления к другому называется эффектом Джоуля-Томсона. Изменение температуры неидеального газа в процессе Джоуля-Томсона объясняется тем, что при расширении газа увеличивается расстояние между молекулами и совершается внутренняя работа против сил взаимодействия между молекулами. За счет этой работы изменяется кинетическая энергия молекул, а, следовательно, и температура.

Количественно эффект Джоуля-Томсона характеризуется дифференциальным коэффициентом Джоуля-Томсона 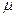, который определяется отношением изменения температуры газа 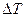к вызвавшему его изменению давления :

.

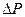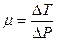Для вычисления этого коэффициента детально проанализируем этот процесс с помощью следующей схемы.

Пусть 1 моль газа занимает объем 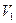между перегородкой и поршнем 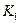(рис.7), а после прохождения через перегородку - объем 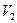между перегородкой и поршнем 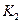. Поскольку при сжатии газа давление 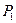остается постоянным внешняя работа 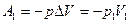. Газ, переходя через перегородку, расширяется и совершает работу 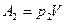. Общая работа расширения газа

.

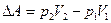Так как процесс Джоуля-Томсона является адиабатическим 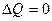. Согласно первому закону термодинамики, работа 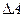должна равняться изменению внутренней энергии, т.е.

,

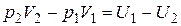где 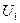и 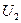- внутренняя энергия моля газа до и после расширения. Это выражение можно переписать следующим образом:

.

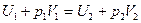Термодинамический потенциал 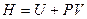мы назвали энтальпией. Таким образом, процесс Джоуля-Томсона происходит так, что энтальпия остается постоянной по обе стороны перегородки, т.е.

.

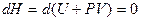Для идеального газа 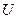и 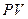зависят только от температуры, поэтому и энтальпия 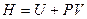зависит только от температуры. Равенство энтальпий по обе стороны перегородки означает и равенство температур. Значит, для идеального газа коэффициент Джоуля-Томсона равен нулю. Для неидеального газа внутренняя энергия зависит не только от температуры, но и от объема 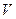, занимаемого газом. Кроме того, 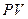зависит от объема. Поэтому в случае неидеального газа равенство энтальпий по стороне перегородки не означает равенство температур.

Действительно, опыт показывает, что большинство газов, такие как азот, кислород, углекислота в процессе дросселирования при комнатной температуре охлаждаются. Но такие газы как водород, гелий при тех же условиях нагреваются.

Отметим, что процесс Джоуля-Томсона необратимый, следовательно, он сопровождается увеличением энтропии .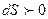

Выражение для дифференциала энтальпии, как было показано выше, имеет вид

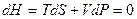. (5.15)

Воспользуемся выражением (1.51) для дифференциала энтропии 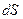через изменение температуры 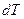и изменение давления :

.

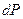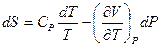Поставляя это выражение в (5.15) получим:

.

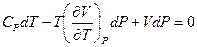Отсюда получим выражение для коэффициента Джоуля-Томсона:

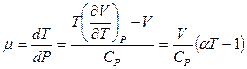, (5.16)

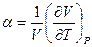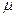где - коэффициент объемного расширения газа. Все величины, входящие в выражение для могут быть определены, если известно уравнение состояния газа.

Из формулы (5.16) следует, что знак коэффициента 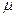зависит от величины .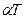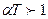

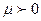При , при 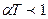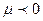. Для идеального газа 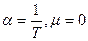. Для реальных газов 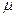может быть как положительным, так и отрицательным. Более того, для одного и того же газа в одной области температур 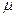может быть положительным, а в другой - отрицательным. Существует температура 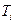, характерная для данного газа, при которой коэффициент Джоуля-Томсона меняет свой знак. Эта температура называется температурой инверсии.

Вычислим коэффициент Джоуля-Томсона для газа Ван-дер-Ваальса. Для этого необходимо вычислить производную 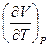. Для этого раскроем скобки в левой части уравнения Ван-дер-Ваальса (5.5) и получим

.

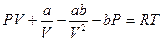Продифференцируем обе части уравнения по 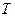при :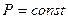

.

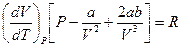Вместо 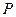поставим его значение из уравнения Ван-дер-Ваальса (5.5)и получим

.

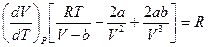Приведя выражение в квадратных скобках к общему знаменателю, получим:

.

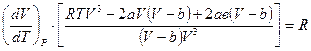После преобразования квадратной скобки, имеем:

.

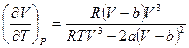Поставив это выражение в (5.16), получим:

.

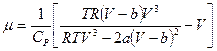После приведения квадратной скобки к общему знаменателю, имеем следующее выражение для коэффициента Джоуля-Томсона:

,

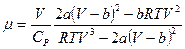которое можно переписать в виде:

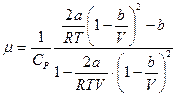. (5.17)

Если давление газа не очень велико (порядка 100-200 атм.), то 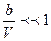, 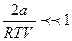и ими в (5.17) можно пренебречь. Тогда

.

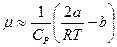Из этой формулы видно, что коэффициент Джоуля-Томсона положителен, ес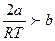ли ил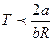и . При 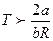коэффициент Томсона 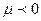, т.е. газ при дросселировании нагревается. Температура инверсии 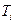определяется равенством .

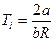Тот факт, что в опыте Джоуля-Томсона, который ставился при комнатной температуре, водород при расширении нагревался, в то время как другие газы охлаждались, не является, конечно, особым свойством водорода. Любой газ обнаружит такие же свойства, если ставить опыт при температуре более высокой, чем температура инверсии.

Вопросы для самоконтроля изученного материала

Реальные газы

1. В чем отличие реального газа от идеального? При каких условиях в поведении газов наступает отступление от законов Менделеева-Клапейрона?

2. Каков физический смысл поправок в уравнении Ван-дер-Ваальса? Как они вычисляются: а) из молекулярно-кинетической теории; б) через параметры критического состояния?

3. Как будут располагаться изотермы Ван-дер-Ваальса на графике PV для различных температур? Какой вид будет иметь изотерма Ван-дер-Ваальса: а) для температуры ниже критической; 6) для температуры выше критической?

4. Сравните изотермы Ван-дер-Ваальса с экспериментальными кривыми для одного и того же газа.

5.Какой эффект Джоуля-Томсона называют положительным, какой отрицательным?

6. От каких параметров зависит температура инверсии? Как записать эту зависимость? Каков физический смысл температуры инверсии?

7. Что называют насыщенным паром? Чем определяется давление насыщенного пара?

8. Какой физический смысл имеют величины b, V-b, а/V², входящие в уравнение Ван-дер-Ваальса?

9. Для двух различных газов, взятых в равных количествах и имеющих одинаковые объемы и температуры, рассчитали давление по уравнению Ван-дер-Ваальса. Результаты сравнили с давлением идеального газа с такими же параметрами. Оказалось, что давление одного газа больше давления идеального газа, другое меньше. Чем объяснить полученные отличия в давлениях?

10.Зависимость давления от объема, полученная при решении уравнения Ван-дер-Ваальса, изображена на рис.1, экспериментальная кривая показана на рис.2. Чем объясняется различие в графиках?

Рис.1 Рис.2

12. В каком агрегатном состоянии находится вещество, если его состояние на графике (рис.2) определяется точками 1,2,3?

13.Какому физическому состоянию соответствуют участки ав, вб, dl кривой на рис. 1?

14.Что можно сказать о значениях заштрихованных площадей на рис.1?

15.Как с увеличением температуры вещества меняется ход графиков, приведенных на рис.1?

16.В замкнутом сосуде, содержащем некоторое вещество в двух фазах, поддерживается постоянное давление. Температура постепенно повышается от значения меньшего критического до значения большего критического. Начертите на координатной плоскости VT примерные графики процесса для случаев: а) давление равно критическому; б) давление больше критического; в) давление меньше критического. Считайте, что при температурах больших критической, вещество имеет свойства идеального газа.

17.Чем объясняется, что в процессе дросселирования при комнатной температуре водород нагревается, а кислород охлаждается?

18.Каков в опыте Джоуля-Томсона знак приращения внутренней энергии газа? Энтропии? Тепловой функции? (энтальпии)

19.Начертите экспериментальную изотерму процесса сжатия реального газа и объясните ход графика.

20.Каков смысл коэффициента в уравнении Ван-дер-Ваальса и как он выражается через размеры атомов?

21.Каков смысл коэффициента а в уравнении Ван-дер-Ваальса и как он определяется?

22.Начертите изотерму Ван-дер-Ваальса и укажите, каким состояниям соответствуют различные участки изотермы?

23.Что такое критическая температура?

24.3а счет каких физических факторов сжимаемость реального газа при малом давлении больше, чем идеального, а при большом — меньше?

25.Какие соображения позволяют выбрать давление, при котором должна быть проведена горизонтальная изотерма реального газа, соответствующая двухфазному состоянию?

26.Как наглядно объяснить зависимость знака дифференциального эффекта Джоуля-Томсона от давления газа?

27.Каким физическим условиям в газе соответствует точка инверсии дифференциального эффекта Джоуля-Томсона?

28.Чем свойства пара отличаются от свойств газа? При каких условиях к пару можно применить газовые законы?

29.От каких термодинамических параметров зависит внутренняя энергия газа

Ван-дер-Ваальса?

30.В чем заключается эффект Джоуля-Томсона? Каким уравнением описывается это явление?

31.В чем сущность процесса дросселирования газа? Является ли выпуск сжатого газа в пустоту процессом дросселирования? Как изменяется температура идеального газа при выпуске его в пустоту?

32.В чем заключается явление Джоуля-Томсона? Каким уравнением описывается это явление?

33.Какая температура называется температурой инверсии Джоуль-Томсон эффекта?

34.Какие значения должны иметь величины а и b в уравнении Ван-дер-Ваальса, чтобы газ всегда охлаждался при дросселировании?

35.Какие участки кривой Ван-дер-Ваальса соответствует нестабильным и метастабильным состояниям? Объясните смысл и возможность осуществления этих состояний.

36.Что такое перегретая жидкость? Укажите ее область на изотерме Ван-дер-Ваальса.

37.Что такое дросселирование газа? Почему процесс дросселирования в идеальном газе не сопровождается изменением температуры, а в не идеальном газе сопровождается?

38. Что происходит с газом Ван-дер-Ваальса с поправкой а =0 в опыте Джоуля-Томсона, газ нагревается, охлаждается или температура газа не меняется?

39. Что происходит с газом Ван-дер-Ваальса с поправкой в =0 в опыте Джоуля-Томсона, газ нагревается, охлаждается или температура газа не меняется?

40.Какое значение имеет приращение внутренней энергии газа ΔU в опыте Джоуля-Томсона для случая, когда начальное состояние характеризуется точкой, лежащей па кривой инверсии, - положительное, отрицательное или не изменяется?

41.Как изменяются температуры водорода и кислорода в результате дросселирования при комнатной температуре?

42. Получите приведенное уравнение Ван-дер-Ваальса. В чем его преимущество?

43. Каким выражением определяется критическая температура газа Ван-дер-Ваальса?

44. Каким выражением определяется критический объем газа Ван-дер-Ваальса?

45. Каким выражением определяется критическое давление газа Ван-дер-Ваальса?

46. Какому выражению соответствует связь между давлением, объемом и температурой киломоля газа Ван-дер-Ваальса в критической точке?

48. Найти приращение энтропии ΔS киломоля газа Ван-дер-Ваальса при изотермическом расширении от объема V₁ до объема V₂. Считать, что поправка Ван-дер-Ваальса в известна.

Глава 6. Жидкое состояние

Строение жидкостей

Жидкое состояние, занимая промежуточное положение между газом и кристаллами, сочетает в себе некоторые черты обоих этих состояний. В частности, для жидкостей, как и для кристаллических тел, характерно наличие определенного объема, а вместе с тем, жидкость, подобно газу, принимает форму того сосуда, в котором она находится. Известно, что для кристаллического состояния характерно упорядоченное расположение частиц, в газах, наоборот, царит полный хаос. В жидкостях, как показывают рентгенографические исследования, расположение частиц является также промежуточным. В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится все менее упорядоченным и довольно быстро порядок в расположении частиц полностью исчезает. В кристаллах имеет место дальний порядок - упорядоченное расположение частиц по отношению к любой частице наблюдается в пределах всего объема.

Из-за отсутствия дальнего порядка жидкости (за исключением жидких кристаллов) не обнаруживают анизотропии, характерной для кристаллов с их правильным расположением частиц.

В жидкостях с удлиненными молекулами наблюдается одинаковая ориентация молекул в пределах значительного объема, чем обуславливается анизотропия оптических и некоторых других свойств. Такие жидкости получили название жидких кристаллов. У них упорядочена только ориентация молекул, взаимное же расположение молекул, как и в обычных жидкостях, дальнего порядка не обнаруживают. Из-за того, что в жидкости отсутствует дальний порядок, а молекулы жидкости испытывают значительные силы межмолекулярного взаимодействия, его теория гораздо менее развита, чем теория кристаллического, и, особенно, газообразного состояний.

Значительная заслуга в разработке ряда проблем теории жидкого состояния принадлежит ученому Я.И.Френкелю. Согласно Френкелю, тепловое движение в жидкостях имеет следующий характер. Каждая молекула в течение некоторого времени колеблется около определенного положения равновесия. Время от времени молекула меняет место равновесия, скачком перемещаясь в новое положение, отстоящее от предыдущего на расстоянии порядка размеров молекул. Таким образом, молекулы лишь медленно перемещаются внутри жидкости, пребывая часть времени около определенных мест. Время колебания молекул в этих местах, или так называемое время оседлой жизни зависит от температуры жидкости, резко убывая при повышении температуры. В связи с этим при повышении температуры сильно возрастает подвижность молекул, что, в свою очередь влечет за собой уменьшение вязкости жидкости.

Поверхностное натяжение

Поверхность жидкости, соприкасающейся с другой средой (собственным паром, какой-либо другой жидкостью или твердым телом) находится в особых условиях по сравнению с остальной массой жидкости. Возникают эти особые условия потому, что молекулы пограничного слоя жидкости в отличие от молекул в ее глубине окружены молекулами той же жидкости не со всех сторон. Часть соседей поверхностных молекул - это частицы второй среды, с которой жидкость граничит. Эта среда может отличаться от жидкости, как природой, так и плотностью частиц. Имея же разных соседей, молекулы поверхностного слоя и взаимодействуют с ними различным способом. Поэтому силы, действующие на каждую молекулу в этом слое, оказываются неуравновешенными, существует некоторая равнодействующая сила, направленная либо в сторону объема жидкости, либо в сторону объема граничной с ней среды. Вследствие этого перемещение молекулы из поверхностного слоя в глубь жидкости или вглубь среды, с которой она граничит, сопровождается совершением работы. Равнодействующая всех сил, действующих на молекулы внутри жидкости равно нулю, поэтому их перемещение не сопровождается работой. Величина и знак работы совершаемой при перемещении молекул поверхностного слоя зависит от соотношения между силами взаимодействия молекул этого слоя со "своими" же молекулами и с молекулами второй среды. В случае, когда жидкость граничит со своим собственным паром, сила, испытываемая молекулами поверхностного слоя, направлена внутрь жидкости. Это связано с тем, что плотность молекул в жидкости намного больше, чем в насыщенном паре над жидкостью, соответственно, сила притяжения молекулами поверхностного слоя со стороны молекул жидкости больше, чем со стороны молекул пара.

Молекулы поверхностного слоя, перемещаясь во внутрь жидкости, совершают положительную работу. Наоборот, переход молекул из объема жидкости к поверхности сопровождается отрицательной работой, т.е. требует затраты внешней работы. Если поверхность жидкости увеличивается, это значит, что некоторое количество молекул из объема жидкости переходит на поверхность. Для этого надо затратить внешнюю работу. Таким образом, увеличение поверхности жидкости сопровождается отрицательной работой. Наоборот, при сокращении поверхности совершается положительная работа. Если при постоянной температуре обратимым путем изменить поверхность жидкости на бесконечно малую величину 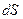, то необходимая для этого работа равна

.

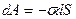Знак "минус" показывает, что при увеличении поверхности 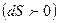совершается отрицательная работа. Коэффициент 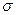называется коэффициентом поверхностного натяжения.

Из сказанного выше следует, что молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами, находящимися в объеме жидкости, потенциальной энергией 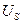, которая измеряется работой, которую могут совершить молекулы поверхности, перемещаясь внутрь жидкости под действием сил притяжения со стороны молекул в объеме жидкости.

Поскольку энергия 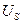обязана своим происхождением наличию поверхности жидкости, то она должна быть пропорциональна площади 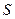поверхности жидкости

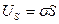. (6.1)

Тогда изменение поверхности 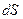повлечет за собой изменение потенциальной энергии 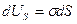, которая сопровождается работой 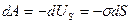. Если изменение поверхности 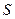происходит при постоянной температуре, то совершаемая работа равна изменению свободной энергии поверхности

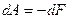. (6.2)

В

Таким образом, поверхность жидкости обладает избыточной по сравнению с остальной массой жидкости потенциальной энергией. Рассмотрим, к чему это приводит. Известно, что всякая система в состоянии равновесия имеет минимальное значение энергии. Из формулы (6.1) следует, что поверхность жидкости в состоянии равновесия должна иметь минимальное значение поверхности. Это в свою очередь означает, что должны существовать силы, препятствующие увеличению поверхности, т.е. стремящиеся сократить эту поверхность. Эти силы должны быть направлены вдоль самой поверхности, по касательной к ней. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие эту поверхность. Эти силы называются силами поверхностного натяжения.

Рассмотрим пример. Если проволочную рамку, одна из сторон которой подвижна (см. рис.1) опустить в мыльный раствор, то вся она затянется пленкой жидкости. Силы поверхностного натяжения принуждают пленку сокращаться, и подвижная перекладина АВ вслед за пленкой перемещается вверх. Чтобы сохранить ее в равновесии к перекладине нужно приложить силу Р в виде груза. Таким образом, сила поверхностного натяжения, действующая в пленке, перпендикулярна к линии АВ, которая в данном случае и является линией раздела. Такие же силы действуют на другие стороны рамки. Но здесь они уравновешиваются силами притяжения жидкости к веществу жесткой рамки. Описанный опыт может быть использован для определения численного значения коэффициента поверхностного натяжения жидкости. Действительно, поверхностная сила 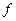, с учетом того, что пленка имеет две поверхности, равно при равновесии весу груза Р, т.е.

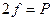
или

.

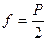Если под действием этой силы перекладина, увлекаемая пленкой, переместилась на расстояние 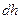из положения АВ, то работа, совершенная силой равна 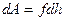. Эта работа как видно из (6.2) равно уменьшению свободной энергии пленки, которая равна:

.

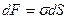В данном случа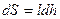е , где 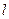- длина рамки. Отсюда

.

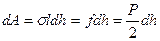Отсюда

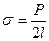. (6.3)

Из (6.3) следует, что коэффициент поверхностного натяжения может быть определен как величина, равная силе, действующей по касательной к поверхности жидкости, приходящейся на единицу длины линии раздела.