Показатели анализа рядов динамики
Анализ рядов динамики осуществляется с помощью следующих показателей: уровень, абсолютный прирост, темп роста, темп прироста и абсолютное значение одного процента прироста.
Уровень ряда - это первичные значения показателя, отображающие непосредственно уровень развития явления определённую дату или за определённый период. Различают начальный, конечный и средний уровень ряда. Начальным называют первый член ряда динамики, а конечным – последний его член. Средний уровень интервального ряда динамики рассчитывается при помощи средней арифметической простой.
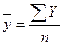 ,
,
где n - число уровней.
Средний уровень моментного ряда динамики рассчитывается по различным формулам в зависимости от имеющихся данных:
а) если есть точные сведения о моменте изменения уровня ряда, то используется формула средней арифметической взвешенной
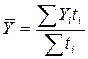 .
.
Пример 1
На 1 января 1995 года число рабочих цеха было равно 100 человек; 10 января приняли на работу 2 рабочих, 15 января уволили 3 рабочих, 25 января приняли 1 рабочего. До конца января изменений не было. Определить среднюю списочную численность рабочих цеха за январь 1995 года.
Таблица 6
Расчётная таблица
| Дата | Изменение в числе рабочих | 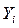 | Продолжительность периода | 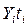 |
| 1.01 | ||||
| 10.01 | +2 | |||
| 15.01 | -3 | |||
| 25.01 | +3 | |||
| Итого |
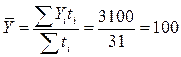 рабочих.
рабочих.
б) если нет точных сведений о моменте изменения уровня, то расчёт среднего уровня осуществляют по формуле средней арифметической взвешенной из средних величин. Эти средние за период между двумя моментами изменения ряда находят как полусуммы уровней ряда на начало и конец данного периода.
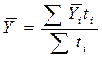 .
.
Пример 2
Имеются следующие данные о списочной численности рабочих:
на 1.01 - 100 рабочих
10.01 - 102 рабочих
15.01 - 99 рабочих
25.01 - 100 рабочих
31.01 - 104 рабочих
Определить среднесписочную численность рабочих за январь.
Таблица 7
Расчётная таблица
| Дата | 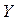 | 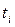 | 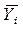 | 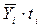 |
| 1.01 | ||||
| 10.01 | 101,0 | |||
| 15.01 | 101,5 | 507,5 | ||
| 25.01 | 99,5 | |||
| 31.01 | ||||
| Итого | 3125,5 |
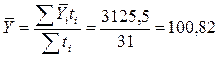 чел.
чел.
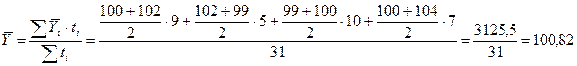 чел.
чел.
в) если нет точных сведений о моменте изменения ряда и промежутки между датами, на которые есть сведения, равны, то используется формула средней хронологической, которая является частным случаем средней арифметической взвешенной из средних величин.
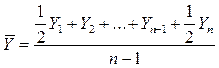 .
.
Пример 3
Имеются следующие данные о списочной численности рабочих за ноябрь:
1.11 - 100 чел.
11.11 - 110 чел.
21.11 - 108 чел.
1.12 - 112 чел.
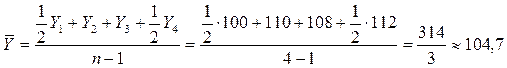 чел.
чел.
или
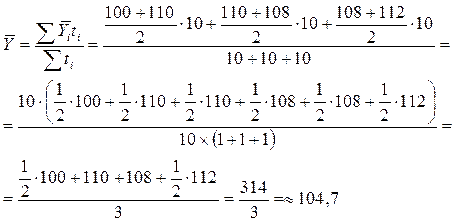
Абсолютным приростом в статистике называется разность двух уровней ряда динамики. Он характеризует размер увеличения или уменьшения уровня явления в абсолютных величинах за определённый период времени. Обозначается абсолютный прирост - 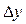 . Абсолютные приросты могут быть положительными, отрицательными и нулевыми.
. Абсолютные приросты могут быть положительными, отрицательными и нулевыми.
Рассчитывают цепные и базисные абсолютные приросты. Цепные абсолютные приросты показывают изменение данного уровня ряда по сравнению с предыдущим.
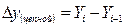
Базисные абсолютные приросты показывают изменение данного уровня по сравнению с начальным уровнем ряда.
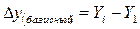
Сумма цепных 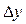 равна соответствующему базисному абсолютному приросту
равна соответствующему базисному абсолютному приросту 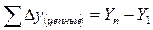 , где
, где 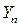 - последний уровень ряда динамики.
- последний уровень ряда динамики.
Средний абсолютный прирост рассчитывают по формулам:
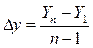 ;
; 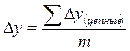 ,
,
где m - число цепных 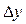 .
.
Темп роста представляет собой отношение двух уровней ряда, выраженное в процентах или коэффициентах. Он характеризует интенсивность развития явления во времени.
Цепные темпы роста вычисляются по формуле:
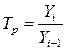 или
или 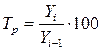
Базисные: 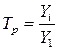 или
или 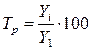
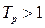 показывает во сколько раз увеличился данный уровень ряда по сравнению с предыдущим или базисным уровнем.
показывает во сколько раз увеличился данный уровень ряда по сравнению с предыдущим или базисным уровнем. 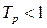 показывает, какую часть составляет данный уровень от предыдущего или базисного уровня. На основе вычисленных цепных темпов роста можно вычислить коэффициенты ускорения, т.е. отношения последующих цепных темпов роста к предыдущему. Коэффициент ускорения характеризует интенсивность изменения темпов роста.
показывает, какую часть составляет данный уровень от предыдущего или базисного уровня. На основе вычисленных цепных темпов роста можно вычислить коэффициенты ускорения, т.е. отношения последующих цепных темпов роста к предыдущему. Коэффициент ускорения характеризует интенсивность изменения темпов роста.
Между базисными и цепными темпами роста существует следующая взаимосвязь: произведение цепных темпов роста равно соответствующему базисному темпу роста.
Средний темп роста рассчитывается по формуле средней геометрической:
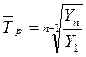 или
или 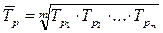 ,
,
где m - число цепных темпов роста (выраженных в коэффициентах).
Темп прироста показывает, на сколько процентов увеличился или уменьшился данный уровень по сравнению с предыдущим или базисным.
Цепные темпы прироста вычисляются по формулам:
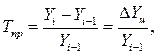
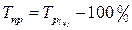
Базисные: 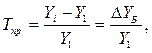
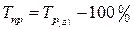
Средний темп прироста вычисляется:
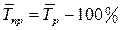 .
.
Абсолютное значение 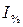 прироста - это отношение цепного абсолютного прироста к цепному темпу прироста, выраженному в процентах.
прироста - это отношение цепного абсолютного прироста к цепному темпу прироста, выраженному в процентах.
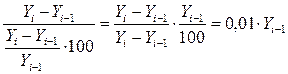 ,
,
т.е. абсолютное значение 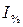 прироста равно одной сотой доле предыдущего уровня.
прироста равно одной сотой доле предыдущего уровня.
Каждый показатель динамики имеет свой смысл, поэтому анализ динамики какого - либо явления требует параллельного использования всех показателей динамики.
Вычисление показателей анализа ряда динамики покажем на следующем примере.
Объём производства на предприятии характеризуется следующими данными:
| ГОДЫ | ||||||
| Производство продукции (тыс.т.) | 1571,3 | 1649,3 | 1726,5 | 1790,3 | 1855,0 | 1895,6 |
Цепные абсолютные приросты = 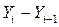
2001- 1649,3-1571,3=78,0 тыс. т.
2002- 1726,5-1649,3=77,2 тыс. т.
2003- 1790,3-1726,5=63,8 тыс. т.
2004- 1855,0-1790,3=64,7 тыс. т.
2005- 1895,0-1855,0=40,6 тыс. т.
Базисные абсолютные приросты = 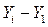
1991- 1649,3-1571,3=78,0 тыс. т.
1992- 1726,5-1573,3=155,2 тыс. т.
1993- 1726,5-1571,3=219,0 тыс. т.
1994- 1855,0-1571,3=283,7 тыс. т.
1995- 1895,0-1571,3=324,3 тыс. т.
78,0+77,2+63,8+64,7+40,6=324,3 тыс. т.
Цепные темпы роста = 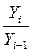
2001г. - 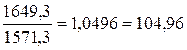 %
%
2002г. - 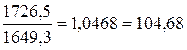 %
%
2003г. - 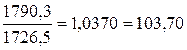 %
%
2004г. - 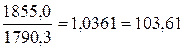 %
%
2005г. - 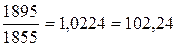 %
%
Базисные темпы роста = 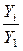
2001г. - 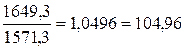 %
%
2002г. - 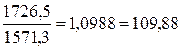 %
%
2003г. - 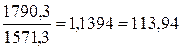 %
%
2004г. - 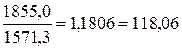 %
%
2005г. - 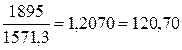 %
%
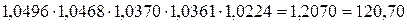 %
%
Цепные и базисные темпы прироста вычислим как разницу между соответствующим темпом роста и 100%. Они будут равны:
цепные - 4.96%; 4,68%; 3,70%; 3,81%; 2,24%.
базисные - 4,96%; 9,88%; 13,94%; 18,06%; 20,7%.
Абсолютное значение 1% прироста = 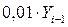
2001г. - 15,713 тыс. т.
2002г. - 16,493 тыс. т.
2003г. - 17,265 тыс. т.
2004г. - 17,903 тыс. т.
2005г. - 18,550 тыс. т.
Уровни ряда динамики в нашем примере имеют ясно выраженную тенденцию роста (увеличение базисных абсолютных приростов, темпов роста и прироста). При этом скорость и интенсивность роста снижается (уменьшение цепных показателей).
Вычисленные показатели представим в таблице:
| Год | Произ-во продукции тыс. т. | Абсолютные приросты, тыс. т. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. т. | |||
| цеп. | базис. | цеп. | базис. | цеп. | базис. | |||
| 1971,3 | - | - | - | 105,70 | - | - | - | |
| 1642,З | 78,0 | 78,0 | 100,0 | 113,94 | 4,96 | 4,96 | 15,713 | |
| 1726,5 | 77,2 | 155,2 | 104,96 | 103,61 | 4,68 | 9,88 | 16,493 | |
| 1790,3 | 63,8 | 219,0 | 104,96 | 118,06 | 3,70 | 13,94 | 17,265 | |
| 1855,0 | 64,7 | 283,7 | 104,68 | 102,24 | 3,61 | 18,06 | 17,903 | |
| 1895,6 | 40,6 | 324,3 | 109,88 | 120,70 | 2,24 | 20,70 | 18,550 |
Изучение основной тенденции развития
Основная тенденция развития (тренд) обусловлена постоянно действующими факторами. Воздействие случайных факторов проявляется периодически и вызывает колебания уровней рядов динамики. Задача статистики - выявить и измерить основную тенденцию развития. Решение этой задачи осуществляется с помощью следующих методов: укрупнение интервалов, метод скользящей средней, аналитическое выравнивание.
Метод укрупнения интервалов состоит в том, что данные интервалы ряда динамики заменяют более крупными (например, месячные - квартальными, годичные - пятилетними), и эти укрупненные интервалы характеризуют суммарными или средними величинами.
Пример.
Имеются следующие данные о производстве продукции, тыс. т.
| Месяц года | Производство продукции | Месяц года | Производство продукции | Месяц года | Производство продукции | Месяц года | Производство продукции |
| I П Ш | IV V VI | VII VIII IX | X XI XII |
Тенденция данного динамического ряда выражена нечетко. Для ее выявления укрупним интервалы до квартальных, в результате чего получим следующие результаты.
| Квартал | Производство продукции, тыс. шт. | |
| суммарное | среднемесячное | |
| I П Ш IV | 151+146+152=449 151+154+145=450 149+147+155=451 153+146+154=453 | 449:3=149,7 450:3=150,0 451:3=150,3 453:3=151,0 |
Как видим, преобразованные ряды динамики из суммарных величин и средних четко выражают тенденцию роста производства продукции.
Метод скользящей средней основан на свойстве средней погашать случайные отклонения от общей закономерности. Расчет скользящей средней осуществляется по средней арифметической простой из заданного числа уровней ряда (шага), с отбрасыванием при вычислении каждой новой средней предыдущего уровня и присоединением следующего. В результате расчет средней как бы скользит от начала ряда динамики к его концу. При нечетном шаге каждая вычисленная скользящая средняя соответствует реальному интервалу (моменту) времени, находящемуся в середине шага, а число сглаженных уровней меньше первоначального числа уровней на величину шага скользящей средней, уменьшенного на единицу.
Если шаг скользящей средней выражен четным числом, то полученные скользящие средние центрируют. Операция центрирования заключается в повторном скольжении с шагом, равным двум. Число уровней сглаженного ряда будет меньше на величину шага скользящей средней.
Используя данные приведенного выше примера проведем сглаживание ряда методом скользящей средней:
а) трехмесячной
| Месяцы | Производство продукции (тыс. шт.) | Расчет скользящих средних | Сглаженные уровни ряда |
| Январь | - | - | |
| Февраль | (151+146+152):3 | 149,7 | |
| Март | (146+152+151):3 | 149,7 | |
| Апрель | (152+151+154):3 | 152,3 | |
| Май | (151+154+142):3 | 149,0 | |
| Июнь | (154+145+149):3 | 149,3 | |
| Июль | (145+149+147):3 | 147,0 | |
| Август | (149+147+155):3 | 150,3 | |
| Сентябрь | (147+155+153):3 | 151,7 | |
| Октябрь | (155+153+146):3 | 151,3 | |
| Ноябрь | (153+146+154):3 | 151,0 | |
| Декабрь | - | - |
б) четырехмесячной
| Месяцы | Производство продукции, тыс. т. | Расчет скользящих средних | Центрирование скользящих средних | Сглаженные уровни ряда |
| Январь | - | |||
| Февраль | - | |||
| Март | (151+146+152+151):4=150,00 (146+152+151+154):4=150,75 (152+151+154+145):4=150,50 (151+154+145+149):4=148,25 (154+145+149+147):4=148,75 (145+149+147+155):4=149,00 (149+147+155+153):4=151,00 (147+155+153+146):4=150,25 (155+153+146+154):4=152,00 | (150,00+150,75):2 | 150,385 | |
| Апрель | (150,75+150,50):2 | 150,625 | ||
| Май | (150,50+148,25):2 | 149,375 | ||
| Июнь | (148,25+148,75):2 | 148,500 | ||
| Июль | (148,75+149,00):2 | 148,875 | ||
| Август | (149,00+151,00):2 | 150,000 | ||
| Сентябрь | (151,00+150,25):2 | 150,625 | ||
| Октябрь | (150,25+152,00):2 | 151,125 | ||
| Ноябрь | ||||
| Декабрь | - |
Аналитическое выравнивание ряда динамики. Изменение уровней ряда динамики с той или иной степенью точности может быть представлено в виде определенной математической формулы (функции), отражающей общую тенденцию развития (тренд). Аналитическое выравнивание ряда динамики может быть осуществлено либо по формуле прямой линии, либо по параболе второго порядка, либо по показательной (экспонентной) функции.
Выбор формулы уравнения производится на основе теоретического анализа законов развития, характера динамики изучаемого явления.
Если изменение уровней ряда характеризуется равномерным увеличением (уменьшением) уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии:
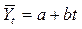 ,
,
где 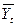 - выравненные, теоретические уровни ряда динамики, исчисленные по аналитическому уравнению;
- выравненные, теоретические уровни ряда динамики, исчисленные по аналитическому уравнению;
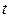 - показатель времени;
- показатель времени;
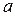 и
и 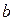 - параметры уравнения.
- параметры уравнения.
Если в результате анализа типа тенденции динамики установлена криволинейная зависимость с примерно постоянным ускорением, то форма тенденции выражается уравнением параболы второго порядка 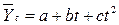
Если рост уровней ряда динамики происходит в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны, выравнивание ряда динамики ведется по показательной функции 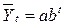
Выбор типа линии, выражающей тенденцию развития, можно произвести, используя графическое изображение ряда динамики (линейную диаграмму).
Методику аналитического выравнивания рассмотрим на следующем примере. Имеются следующие данные об изменении объёма строительно-монтажных работ по строительному управлению (в сопоставимых ценах).
| Годы | |||||||||
| СМР, д.е. | 63,5 | 69,8 | 64,7 | 70,8 | 77,5 | 82,4 | 86,1 | 83,3 | 85,9 |
Представим данные ряда динамики в виде линейной диаграммы.
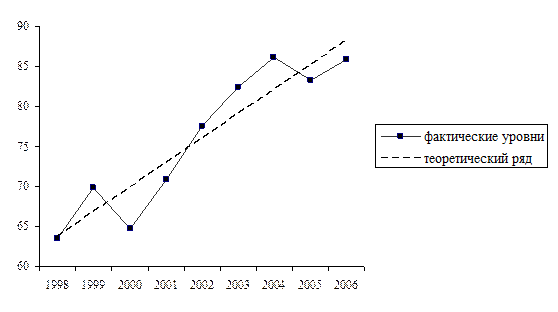
Рис. 1
Из графика видно, что в данном случае следует избрать для выравнивания уравнение прямой: 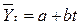
Параметры 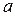 и
и 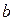 этой прямой определим по способу наименьших квадратов, решением следующей системы нормальных уравнений:
этой прямой определим по способу наименьших квадратов, решением следующей системы нормальных уравнений:
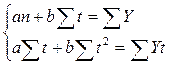 ,
,
где 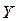 - фактические уровни ряда;
- фактические уровни ряда;
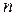 - число уровней ряда динамики;
- число уровней ряда динамики;
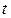 - условное обозначение времени.
- условное обозначение времени.
Если начало условного отсчета времени поместить в середину изучаемого периода, то 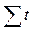 будет равна 0. Это значительно упростит решение данной системы, т.к. при
будет равна 0. Это значительно упростит решение данной системы, т.к. при 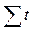 =0 она примет следующий вид:
=0 она примет следующий вид:
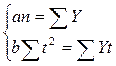
отсюда 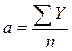 ,
, 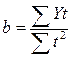 .
.
Расчеты необходимых значений для определения параметров 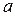 и
и 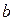 произведем в расчетной таблице.
произведем в расчетной таблице.
| Годы | Эмпирический ряд ( 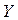 ) ) | Условное обозначение дат ( 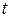 ) ) | 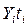 | 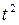 | Выравненный ряд динамики 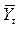 |
| 53,5 | -4 | -254 -209,4 -129,4 - 70,8 +82,4 +172,2 +149,9 +343,6 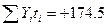 | 64,37 | ||
| 69,8 | -3 | 67,27 | |||
| 64,7 | -2 | 70,18 | |||
| 70,8 | -1 | 73,10 | |||
| 77,5 | 76,00 | ||||
| 82,4 | +1 | 78,91 | |||
| 86,1 | +2 | 81,82 | |||
| 83,3 | +3 | 84,72 | |||
| 85,9 | +4 | 87,63 | |||
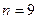 | 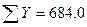 | 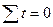 | 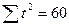 | 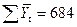 |
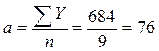 ;
; 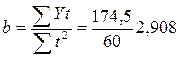
тогда уравнение прямой будет иметь вид: 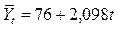
По этому уравнению найдем теоретические значения уровней ряда динамики и нанесем их на график, впишем в таблицу.
1887г. 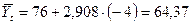
1988г. 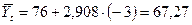
1989г. 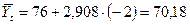 и т.д.
и т.д.
Правильность расчета выровненных уровней доказывает равенство 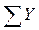 и
и 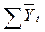 (684=684)
(684=684)
Параметр 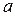 в данном случае соответствует величине срединного уровня теоретического ряда динамики (в точке времени принятого за начало отсчета при
в данном случае соответствует величине срединного уровня теоретического ряда динамики (в точке времени принятого за начало отсчета при 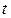 =0), параметр
=0), параметр 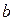 характеризует средний абсолютный прирост уровней ряда динамики за единицу времени
характеризует средний абсолютный прирост уровней ряда динамики за единицу времени 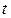 .
.
Если ряд динамики имеет четное число уровней, то условное обозначение времени производится следующим образом:
| Даты | ||||||
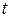 | -5 | -3 | -1 | +1 | +3 | +5 |
В этом случае значение параметра 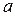 лишено реального смысла, а параметр
лишено реального смысла, а параметр 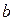 характеризует средний абсолютный прирост уровней ряда за половину периода. Используя определенное выше уравнение обшей тенденции развития явления (уравнение тренда), можно с достаточной точностью сделать прогноз на будущее (экстраполяция). Однако пользоваться экстраполяцией следует с большой осторожностью, только тогда, когда есть уверенность в том, что условия формирования уровней ряда динамики не изменяются.
характеризует средний абсолютный прирост уровней ряда за половину периода. Используя определенное выше уравнение обшей тенденции развития явления (уравнение тренда), можно с достаточной точностью сделать прогноз на будущее (экстраполяция). Однако пользоваться экстраполяцией следует с большой осторожностью, только тогда, когда есть уверенность в том, что условия формирования уровней ряда динамики не изменяются.
Нахождение неизвестного уровня внутри ряда динамики называют интерполяцией. Находят его путём определения средней величины из двух (иногда четырёх) членов ряда, непосредственно примыкающих к неизвестному члену ряда.
ИНДЕКСНЫЙ МЕТОД АНАЛИЗА
