Түбір жатқан аралықты анықтау әдісі

F(x)=0 (2.1)

Бірөлшемді сызықты емес теңдеу берілген. Мұндағы F(x) функциясы [a,b] кесіндісінде анықталған және үзіліссіз болсын.

Теорема1.1:[а,в] аралығында анықталған, үзіліссіз F(x) функциясының екі шеткі нүктелердегі мәндерінің таңбалары әр түрлі болса, яғни мына шарт орындалса f(a)*f(b)<0, онда осы аралықта (2.1)-теңдеудің түбірі бар және жалғыз болады.

Практикада кейде теореманың орындалуын функцияның мәндер кестесін құру арқылы да анықтайды. Функцияның анықталу облысы бойынша а нүктесін беріп, ол нүктедегі функция мәнін анықтайды, сосын һ қадаммен келесі нүктеге жылжып, сол нүктедегі функция мәнін анықтайды, сол сияқты бірнеше нүктедегі функция мәндерін анықтап, таңбасын салыстырады. Егер көрші нүктелерде функция әр түрлі таңба қабылдаса, сол аралықта жалғыз түбірі жатыр деп айтады.

1-мысал:

Берілген теңдеудің түбірін анықтау:

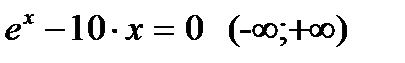
Теңдеудің түбірі жатқан аралықты аналитикалық тәсілмен табамыз: ол үшін функция туындысын тауып, оны нөлге теңестіру арқылы экстремумдарын анықтаймыз: 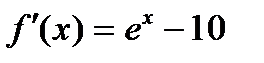, экстремумы: х₁=Ln10=2,3;

Экстремум нүктелеріндегі функция таңбасының 1-кестесін толтырамыз.

1-кесте- 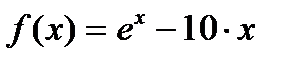функциясының таңбасын анықтау

Нүктелер		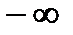2,3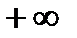
sign(f)	+	-	+

Функция таңбасының ауысуы ( 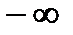; 2,3] және [2,3; 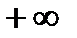) аралығында байқалды. Яғни осы аралықта теңдеудің түбірі бар.

Енді графиктік әдісті қарастырайық. Ол үшін теңдеуді мына түрлерге жіктейміз, себебі функция күрделі, трансцендентті, бірден графигін құруға болмайды: 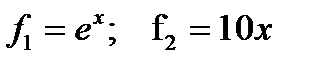. Екі функцияның графигін саламыз, екеуінің қиылысқан нүктесі теңдеудің түбірі болып табылады (1-сурет). Қиылысу нүктелерінің аймақтарын анықтаймыз.

1-сурет- 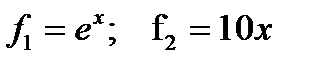функцияларының графиктері

Бірінші түбірі [0,1] аралығында, ал екінші түбірі [2,6] аралығында жататыны суретте көрініп тұр. Енді осы аралықтағы қай нүкте (2.1)-ші теңдеуді қанағаттандыратынын анықтаймыз.

3.2 Теңдік түбірін анықтау әдістер

Ньютон әдісі

Алдыңғы әдістерге қарағанда бастапқы жуықтау дұрыс таңдалынып алынса Ньютон әдісі тез жинақталады. Бұл әдіске қатысты теореманы келтіре кетейік:

Теорема 1.3.: f(x) функциясы [a,b] аралығында анықталған және екі ретті туындысы бар, осы аралықта түбір жатыр f(a)*f(b)<0, туындылардың таңбалары осы аралықта тұрақты болса f(x)*f^'(x)>0, онда f(x₀)*f^''(x₀)>0 теңсіздігін қанағаттандыратын 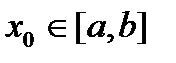бастапқы жуықтаудан бастап (2.1)-ші теңдеуді қанағаттандыратын [a,b]-да жататын жалғыз шешімге жинақталатын 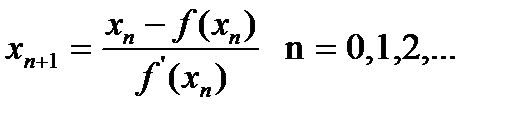итерациялық тізбек құруға болады.

Ньютон әдісінің геометриялық мағынасы: координаталары (x_n;f(x_n)) , болатын нүктеден қисыққа жанама жүргізсек, оның ох өсімен қиылысу нүктесі теңдеудің түбіріне х_n+1 – кезекті жуықтау болып табылады.

Түбірге n-ші жуықтаудың қателігін бағалау үшін келесі теңсіздіктің орындалуын қадағалау керек: 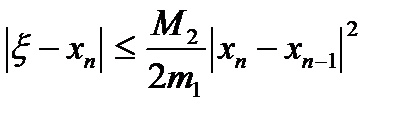. Мұндағы М₂ – функцияның екінші ретті туындысының аралықтағы максимумы, m₁- минимумы. Егер, 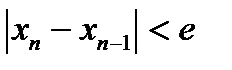болса, онда 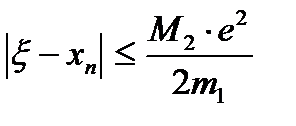болады, яғни түбірге дұрыс жуықталынса, әр итерациядан кейін кезекті жуықтаудың ондық таңба саны екіге артады да процесс тез жинақталады. Егер түбірді берілген е дәлдікпен табу керек болса, итерациялық процесті 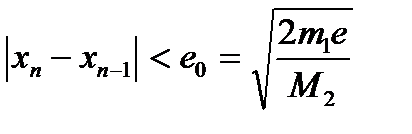шарты орындалғанша жалғастырамыз.

Бұл біртіндеп жуықтау әдісі деп аталады. Әдістің жинақталу жылдамдығы х₀ бастапқы нүктені дұрыс таңдауға байланысты. Егер итерация процесінде функцияның туындысы нөлге тең болса, қисыққа жүргізілген жанама 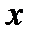осіне параллель болса, онда бұл әдісті қолдану қиындайды. Сол сияқты функцияның екінші ретті туындысының мәні шексіз үлкен болса және функцияның өзі бірінші ретті туындысы нөлге тең болса, онда шыққан түбірлер еселі болып, жинақталмауы мүмкін. Бұл әдісті қолдану үшін 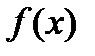функциясы үзіліссіз және дифференциалданған болуы керек.

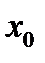бастапқы жуықтауды таңдалынған уақытта құрылатын тізбек монотонды кемімелі болуы керек.

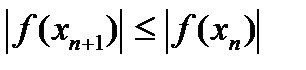
Алгоритмі:

1 Қисықтың бойынан қандайда бір 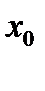нүктесін таңдап, осы нүкте арқылы қисыққа жанама жүргізіледі.

2 Жанама 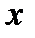осін қиған кезде табылған нүктенің мәні мына формуламен есептелінеді.

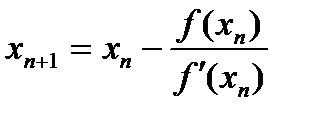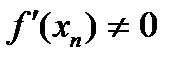, (2.5)

Табылған нүктедегі функцияның мәні нөлге өте жуық болса, онда сол нүкте (2.1) теңдеудің түбірі, болмаса процесс жалғасады.

Егер түбірлер еселі болса, ол еселікті 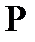деп белгілейік.

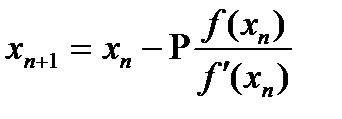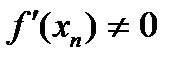, (2.6)

Хорда әдісі

Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез жинақталады.

Алгоритмі:

1 х_n , x_n+1 аралығында f (x) және f (x_n+1) функцияларының таңбасы бір біріне қарама-қарсы және түбірі бар болсын.

2 Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен қиылысқан нүктесін мына формуламен анықтаймыз.

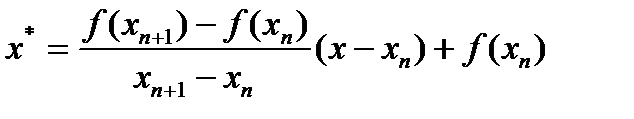(2.4)

Егер f(a)>0 шарты орындалса, а нүктесі тұрақты болады да 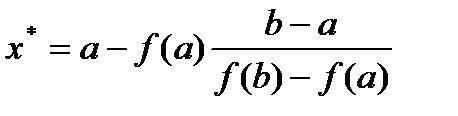формуласымен есептеледі

Егер f(b)>0 шарты орындалса, b нүктесі тұрақты болады да 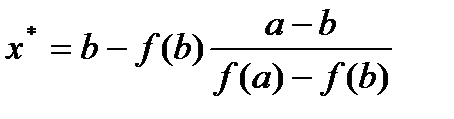формуласымен есептеледі

3 х^* нүктесіндегі функция мәнін F(x^*)-ны есептеу. Оның таңбасын екі шеткі нүктедегі функцияның таңбасымен салыстырылады. Егер f (x_n) және f(x^*) функциясының таңбасы бірдей болса, онда хорданы x_n+1 және x^* нүктесі арқылы жүргізіледі. Оның мәнін (2.4) формуламен табады. Егер f(x_n+1) мен f(x^*) функцияның таңбалары бірдей болса, онда хорданы x_n және x^* нүктесі арқылы жүргізіледі. Шыққан нүктенің мәні (2.4) формуламен есептелінеді.

4 x^* нүктедегі мәнін есептеп, мәні нөлге жуық болса 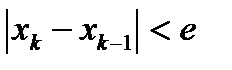, онда x^* нүктесі (2.1) теңдеудің түбірі деп аталады. Егер нөлге жуық болмаса, онда процесс жалғасады.

Алдындағы мысал үшін программасы келесідей болады:

Жай итерация әдісі

Бұл әдісті қолдану үшін (2.1)-ші теңдеудің сызықты мүшесі айшықталып мына түрге келтіру керек:

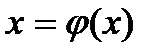(2.3)

Сосын теңдеудің түбіріне кез келген Х₀ бастапқы жуықтау беріп 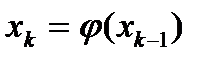k=1,2,… формуласымен х₁, х₂,…,х_n нүктелер тізбегін құрамыз. Бұл тізбек x=z түбіріне жинақталуы керек. Егер limX_k=z болса, онда z нүктесі 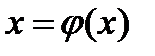теңдеуінің түбірі бола алады. Итерация әдісінің жинақтылық шарты 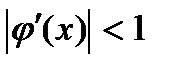және бастапқы жуықтау кез келген болады. Итерациялық процесс берілген дәлдікке жетуі үшін 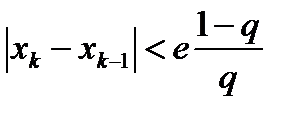шарты орындалуы керек.

Итерациялық тізбектің жинақтылығы теореманың ([1] қараңыз) шарттарымен де тексерілуі керек:

Теорема1.2.:

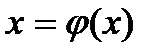теңдеуінің [a,b] аралығында жалғыз түбірі бар және келесі шарттар орындалсын:

1 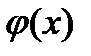функциясы [a,b] аралығында анықталған және дифференциалданады;

2 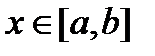үшін ;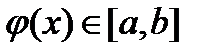

3 барлық 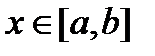үшін 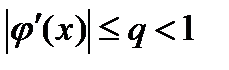болатындай q саны табылсын,

онда 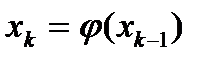, (k=1,2,…) итерациялық тізбегі 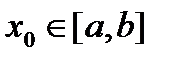кез келген бастапқы жуықтауда жинақталады.