Требования , предъявляемые к системам аксиом

Непротиворечивость системы аксиом

Система аксиом называется непротиворечивой, или совместной, если в теории 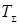этой системы невозможно доказать какое–нибудь утверждение А и его отрицание ùА. В противном случае система аксиом называется противоречивой.

Теория 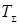, содержащая вместе с некоторым утверждением АÎ 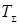и отрицание этого утверждения ùАÎ 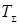называется не классической теорией. С точки зрения "здравого смысла" такая теория абсурдна, так как в мире "реальных вещей" некоторое свойство А "выражает" отношение этих реальных вещей и не может одновременно "не выражать" это отношение.

Теоретическая проверка совместности системы аксиом, основанная на непосредственном определении совместности, затруднительна. Действительно, пусть мы доказали утверждения А₁,А₂,...,А_n теории 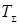и пусть отрицание этих свойств ùА₁,..., ùА_n невозможны в 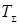. Где гарантия, что не найдется свойство А_n+1 , которое доказуемо вместе со своим отрицанием ùА_n+1 в теории 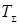? Такой гарантии нет, поскольку перебрать все возможные утверждения некоторой теории практически невозможно. Например, евклидова геометрия, согласно работе профессора Гарвардского университета Гаррета Биркгоффа [10], основанная на 20 аксиомах Гильберта, включает около 20.000 утверждений, получаемых логическим путем. Ясно, что нет никакой возможности проверить на непротиворечивость все эти 20.000 утверждений, составляющий предмет геометрической теории 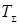={ А₁,А₂,...,А_20.000 }.

Мы уже говорили, что с точки зрения здравого смысла противоречивая система аксиом не должна допускать никакой реализации или модели (кроме, быть может, мыслимой модели), так как ни одно свойство в реальной модели не может иметь место вместе со своим отрицанием. Отсюда легко получаем следующее достаточное условие совместности.

Система аксиом Т совместна или непротиворечива, если существует хотя бы одна реализация R(T) этой системы.

Доказательство. Пусть 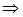А и Т 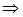ùА. Тогда реализация R(T) содержит свойство А и его отрицание, что невозможно в непротиворечивой реализации.

Вывод 1

Непротиворечивость всякой системы аксиом Т сводится к существованию хотя бы одной априорно не противоречивой реализации.

В качестве примера обратимся к трехмерной евклидовой геометрии. Так как одной из ее реализаций является арифметическая модель R³ (координатная модель), то евклидова геометрия непротиворечива, если непротиворечива арифметика действительных чисел. Таким образом, вопрос о непротиворечивости евклидовой геометрии сводится к вопросу о непротиворечивости арифметики действительных чисел.

Если в качестве реализации евклидовой геометрии рассматривать окружающий нас мир, то непротиворечивость этой геометрии будет сведена к опытной проверке. Однако расширение границ опыта в конце ХІХ – начале ХХ столетия привело к открытию неевклидовых геометрий в мире электромагнитных явлений, в мире гравитации. Так возникла специальная теория относительности, которая построена на законах неевклидовой геометрии, связанной с геометрией Лобачевского.

В качестве второго примера рассмотрим планиметрию Лобачевского. Она имеет реализацию Пуанкаре L₂, см. §5. В свою очередь L₂ имеет арифметическую модель: {(x,y); y>0} –"точки", {(x–a)²+y²=k² ,y>0} – "прямые", и так далее. Следовательно, вопрос о непротиворечивости планиметрии Лобачевского сводится, как и в случае евклидовой геометрии, к непротиворечивости арифметики.