ЛЕКЦИЯ № 15. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Вопрос 15.1. Градиент и производная по направлению функции нескольких переменных.

Определение 15.1. Векторным полем называется закон, по которому каждой точке X из некоторого множества M арифметического пространства 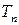ставится в соответствие один и только один вектор.

Определение 15.2. Градиентом функции нескольких переменных 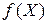называется векторное поле, определяемое по закону

.

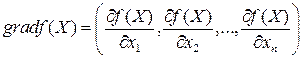Для функций 2-х и 3-х переменных градиент можно записать соответственно в виде

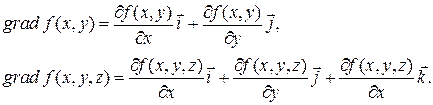
Замечание 15.1. Удобно точку X рассматривать как n‑мерный вектор .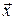

Градиент вектора обладает следующими двумя свойствами:

Свойство 15.1. Если 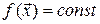, то .

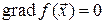Доказательство очевидно.

Свойство 15.2. (линейность градиента). Пусть даны два векторных поля 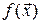и 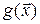, которые имеют градиент в точке 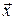, тогда

,

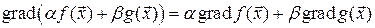где 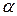и 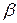‑ действительные числа.

Доказательство. Доказательство основано на свойстве линейности частных производных

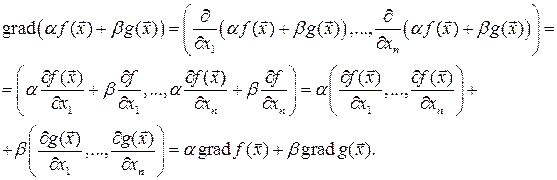
Конец доказательства.

Определение 15.3. Производной по направлению, заданным единичным вектором 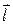, в точке 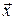от функции нескольких переменных 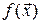называется величина

.

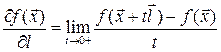Связь между градиентом и производной функцией по направлению 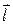определяется теоремой

Теорема 15.1. Если в точке 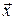функция 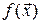дифференцируема, то

.

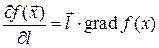где 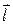‑ вектор единичной длины.

Доказательство. Пусть 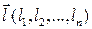приращение аргумента, тогда полное приращение дифференцируемой функции равно

,

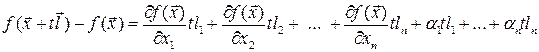где 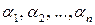‑ бесконечномалые функции при 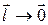. Так как

,

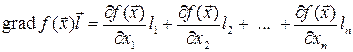то полное приращение функции равно

.

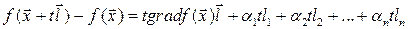Отсюда следует доказываемая формула.

Конец доказательства.

Рассмотрим свойства производной по направлению

Свойство 15.1.Если 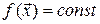, то .

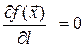Доказательство очевидно.

Свойство 15.2. Изменение вектора направления на противоположный меняет знак производной по направлению

.

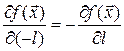Доказательство. Формула следует из равенства

.

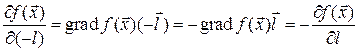Конец доказательства.

Свойство 3. (линейность производной по направлению). Пусть даны два дифференцируемых векторных поля 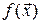и 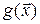, тогда

,

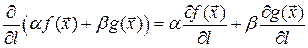где 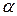и 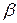‑ действительные числа.

Доказательство. Из теоремы 15.1 следует

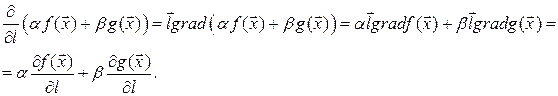
Конец доказательства.

Теорема 15.2. Градиент дифференцируемой функции 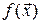в точке 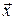указывает на направление наискорейшего возрастания функции 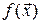в точке .

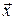Доказательство. Действительно, производная по направлению указывает на скорость возрастания функции в указанном направлении. Так как ( 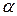‑ угол между векторами)

,

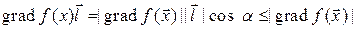то производная по направлению будет максимальна, если 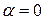, то есть если вектор 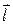будет параллелен градиенту.

Конец доказательства.

Пример 15.1. Вычислить производную по направлению вектора 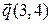от функции 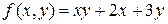и градиент в точке M(1,3).

.

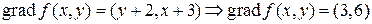Вектор 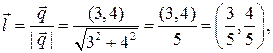тогда

.

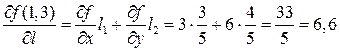Конец примера.

Замечание 15.1. В некоторых случаях удобно пользоваться такими понятиями как направляющие косинусы. Под этим понимают косинус угла между направляющим вектором и соответствующей осью координат. Если 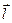‑ единичный вектор, то направляющие косинусы определяются из соотношения

,

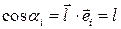где 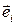‑ орт декартовой системы.

Теорема 15.2. Градиент функции перпендикулярен линии или поверхности равного уровня.

Доказательство. Ограничимся функциями 2-х переменных и докажем, что градиент перпендикулярен линии постоянного уровня, то есть в любой точке линии постоянного уровня градиент перпендикулярен касательной, проведенной к этой точке. Для функции 2-х переменных можно показать, что уравнение касательной к линии 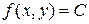в точке 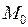равно:

.

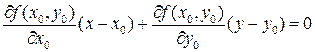Откуда следует, что градиент функции 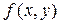перпендикулярен вектору 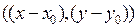, то есть самой касательной.

Определение 15.5. Нормалью к графику функции 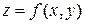в точке 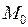называется прямая перпендикулярная любой касательной в этой точке плоскости. Так как уравнение касательной в точке 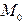плоскости имеет вид

,

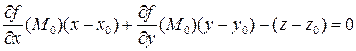то вектор с координатами 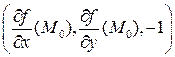будет параллелен нормали в точке 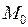, следовательно, уравнение нормали

.

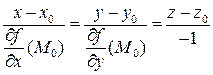Пример 15.2. Для функции 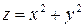вычислить в точке 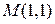уравнение касательной плоскости и нормали.

,

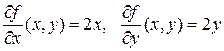тогда получаем:

уравнение касательной плоскости

,

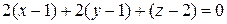уравнение нормали

.

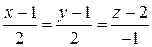Конец примера.