Решение

№70.

Заряд распределен в пространстве по периодическому закону 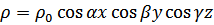, образуя бесконечную пространственную периодическую решетку. Найти потенциал 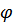электрического поля.

Решение.

Запишем уравнение Пуассона:

.

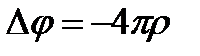Распишем оператор Лапласа и подставим вместо 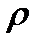заданное распределение заряда:

.

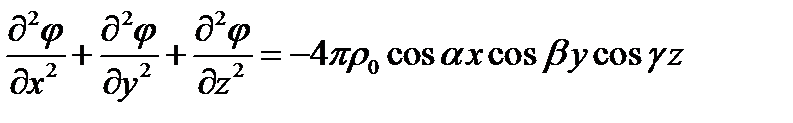Решение будем искать в виде: 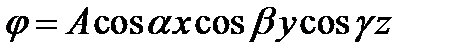(1)

.

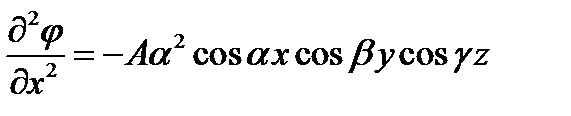
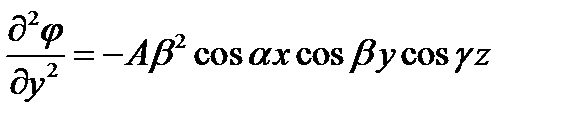
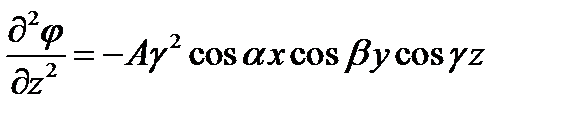
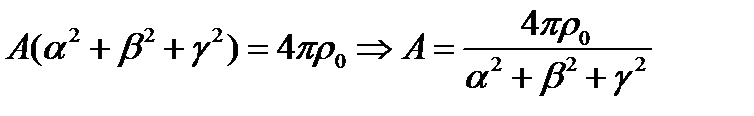Подставим найденную константу 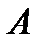в уравнение (1):

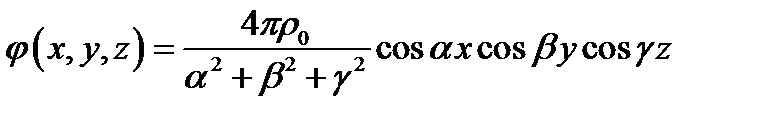
Ответ: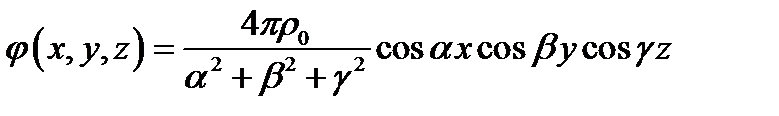

№244.

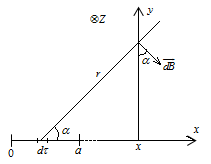
Прямолинейная бесконечно длинная полоса имеет ширину a. Вдоль полосы течет ток J, равномерно распределённый по её ширине. Найти магнитное поле H. Проверить результат, рассмотрев предельный случай поля на больших расстояниях.

Решение.

Рассмотрим для начала бесконечный провод с током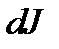

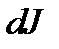Теорема о циркуляции вектора 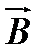: 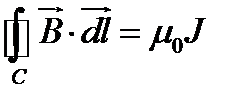. В силу симметрии задач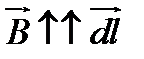и, и 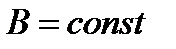, тогда получим выражение: 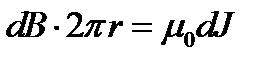откуда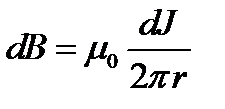

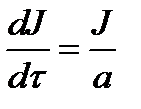
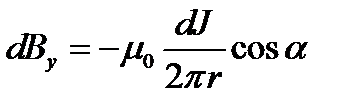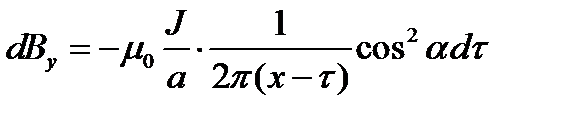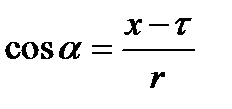; т.к. , то

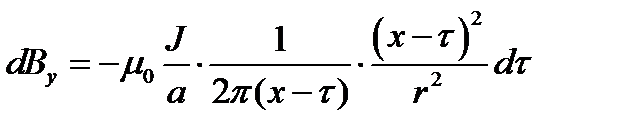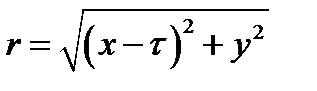. , откуда получаем:

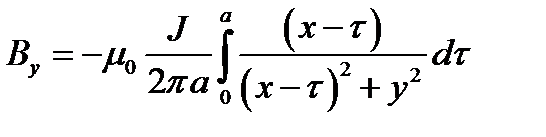
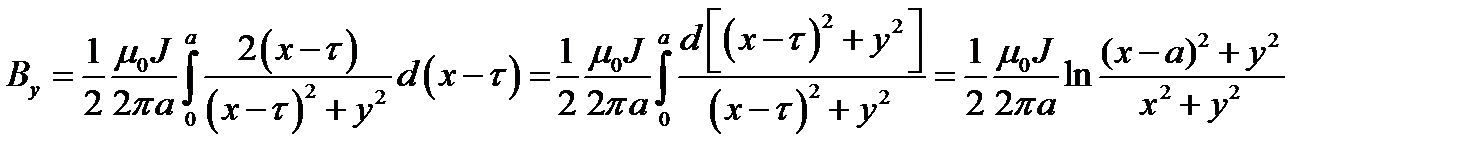
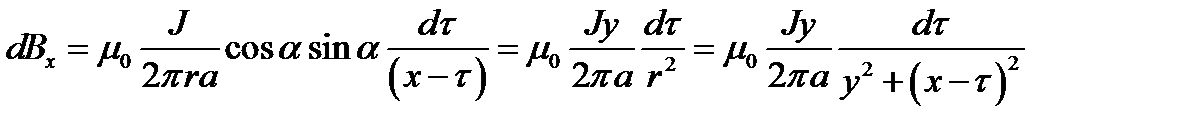
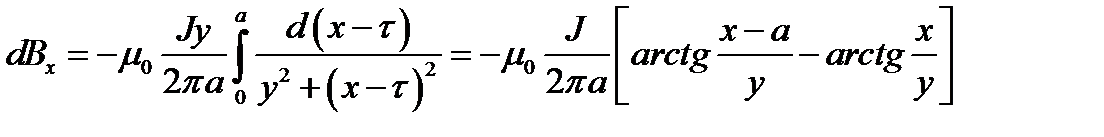
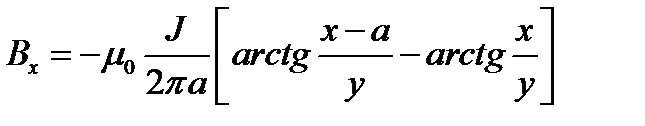
Ответ:

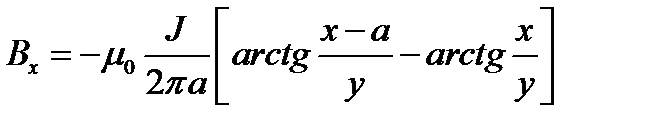
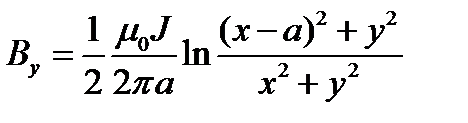
№565.

Релятивистская частица совершает «равноускоренное» одномерное движение (ускорение 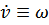постоянно в собственной системе отчета). Найти зависимость скорости 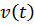и координаты 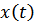частицы от времени t в лабораторной системе отcчета, если начальная скорость 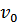, а начальная координата 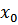. Рассмотреть, в частности, нерелятивистский и ультрарелятивистский пределы.

Указание. Использовать результат предыдущей задачи.