Давление жидкости на плоскую стенку

Рассматривая задачи определения равнодействующей гидростатического давления на плоскую стенку необходимо добиться уяснения студентами следующих положений:

- равнодействующая гидростатического давления – равнодействующая распределенной системы параллельных сил, направленных в одну сторону;

- равнодействующая, как величина векторная характеризуется направлением, модулем и точкой приложения;

- в любом случае для определения модуля равнодействующей необходимо знать площадь плоской стенки 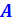и гидростатическое давление в точке, совпадающей с геометрическим центром 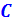площади;

- точка стенки 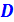, через которую проходит линия действия равнодействующей гидростатического давления называется центром давления; геометрический центр стенки 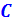не, как правило не совпадает с центром давления .

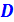3.1. Сила давления жидкости на плоскую стенку

Рассмотрим жидкость, покоящуюся в резервуаре с плоскими стенками, на свободную поверхность которой действует давление 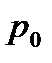(рис.3.1). На правой боковой стенке выделим площадь 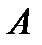, равнодействующую сил давления на которой и определим.

Система декартовых прямоугольных координат имеет оси y,z в плоскости правой стенки; ось x перпендикулярна им. Часть стенки площадью А показана в проекции на плоскость yz. Начало координат находится на линии уреза воды.

Рис. 3.1

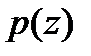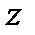
На площадке dA давление не изменяется и определяется величиной глубины погружения . (3.1) Равнодействующая сил давления на площади А стенки определяется интегралом . (3.2)

После интегрирования приходим к формуле

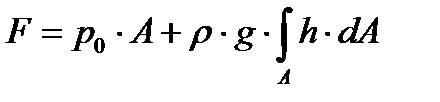(3.3)

Очевидно, что 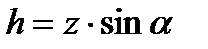, тогда из (3.3) следует

,

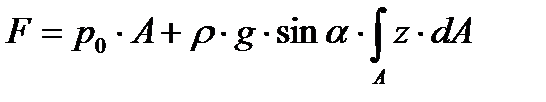(3.4)

Где 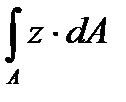- это статический момент рассматриваемой площади стенки относительно оси 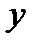. Это обстоятельство позволяет записать формулу (3.4) в следующем виде

,

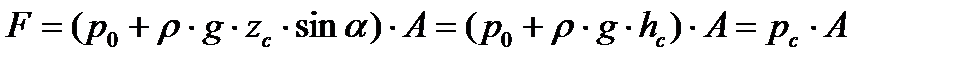(3.5)

где

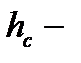· глубина погружения центра площади А;

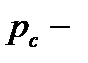· абсолютное давление в точке, совпадающей с центром площади А.

Однако, точка приложения равнодействующей сил давления F – центр давления D, не совпадает с центром площади А ,– точкой .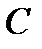

Координата 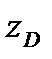центра давления D определяется по формуле

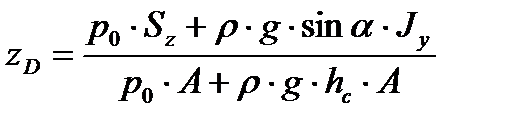(3.6)

Если пренебречь величиной давления на свободной поверхности и считать 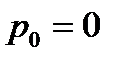, то

.

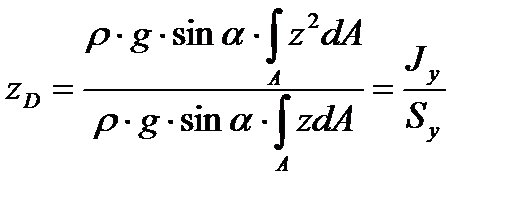(3.7)

Если пьезометрическая составляющая давления существенно ниже давления 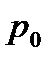, то

.

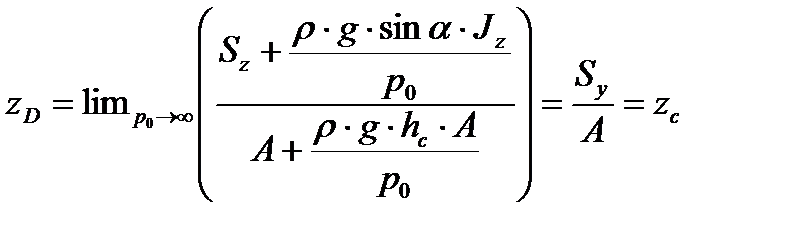(3.8)

В гидравлических расчетах при 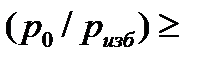10 можно с высокой точностью считать, что центр давления (точка D) совпадает с центром площади А – точкой С.

В том случае, когда ось 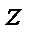не является осью симметрии, необходимо искать и вторую координату центра давления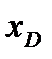

Примеры решения частных задач приведены в таблице 3.1

Табл.3.1

№ п/п	Схема

Примеры решения задач

Пример 3.1

Подпорная прямоугольная вертикальная стенка шириной b = 200 м сдерживает напор воды высотой Н =10 м

Определить силу полного давления на стенку Р и опрокидывающий момент M . Построить эпюру давлений.

Рис. 3.1

Решение

Сила полного давления на стенку определяется по формуле

,

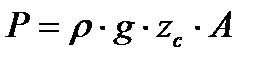(3.9)

где zc − глубина погружения центра тяжести стенки;

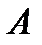− площадь стенки.

Для заданных условий задачи

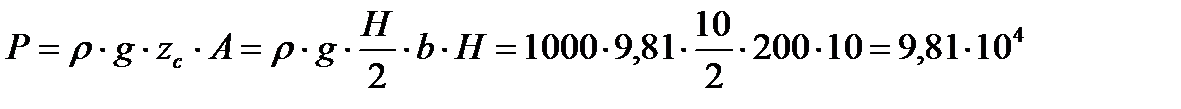кН.

(3.10)

Для определения опрокидывающего момента необходимо знать координату точки приложения силы полного давления, которую можно определить по формуле (3.7)

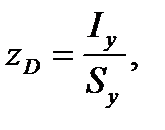(3.11)

где 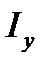− момент инерции площади стенки относительно горизонтальной оси, проходящей в плоскости свободной поверхности жидкости.

Для прямоугольного сечения

.

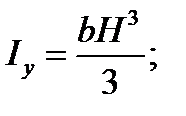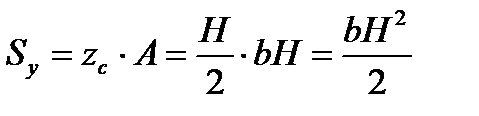(3.11)

Следовательно

.

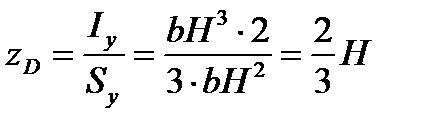(3.12)

Опрокидывающий момент, момент относительно горизонтального ребра, проходящего через точку 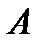, равен

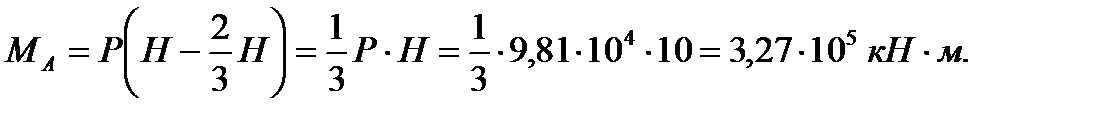(3.13)

Избыточное гидростатическое давление в точке А

,

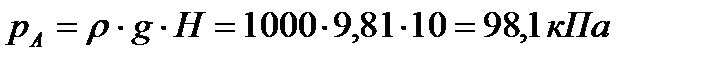(3.14)

а в точке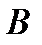

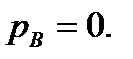
Для построения эпюры избыточного гидростатического давления необходимо в точке А нормально подпорной стенке отложить в масштабе значение 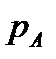, а в точке 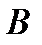принять нулевое значение.

Соединив прямой линией точку В с концом вектора 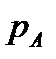, получим эпюру распределения избыточного гидростатического давления по высоте подпорной стенки.

Эпюру абсолютного давления можно построить аналогично, если увеличить избыточные давления в точках А и В на величину .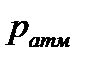

Пример 3.2

Определить силу P полного давления на торцевую, плоскую стенку горизонтальной цилиндрической цистерны диаметром 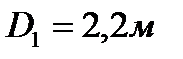и точку ее приложения D, если уровень бензина, плотность которого 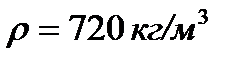,находится на расстоянии Н = 2,4 м от дна цистерны. Цистерна герметически закрыта, избыточное давление паров бензина на свободную поверхность составляет .

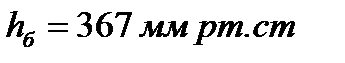Рис. 3.2

Решение

Сила полного давления P на плоскую торцевую стенку цилиндрической цистерны складывается из силы, создаваемой давлением столба бензина высотой

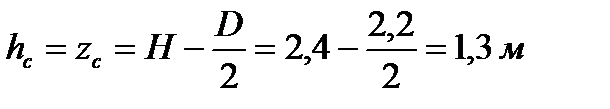(3.15)

и силы, создаваемой избыточным давлением паров бензина 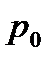, соответствующего hб

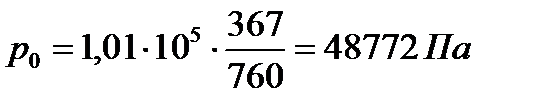(3.16)

Так как 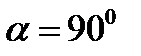(см. рис. 3.1), получаем

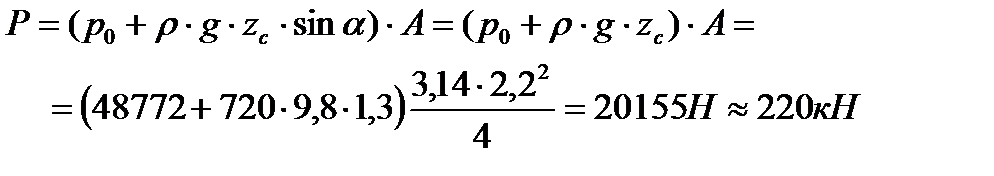(3.17)

Для плоской стенки расстояние точки приложения силы полного давления от свободной поверхности жидкости равно

,

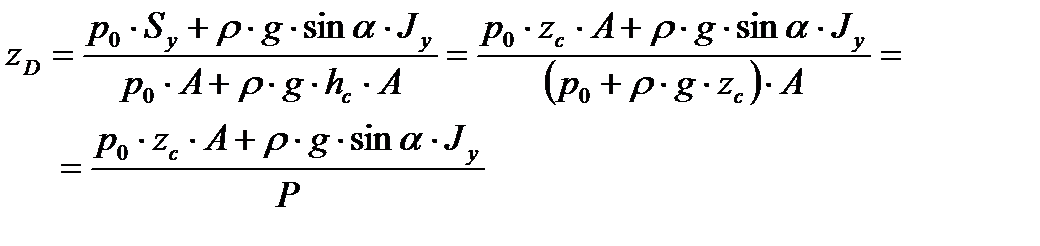(3.18)

где 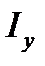− момент инерции площади смоченной поверхности стенки относительно горизонтальной оси 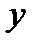, проходящей по краю свободной поверхности жидкости.

Т.к. плоская стенка имеет форму круга

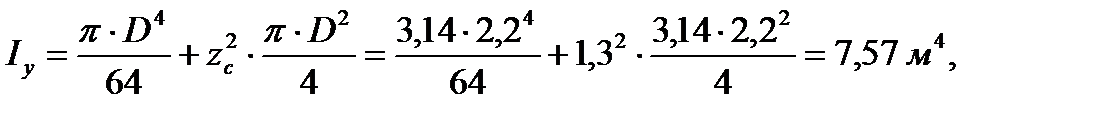(3.19)

После подстановки численных значений в формулу ( ) находим

,

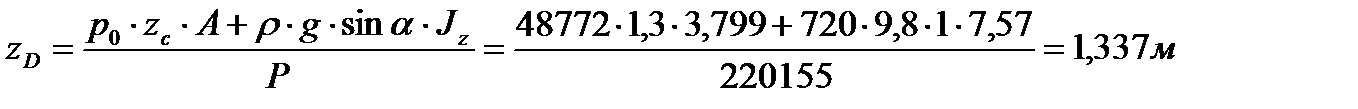(3.20)

Пример 3.3

Трубопровод диаметром d = 0,7 м перекрыт круглым дроссельным затвором, вращающимся на горизонтальной оси. Слева от затвора трубопровод заполнен водой под манометрическим давлением 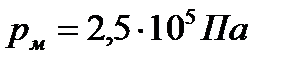. Момент какой величины нужно приложить к оси затвора, чтобы он не открывался под действием давления воды?

Рис.3.3

Решение

Манометрическое давление распределяется по площади затвора равномерно. Его результирующая проходит через ось затвора и, следовательно, момента не дает.

Момент создает сила давления находящейся в трубопроводе воды, приложенная в центре давления затвора на глубине .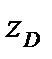

Сила давления воды на затвор определяется по формуле

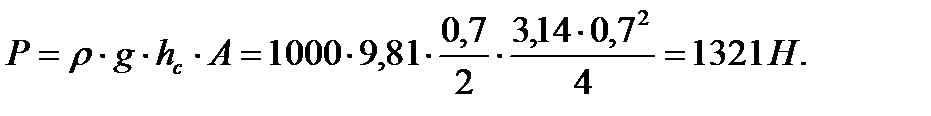(3.21)

Координата центра давления 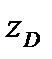определяется по формуле (3.7)

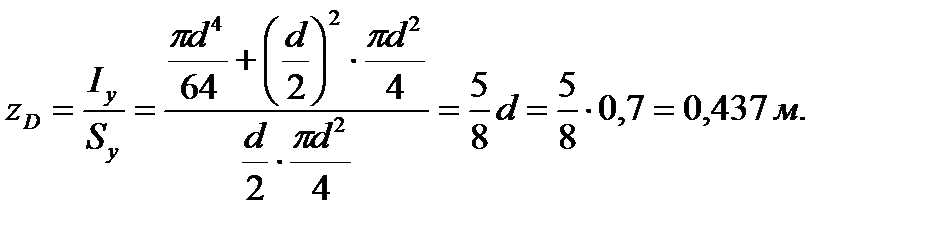(3.22)

К оси затвора необходимо приложить момент, равный произведению силы Р на расстояние 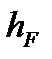между центром давления и центром тяжести затвора, расположенным на оси трубы

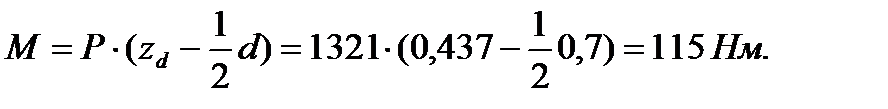(3.23)

Пример 3.4

В резервуар налит керосин с плотностью 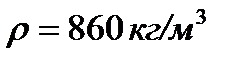. Требуется определить диаметры d болтов, прикрепляющих крышку лаза, и найти положение центра давления на крышку, если уровень керосина в резервуаре находится на расстоянии H = 8 м от дна, число болтов п =12 , диаметр лаза d = 0,75 м и расстояние от его центра тяжести до дна h = 1 м . Допускаемое напряжение на разрыв для болтов .

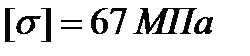Рис. 3.4

Решение

Свободная поверхность жидкости в резервуаре находится под воздействием атмосферного давления. Действие атмосферного давления передается на внутреннюю поверхность крышки лаза, но оно же действует и на наружную поверхность крышки. Следовательно, расчет на прочность болтов, прикрепляющих крышку к фланцу лаза, должен выполняться только с учетом давления, создаваемого давлением столба жидкости.

Давление на крышку меняется по линейному закону от величины 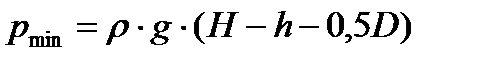до максимального значения 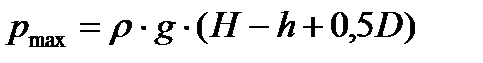. График изменения 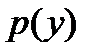представлен на рис. 3.4.

Определяем равнодействующую гидростатического давления на крышку лаза

.

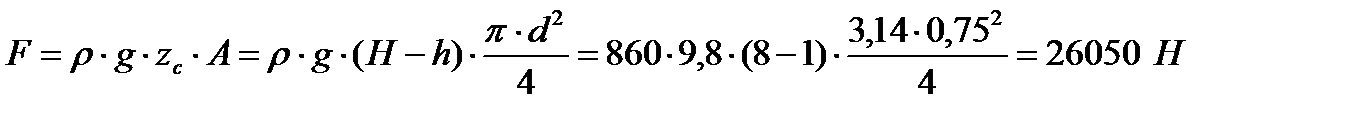(3.24)

Сила 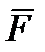приложена в точке 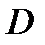крышки, координата которой определяется по формуле (3.7)

.

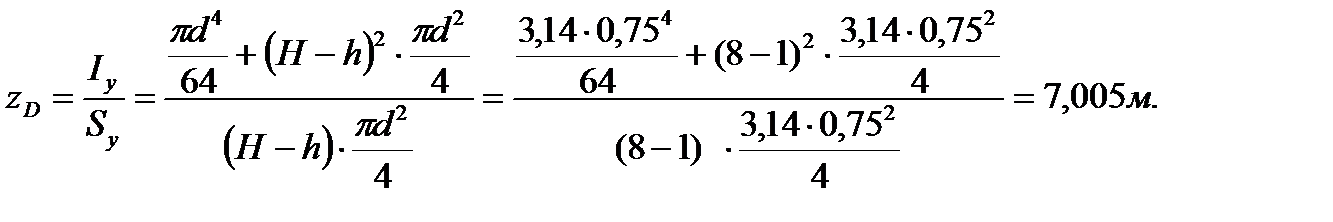(3.25)

Смещение линии действия силы 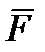относительно оси крышки невелико, всего 5 мм, поэтому будем рассчитывать болты, считая, что нагрузка между болтами распределяется равномерно. Диаметр тела болта найдем из условия прочности при растяжении

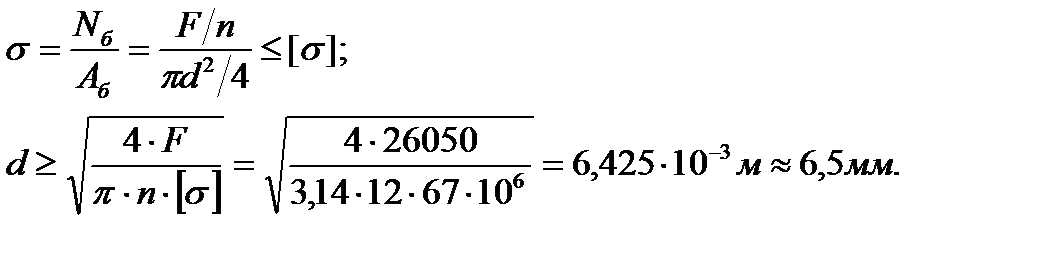(3.26)

Для крепления крышки необходимо выбрать болт стандартного диаметра .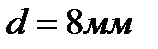

Пример 3.5

Построить эпюру гидростатического давления на ломаную стенку заполненного водой резервуара.

Определить силы полных давлений и точки их приложения на участке ломаной стенки АВС длиной L = 1м, , .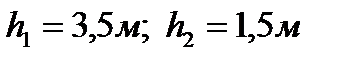

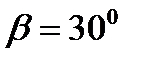Рис. 3.5

Решение

Для построения эпюры избыточного гидростатического давления необходимо рассчитать величину значения давлений в точках 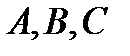. Величина избыточного гидростатического давления определяется глубиной погружения точки от свободной поверхности

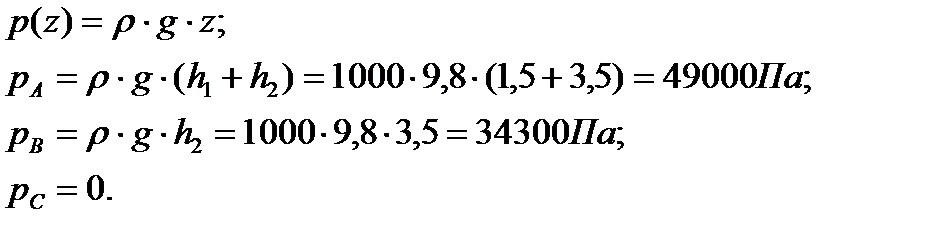(3.27)

Вектор давления проводим перпендикулярно поверхности стенки на каждом участке. Ординаты откладываем в масштабе (рис. 3.5).

Для определения результирующей гидростатического давления на каждом участке стенки необходимо найти давление в центре этого участка стенки:

На участке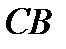

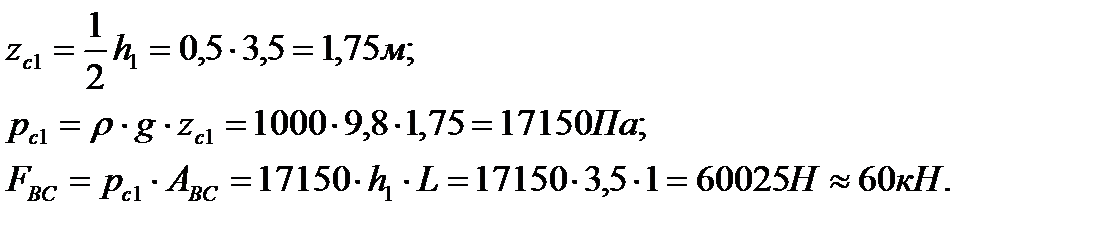(28)

На участке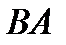

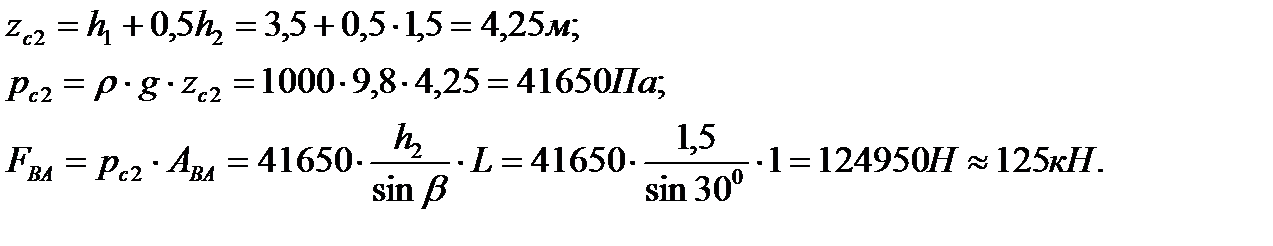(3.29)

При определении координат 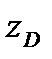, точек приложения равнодействующих сил гидростатического давления на поверхностях 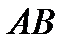и 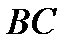необходимо учесть, что в формуле (3.6) для поверхности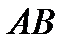 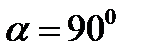, а для поверхности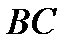 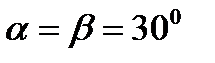. Для поверхности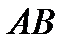 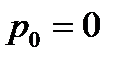, а для поверхности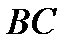 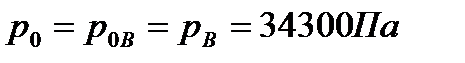. Тогда имеем

для поверхности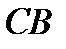

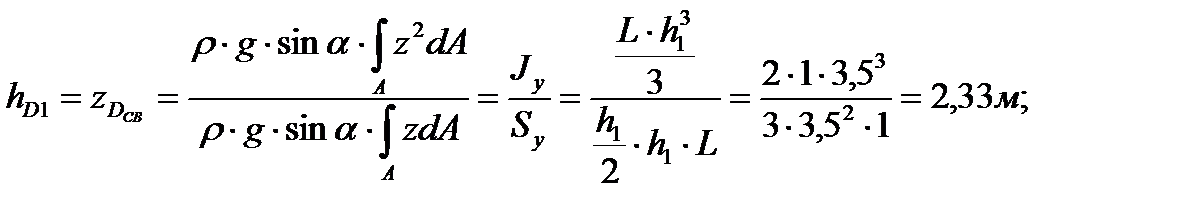(3.30)

для поверхности 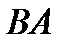(3.5 б))

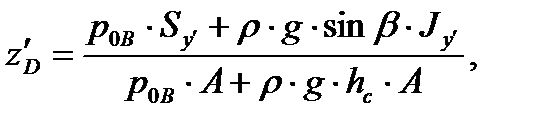(3.31)

где:

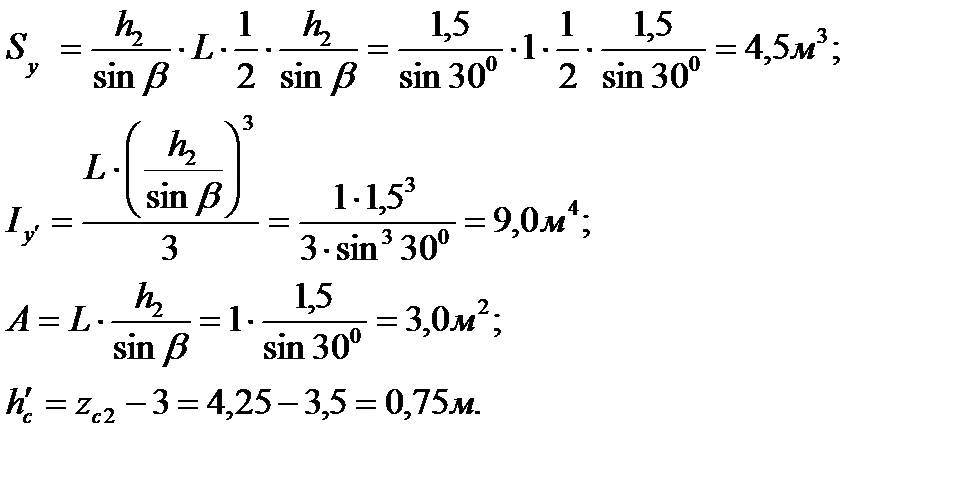
Тогда

.

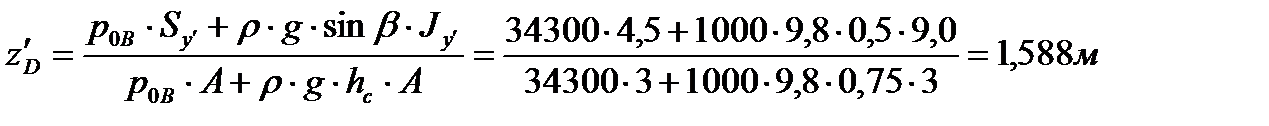(3.32)

Центр давления поверхности 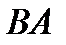располагается от свободной поверхности жидкости на глубине

.

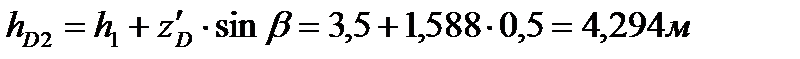(3.33)

Центр давления поверхности 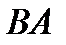располагается ниже ее центра тяжести по вертикали на расстояние .

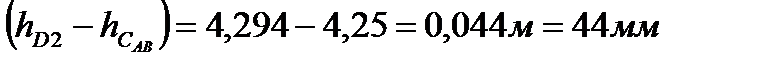Пример 3.6

Щит, перекрывающий канал, расположен под углом 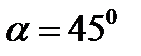к горизонту и закреплен шарнирно к опоре над водой (рис.3.6).

Определить усилие T, которое необходимо приложить к тросу для подъема щита, если ширина щита b = 2 м, глубина воды перед щитом h1 = 2,5 м, а после щита h2 =1,5м. Шарнир расположен над высоким уровнем воды на расстоянии h3 = 1м. Весом щита и трением в шарнирах можно пренебречь.

Рис. 3.6

Решение

Для определения минимального значения силы 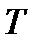, необходимой для поворота щита, необходимо рассмотреть равновесие щита 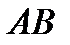под действием приложенных к нему сил 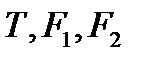, (см. рис. 3.6). Весом щита и силами трения пренебрегаем.

Сила полного давления воды на щит с левой стороны

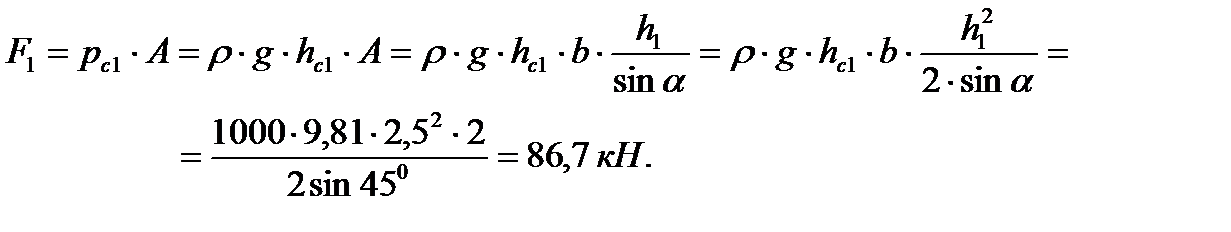(3.34)

Сила полного давления воды на щит с правой стороны определяется аналогично

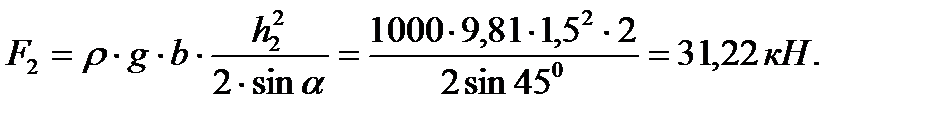(3.35)

Определим расстояния от шарнира 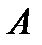до центров приложения сил давления (точки 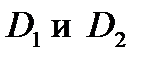). Расчет проводим, учитывая только гидростатическое давление. Используем формулу (3.7).

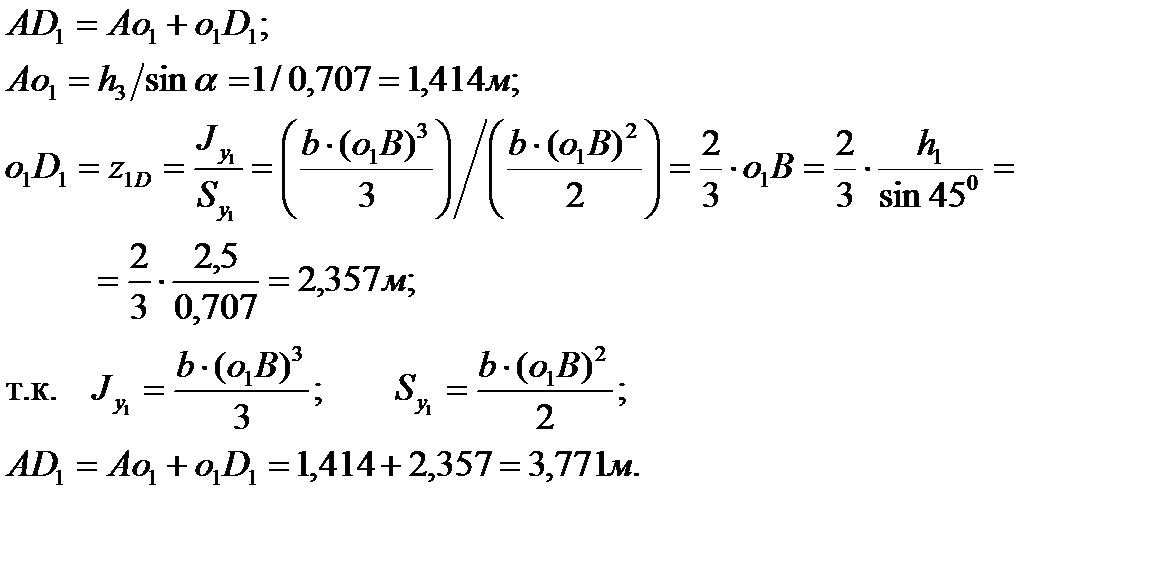(3.36)

Расстояние от точки приложения силы P2 до шарнира определяется аналогично

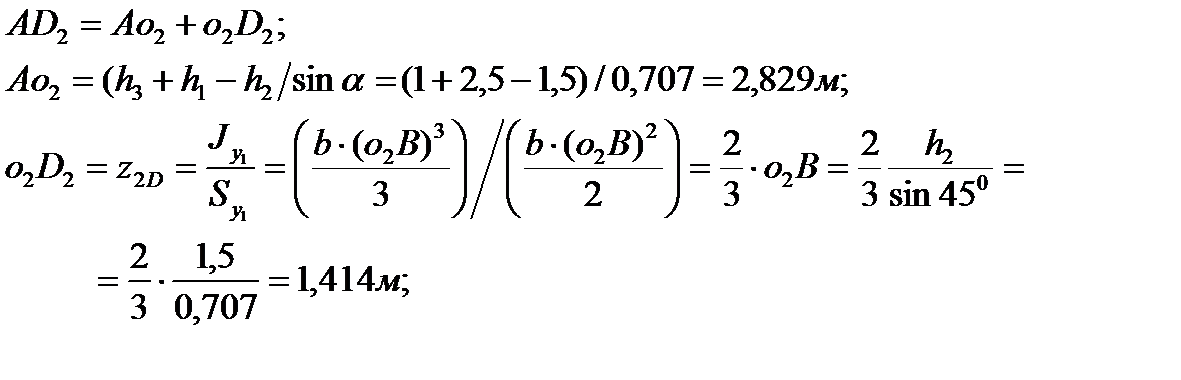	(3.37)
,

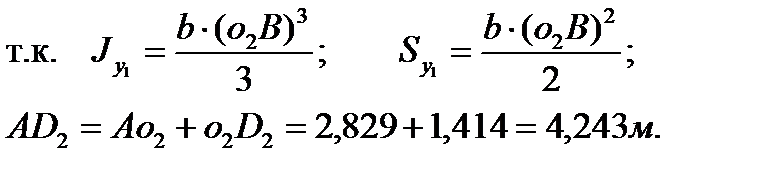Чтобы определить усилие Т, необходимое для подъема щита, составим уравнение моментов всех сил относительно шарнира

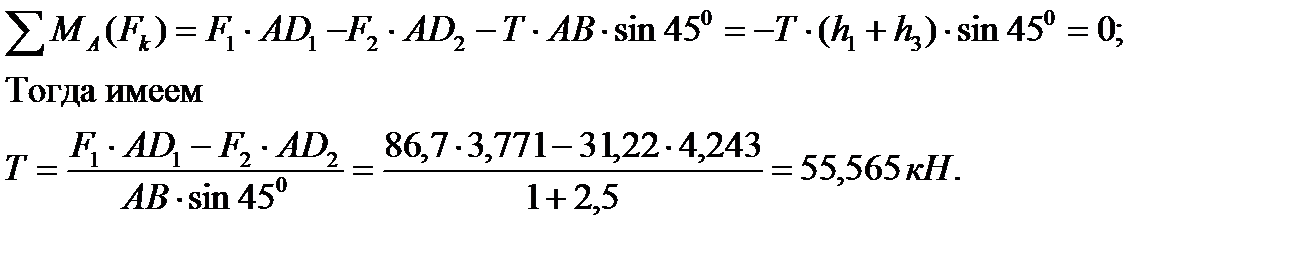(3.38)
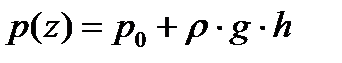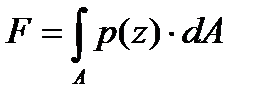