Арапайым дифференциалдыҚ теҢдеулер. коши есебініҢ шешу Әдістері

6.1 Коши есебі

Коши есебі: қарапайым дифференциалдық теңдеуге қатысты негізгі есеп бастапқы шартты (1) қанағаттандыратын u=u(t) түріндегі шешімін табу -Коши есебі.

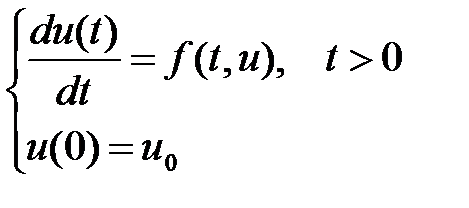(1)

(1) есептің оң жағындағы 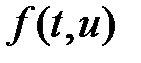функция белгілі шарттарды қанағаттандырса (қанағатандырады деп санаймыз) онда Коши есебінің шешімі бар және сол шешімі жалғыз.

айнымалының өзгеру аралығында тұрақты қадамы бар тор енгіземіз, яғни 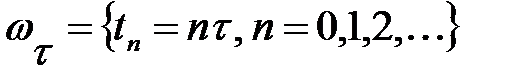нүктелер жиынын қарастырамыз.

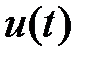белгісіз функцияның 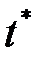нүктедегі мәнін табу керек. Ол үшін 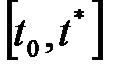аралықты 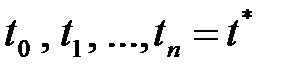түйындермен 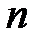аралыққа бөлеміз.

Жуықтап табу формулалары қолданылып 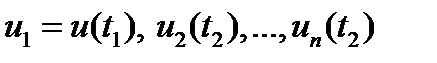функция мәндері табылады.

Жуықтап табу 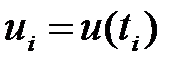формулаларының көбi келесі принциппен табылады. (1) теңдеуді дифференциал түрінде жазып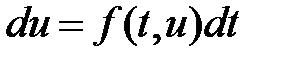 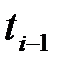және 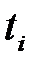аралығында интегралдасақ:

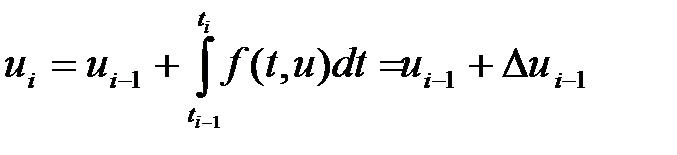. (2)

Көптеген әдістердің негізінде осы формула жатыр. Әдістердің бір бірінен айырмашылығы функция өсімшесін (3) табу әдісіне байланысты.

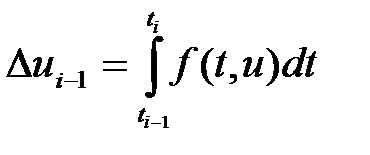. (3)

6.2 Эйлера әдісі, қайта есептеу Эйлер (Эйлер-Коши) әдісі

Эйлер әдісінде функция өсімшесін тапқанда интеграл солжақты ушбұрыш формуласыменен табылады:

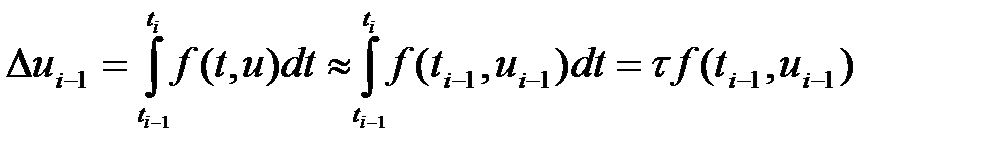, (4)

(2) теңдеу келесі түрде жазылады:

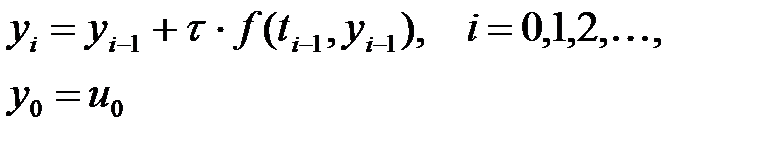. (5)

бір қадам аралығында (4), (5) формулалар қателігі:

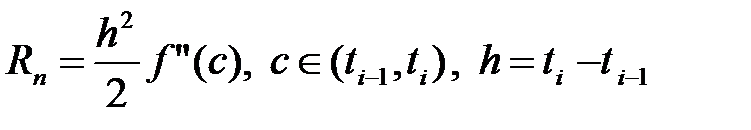. (6)

Бір қадам аралығында әдіс қателігі 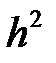-ретті.

Қайта есептеу Эйлер (Эйлер-Коши) әдісінің негізгі идеясы келесіде: біріншіден Эйлер формуласыменен нөлдік жұықтау табылады:

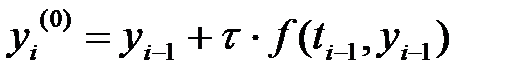. (7)

Одан кейін 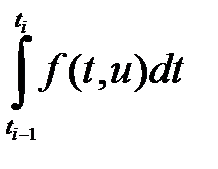интеграл трапеция формусамын есептеледі. Яғни, 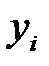жуықтап табу формуласы келесі түрде табылады:

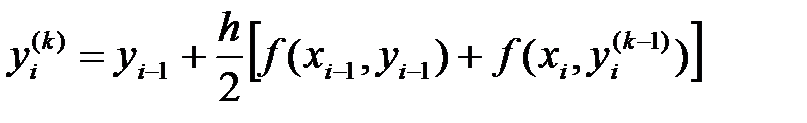. (7*)

(7*) формуланың көмегімен функция мәнінің 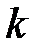нөмерлі итерациялық мәні табылады. Итерация 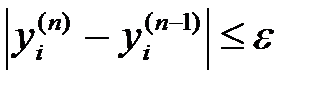, 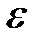-кішкентай сан, шарт орындалғанша есептеледі.

Бір қадам аралығында әдіс қателігі 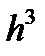-ретті.

Мысал 1

Есептгегенде 3-дұрыс цифрлар қолдана отырып Коши есебін Эйлер әдісімен шеш, h=0,125:

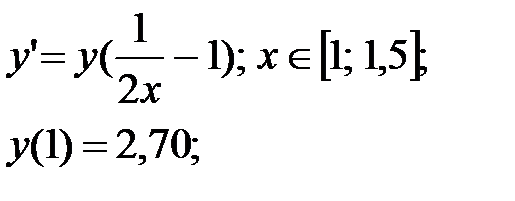
Шешім:

Берілгеніне сәйкес x₀=1, y₀=2,70.

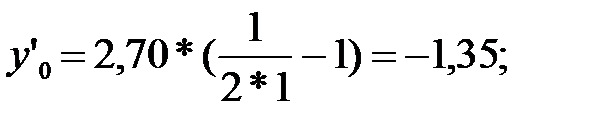
(4) формула, .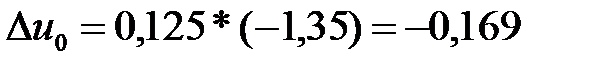

Сонымен (5) формула бойынша y₁=2,70-0,169=2,53.

Арғарай итерация жалғаса береді. Бастапқы мән ретінде x₁, y₁, келесі итерацияда x₂, y₂ және т.б. алынады. Есептеу нәтижесі 1-кестеде келтірілген.

1-кесте. Эйлер әдісімен есептеу

i	xi	yi	y'i	∆yi
	1,000	2,70	-1,35	-0,169
	1,125	2,53	-1,41	-0,176
	1,250	2,36	-1,41	-0,176
	1,375	2,18	-1,38	-0,172
	1,500	2,01

Мысал 2

Есептгегенде 3-дұрыс цифрлар қолдана отырып Коши есебін Эйлер-Коши әдісімен шеш:

; ;

;

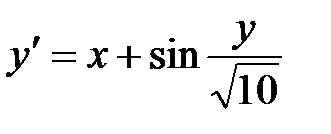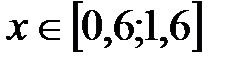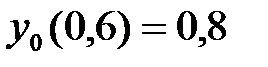Шешім:

Эйлер формуласымен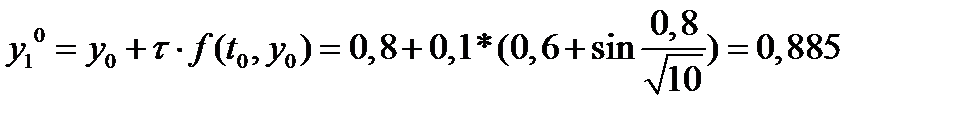

табамыз.

Нөлдік жуықтау табылды, енді 1-інші жуықтауды (итерацияны) табамыз:

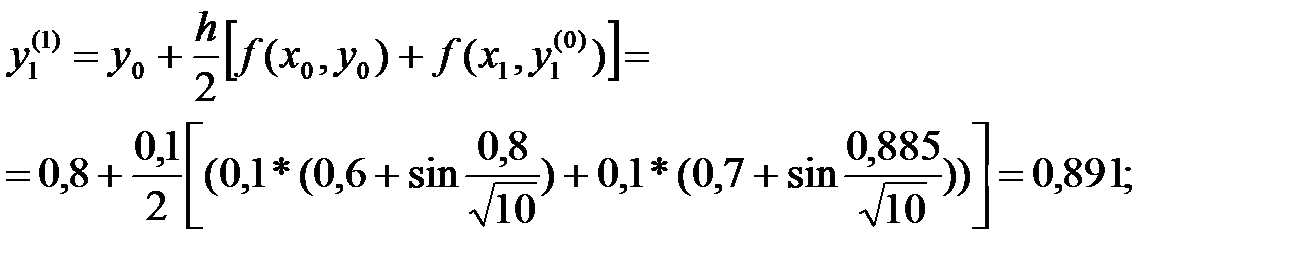
Екінші итерация:

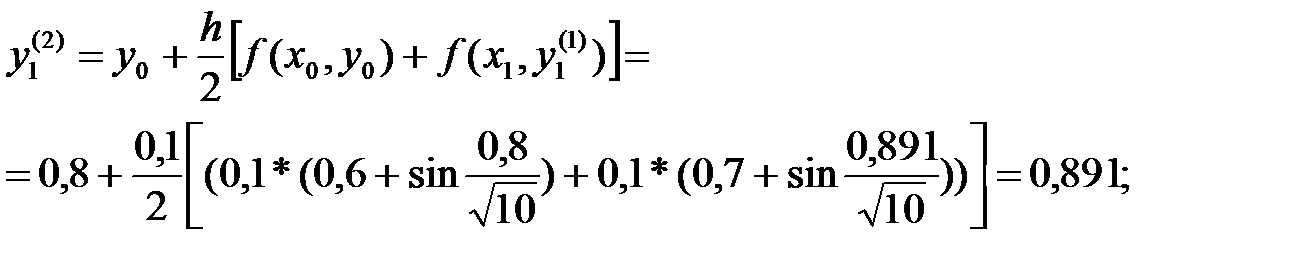
Бірінші және екінші итерациялардың нәтижесі бір біріне сәйкес, сондықтан есептеу тоқтатылады. Табылған y₁=0,891.

Осылай қалған y_{i ,} i=2…10, анықталады.

Есептеу нәтижесі 2-кестеде келтірілген.

2-кесте. Эйлер-Коши әдісімен есептеу

i	Xi	Yi	Итерация ( k )
	0,6	0,8	-	-	-	-
	0,7	0,891	0,885	0,891	0,891
	0,8	0,996	0,989	0,996	0,996
	0,9	1,114	1,107	1,113	1,114	1,114
		1,245	1,238	1,245	1,245
	1,1	1,390	1,383	1,390	1,390
	1,2	1,550	1,543	1,550	1,550
	1,3	1,725	1,717	1,725	1,725
	1,4	1,914	1,907	1,914	1,914
	1,5	2,119	2,111	2,119	2,119
	1,6	2,338	2,331	2,338	2,338

6.3 Рунге-Кутта әдісі

Айқындалған m-қадамды Рунге-Кутта әдісі келесіден тұрады. Коши есебінің шешімі белгілі деп санайық. Сандық коэффициенттер анықталады және ретімен функциялар есептеледі:

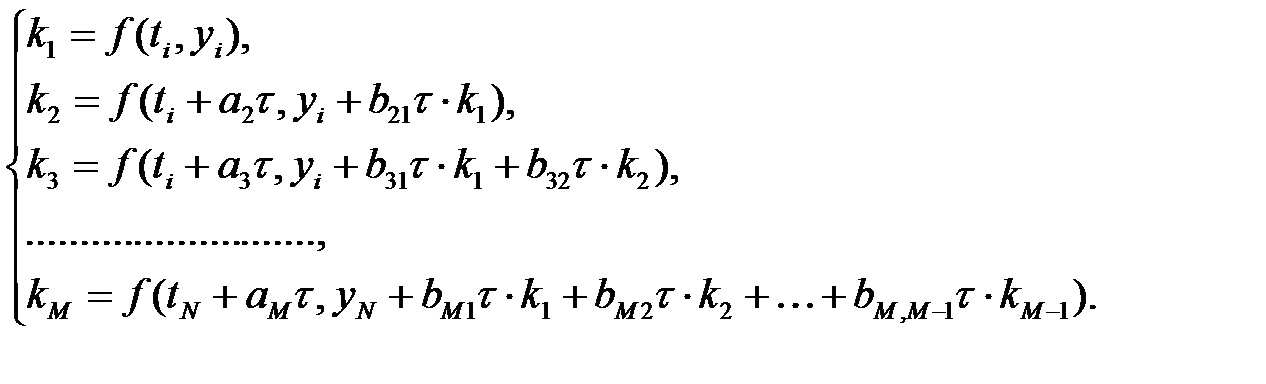(8)

Одан кейін, келесі формуламен:

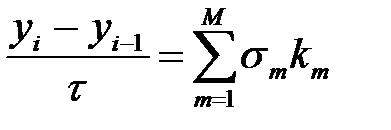(9)

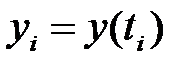жаңа мәні есептеледі.

Төртқадамды Рунге-Кутта әдісінде алдымен келесі элементтер есептеледі:

,

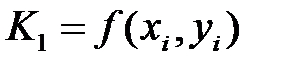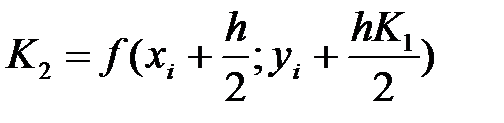, (10)

,

,

.

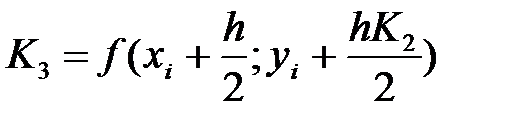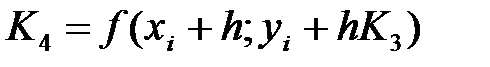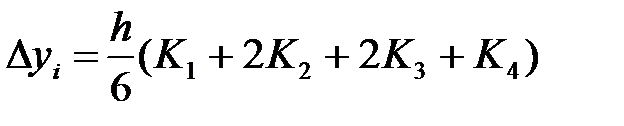Одан кейін, келесі формуламен Коши есебінің жұықталған шешімі есептеледі:

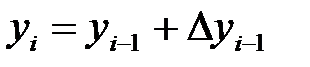. (11)

Бір қадам аралығында әдіс қателігі h⁵ – ретті.

Мысал 3

Есептегенде 3-дұрыс цифрлар қолдана отырып Рунге-Кутта әдісімен Коши есебін шеш, h=0,5:

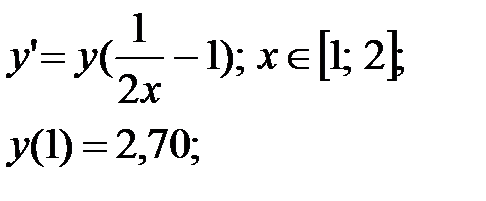
Шешім: Алдымен i=0, K₁, K₂, K₃, K₄ элементтерді есептейміз:

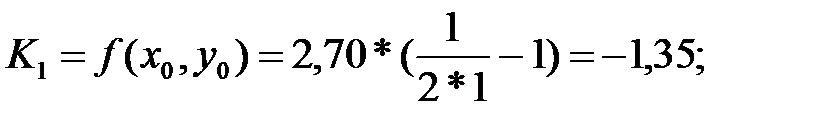
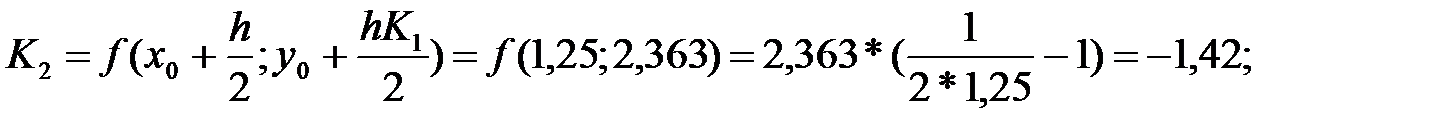
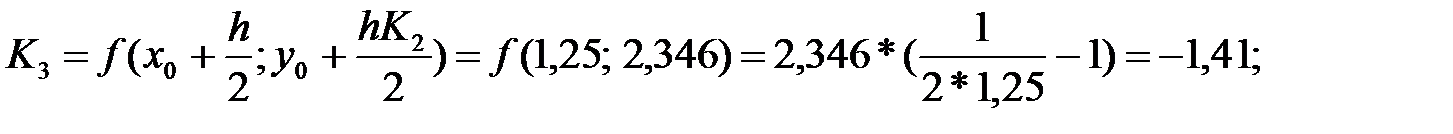
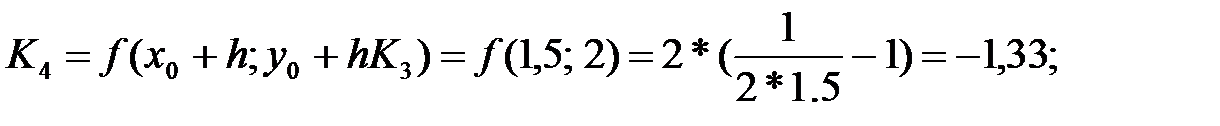
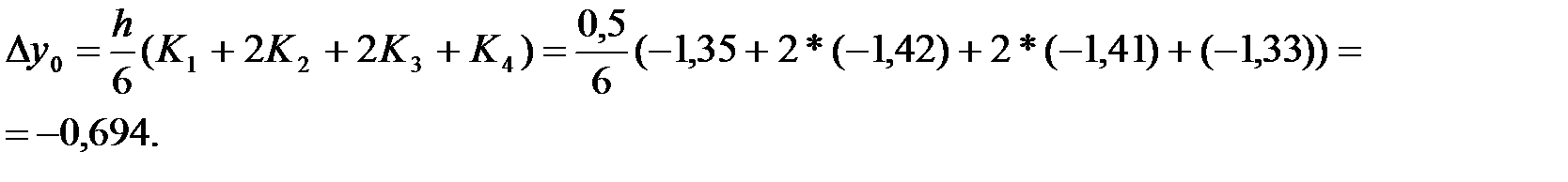
x=1,5 түйінде: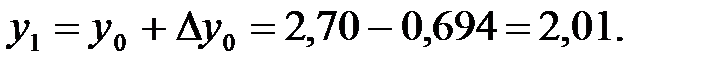

Басқа түйіндерде функция мәні жоғарыда жазылған ретімен табылады. Әдісті қолдану нәтижесі 3-кестеде келтірілген:

3 -кесте. Рунге-Кутта әдісін жүзеге асыру.

i	xi	yi	K1	K2	K3	K4	∆xi
	1,00	2,70	-1,35	-1,42	-1,41	-1,33	-0,694
	1,50	2,01	-1,34	-1,19	-1,22	-1,05	-0,601
	2,00	1,40	-1,05	-0,888	-0,920	-0,756	-0,452
	2,50	0,953	-0,762	-0,624	-0,652	-0,522	-0,320
	3,00	0,633	-	-	-	-	-

7 ҚАРАПАЙЫМ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР