Построение ортонормированного базиса из собственных векторов.

Все определения и свойства линейных преобразований сохраняют свое значение и в евклидовых пространствах. Вместе с тем наличие скалярного произведения позволяет выделить важные частные классы линейных преобразований. К таким классам относятся сопряженные и самосопряженные преобразования.

Линейное преобразование f^* с матрицей L^* называется сопряженнымданному преобразованию f с матрицей L, если для любых векторов 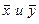из R_n имеем

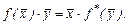т.е.

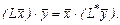
Выясним, как связаны матрицы L и L^*в некотором ортонормированном базисе .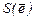

По определению сопряженного преобразования для любых векторов 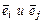ортонормированного базиса 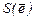верно равенство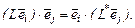

Образы базисных векторов имеют вид 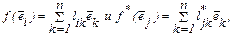а тогда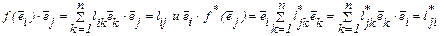

В итоге 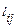= 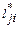при любых i и j и, следовательно, матрица сопряженного преобразования получается из матрицы L транспонированием: L^* = L^T.

Заметим, что если L – ортогональная матрица, т.е. L^T = L^-1, то сопряженное преобразование есть обратное преобразование: L^* = L^-1.

Линейное преобразование f называется самосопряженным, если для любых векторов 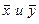из R_n верно равенство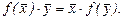

Другими словами, линейное преобразование самосопряженно, если оно совпадает со своим сопряженным, т.е. L = L^T. В этом случае матрица L симметрическая.

Перечислим основные свойства самосопряженных преобразований.

1⁰. Все собственные значения самосопряженного преобразования действительны.

Например, для n = 2 характеристическое уравнение имеет вид 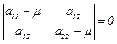или 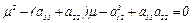. Дискриминант квадратного трехчлена 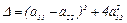неотрицателен и корни трехчлена действительные.

2⁰. Собственные векторы самосопряженного преобразования, принадлежащие различным собственным значениям, ортогональны.

Действительно, пусть 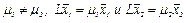, тогда из равенства 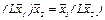следует, что 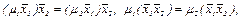что возможно только при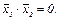

3⁰. В евклидовом пространстве существует ортонормированный базисиз собственныхвекторов самосопряженного линейного преобразования. Данное утверждение называют основной теоремой о самосопряженных преобразованиях. Из него следует, в частности,

Теорема. В базисе из единичных собственных векторов линейного преобразования матрица этого преобразования диагональная, причем элементами главной диагонали являются ее собственные значения.

Действительно, линейное преобразование вполне определено, если заданы образы базисных векторов.

Но если базисными являются единичные векторы 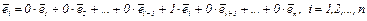, то их образы, принадлежащие собственным значениям 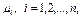имеют вид

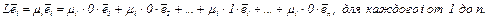
А тогда матрица такого линейного преобразования диагональная: .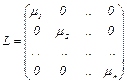

Задача 0.64. Найти собственные значения и собственные векторы самосопряженного преобразования с матрицей 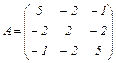. Найти ортонормированный базис из собственных векторов и составить матрицу перехода от исходного базиса к найденному.

Решение. Характеристическое уравнение 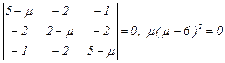имеет корни
μ₁ = 0 , μ₂ = μ₃ = 6. При μ₁ = 0 из системы уравнений 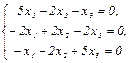находим отношение координат собственного вектора х₁: х₂: х₃ = 1: 2: 1 и тогда 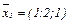- первый собственный вектор. При μ₂ = μ₃ = 6 система уравнений 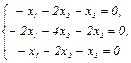сводится к одному уравнению х₁ + 2х₂ + х₃ =0, поэтому отношение координат собственного вектора однозначно определить нельзя. Собственному значению μ = 6 соответствует бесчисленное множество неколлинеарных собственных векторов, перпендикулярных вектору 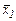. Из этих векторов можно произвольным образом выбрать два ортогональных вектора. Например, в качестве 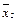возьмем вектор 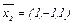, т.к. его координаты удовлетворяют уравнению
х₁ + 2х₂ + х₃ =0. Тогда координаты собственного вектора 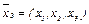, ортогонального векторам 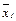и 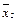, определяются уравнениями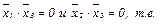 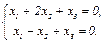. Получаем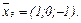

Очевидно, что собственные векторы попарно ортогональны, т.к. 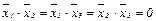. Нормируя их, получим искомый базис: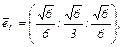

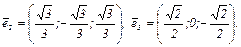
Ответ: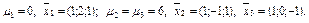

Матрица перехода от исходного базиса к найденному состоит из координатных столбцов нового

ортонормированного базиса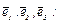

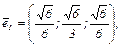
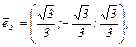
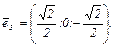
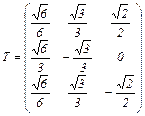
§5. Квадратичная форма, ее матрица и канонический вид.

Пусть в ортонормированном базисе 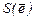симметрическая матрица 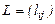n - го порядка определяет самосопряженное линейное преобразование f. Квадратичной формой, связанной с преобразованием f называется функция k( 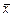), ставящая в соответствие каждому вектору 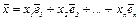некоторое число по формуле: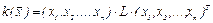

Матрица L называется матрицей квадратичной формы k( 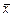) в заданном базисе .

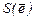Задача 0.65. Записать квадратичную форму, имеющую матрицу А =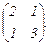

Решение. По определению k( ) =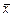

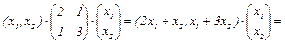
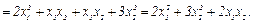Ответ: k( ) = .

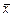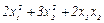Квадратичная форма k( 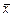) содержит произведения координат вектора 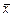и их квадраты, поэтому иногда говорят, что квадратичная форма – это однородный многочленвторой степени от n переменных. Его принято записывать так, что диагональные элементы матрицы L являются коэффициентами при квадратах переменных, а каждый внедиагональный элемент равен половине коэффициента при произведении соответствующих переменных.

Задача 0.66. Квадратичная форма 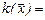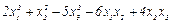имеет матрицу А. Найдите эту матрицу.

Решение. Используя связь между коэффициентами квадратичной формы и элементами матрицы, получаем: 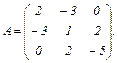Ответ: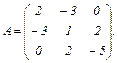

Переход от базиса 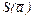к новому базису 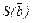влечет за собой и преобразование координат вектора 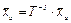и изменение матрицы линейного преобразования L^* = T ^-1 L T. И если базис 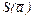ортонормированный, то матрица Т перехода к новому базису ортогональная, т.е. Т^T = Т ^-1, а тогда
L^* = T^T L T. Эта формула определяет закон изменения матрицы квадратичной формы при замене ортонормированного базиса пространства.

Представляет особый интерес новый базис, в котором квадратичная форма принимает наиболее простой (канонический вид).

Теорема. Для каждой квадратичной формы существует ортонормированный базис, в котором она имеет так называемый диагональный вид: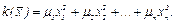

Доказательство. По определению с каждой квадратичной формой связана симметрическая матрица L, которая является матрицей некоторого самосопряженного преобразования.

По основной теореме о самосопряженных преобразованиях в евклидовом пространстве существует ортонормированный базис из собственных векторов матрицы L. В этом базисе матрица L диагональная (см. теорему §4), причем по главной диагонали расположены собственные значения μ₁, μ₂,…, μ_n. Поэтому в указанном базисе квадратичная форма имеет канонический (диагональный) вид: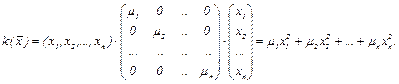

Задача 0.67. Найти базис, в котором квадратичная форма 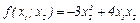имеет диагональный вид.

Решение. Квадратичная форма f с матрицей А= 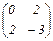имеет диагональный вид в ортонормированном базисе из собственных векторов матрицы А. Характеристическое уравнение 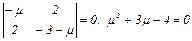имеет корни μ₁ = -4, μ₂ = 1.

Находим и нормируем собственные векторы.

1). μ₁ = -4.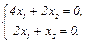

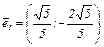
2). μ₂ = -1.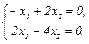

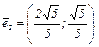
Матрица перехода от старого базиса к базису 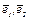имеет вид 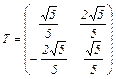, а тогда координаты вектора (х₁, х₂) преобразуются по формулам: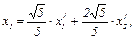

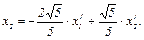
В результате квадратичная форма принимает диагональный вид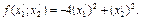

Ответ: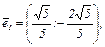

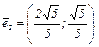
Определение. Число ненулевых коэффициентов в квадратичной форме диагонального вида равно рангу ее матрицы и называется рангом квадратичной формы. Разность между числом положительных и числом отрицательных коэффициентов квадратичной формы диагонального вида называется сигнатурой квадратичной формы и обозначается δ.

Оба названных числа не зависят от базиса, в котором получен диагональный вид квадратичной формы.

Задание №4.

№1. Показать, что векторы 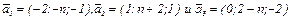образуют базис в трехмерном линейном пространстве и найти разложение вектора 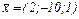по векторам этого базиса. Выполнить проверку.

№2. Первый базис пространства L₃ состоит из векторов 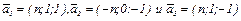. Второй базис состоит из векторов 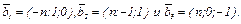Составить формулы, выражающие новые координаты вектора 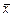через его старые координаты при переходе от первого базиса 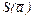ко второму базису .

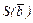№3. Найти собственные значения и принадлежащие им собственные векторы матрицы

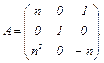
№4. При каком значении 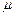базис, образованный векторам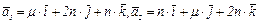и и 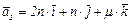является ортогональным? Нормировать этот базис, если базис 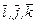- ортонормированный.

№5. Найти ортонормированный базис из собственных векторов матрицы квадратичной формы 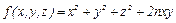и составить формулы преобразования координат х, у и z при переходе к новому базису. Квадратичную форму представить в диагональном виде.