Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы
Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии.
Парные коэффициенты корреляции рассчитываются по формулам:
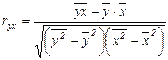 ;
; 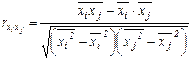 .
.
Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;
2) заполнит диалоговое окно ввода данных и параметров вывода (рисунок 1.3);
3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рисунке 1.4.
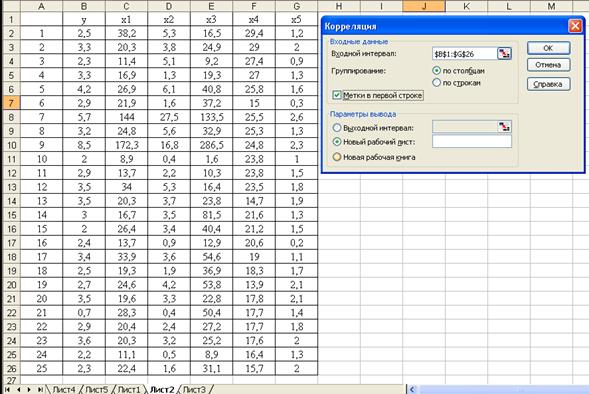
Рисунок 1.3 - Диалоговое окно ввода параметров инструмента Корреляция
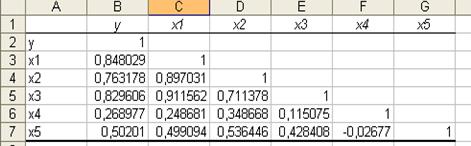
Рисунок 1.4 – Матрица коэффициентов парной корреляции
Из матрицы можно заметить, что факторы 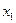 и
и 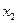 ,
, 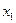 и
и 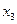 мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,75. Таким образом, можно сказать, что они дублируют друг друга.
мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,75. Таким образом, можно сказать, что они дублируют друг друга.
При отборе факторов в модель предпочтение отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В нашем примере получаем, информативными факторами являются: 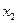 и
и 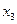 .
.
Построим новое уравнение множественной регрессии с информативными факторами.
Постройте модель в естественной форме только с информативными факторами и оцените ее параметры.
Построим уравнение множественной линейной регрессии следующего вида:
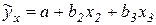 .
.
Параметры вычисляем аналогично пункту 1 (рисунок 1.5).
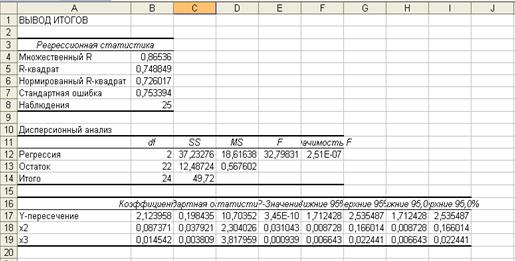
Рисунок 1.5 – Результат применения инструмента Регрессия
Получаем уравнение следующего вида: 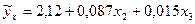 .
.
Выводы по коэффициентам регрессии делаются аналогично пункту 1.
Оцените с помощью F-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи
Оценку надежности уравнения регрессии в целом и показателя тесноты связи 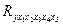 дает F-критерий Фишера:
дает F-критерий Фишера:
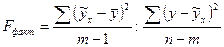 .
.
Для проверки значимости уравнения выдвигаем две гипотезы:
Н0: уравнение регрессии статистически не значимо;
Н1: уравнение регрессии статистически значимо.
По данным таблиц дисперсионного анализа, представленным на рисунке 1.5, 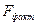 =32,8. Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5 %; об этом свидетельствует величина P – значение из этой же таблицы. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи
=32,8. Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5 %; об этом свидетельствует величина P – значение из этой же таблицы. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи 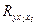 .
.
