Жылуөткізгіштік теңдеу

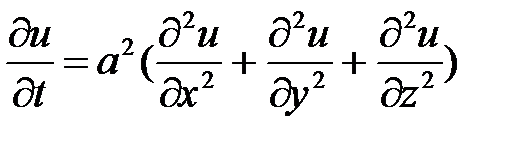, (4)

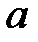-жылуөткізгіштік коэффициенті, 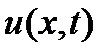-температура.

(4) теңдеу жылудың біртекті изотропті ортада таралуын және диффузия құбылысын сипатайды.

Бірретті (4) теңдеу келесі түрде жазылады:

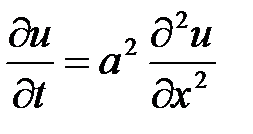
және жіңішке біртекті стержінде жылудың жайылуын сипатайды

Екіретті (4) теңдеу:

.

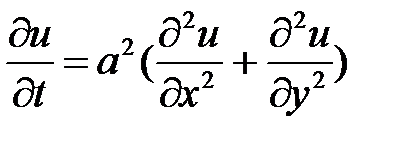Біртекті жұқа пластинада жылудың жайылуын сипатайды . (4) теңдеу параболалықтипіне жатады.

8.2.3. Пуассон теңдеуі:

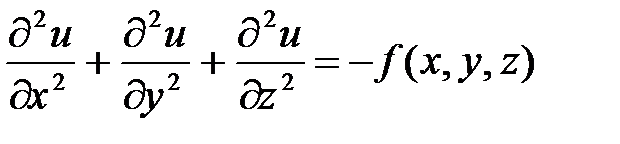, (5)

Біртекті изотоптық денеде жылудың жайылу стационардық процесін сипаттайды.

Жылу көзінің болмаған жағдайында (5) теңдеу - Лаплас теңдеуі болады:

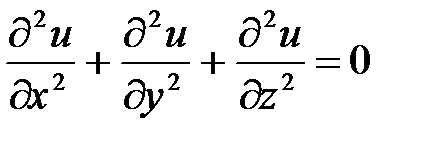. (6)

(5) және (6) – эллиптикалық типті теңдеулер.

Жалпы жағдайда (3)-(6) - теңдеулердің шешімі шексіз көп болады. Сондықтан мұндай теңдеулерді шешу үшін оларға қосымша бастапқы және шекаралық шарттар беріледі.

Егер бір айнымалы уақыттан тәуелді болса, оған қатысты шарт бастапқы шарт деп аталады. Келесі айнымалы кеңістіктегі кординаттар болып, тұрақтандырылған белгілі бір нүктелердегі мәндерді көрсетсе, оған қатысты шарт шекаралық шарт деп аталады.

Егер теңдеу тек қана кеңістіктік координаттардан тәуелді болса, яғни уақытқа байланыссыз өзгеретін процесстерді сипаттаса, онда стационар дифференциалдық теңдеу деп аталады. Оған Гельмгольц теңдеуі, Пуассон теңдеуі үшін Дирихле есебі жатады. Ал теңдеу уақыт айнымалысынан тәуелді болып, қандай да бір процестің уақыт өзгеруіне байланысты мәндерін анықтауға қатысты болса, онда стационар емес теңдеу деп аталады. Оған Толқын теңдеуі, жылуөткізгіштік теңдеуі жатады.

Математикалық есепкелесі үш шартты камтамасыз ету керек:

есеп шешімі болуы;

есеп шешімінің жалғыздығы;

есеп шешімінің орнықтылығы, яғни есеп деректерінің аз қүбылыстары шішімнің аз күбылыстарына әкелу тиіс.

Ос шартар орындалса, онда қойылған есеп кисынды.

8.3 Жылуөткiзгiштiк теңдеуді шешу үшiн айырымдық схемалар Жылуөткізгіштік теңдеуін қарастырайық

Еспеп қойылымы

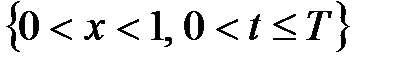облысындакелесі теңдеудің шешімін табу керек

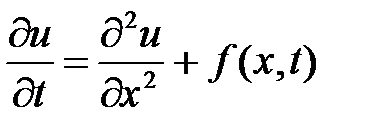, (7)

Шешім бастапқы шартқа

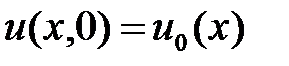(8)

Және шеттік шартқа сәйкес болуы қажет

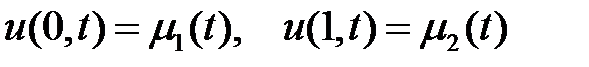(9)

Мында 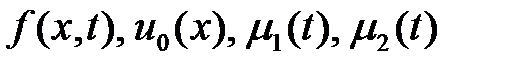- берілген функциялар.

Айқын схема.

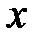айнымалмен тор құрылсын: 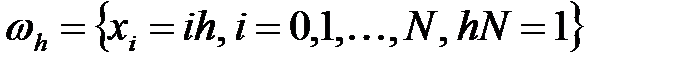, және 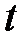айнымалымен, 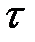қадамды тор: .

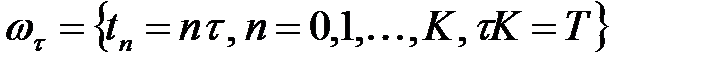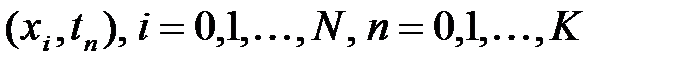нүктелер тордың түйіндерын құрады 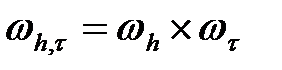, сурет 1.

0

tn

T

1

xi

t

h

1 – сурет. Кенестік-уақыттық тор.

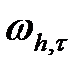торда анықталған 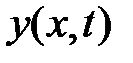- функция 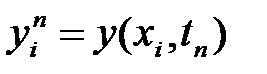белгіленеді. Дифференциальное теңдеу (7) аппроксимациаланады:

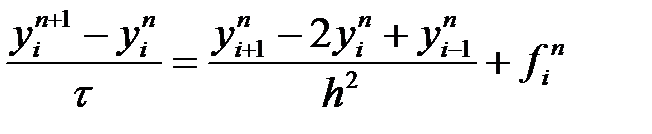, (10)

аппроксимация реті .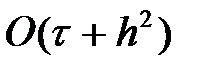

Есептің айырымдық схемасы:

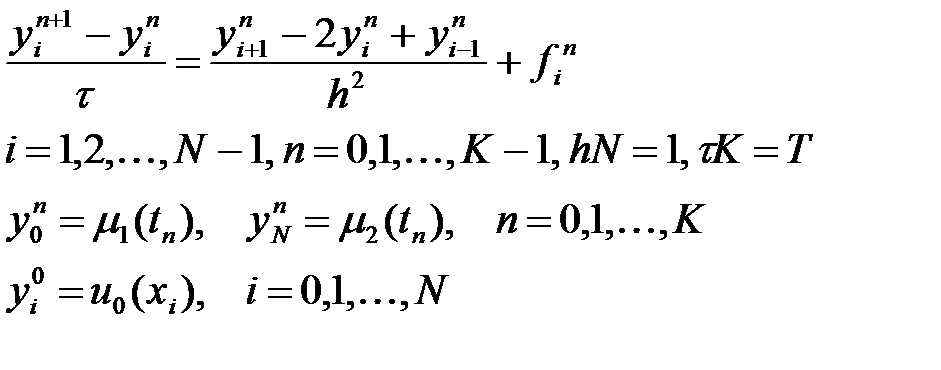. (11)

Нөлінші қабаттағы шешім бастапқы шартымен анықталады 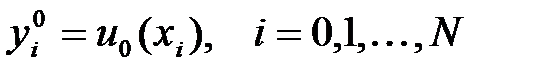. Егер шешім 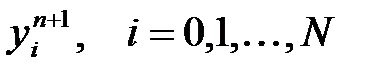n қабатта табылса, онда шешім 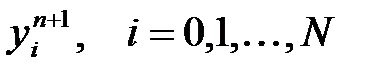n+1 қабатта айқын формуламен табылады:

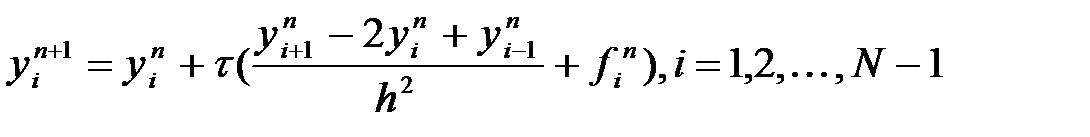, (12)

ал 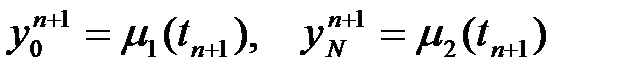шеткі шарттан анықталады.

(11) схеманың аппроксимация қателігі тең 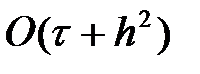. Айқын схеманы (11) тек қана 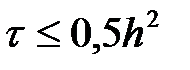шарт орындался қолдануға болады.

Айқын емес схема.

Жылуөткізгіштік теңдеуінің айқын емес схемасы

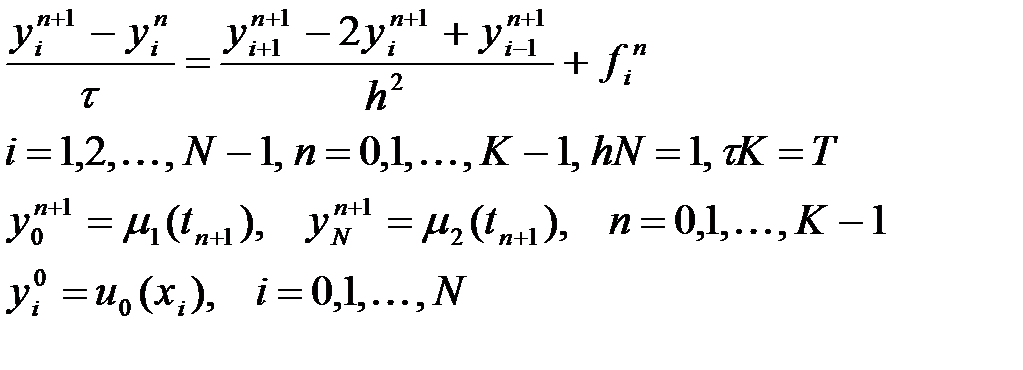(13)

Аппроксимация схемсының реті 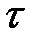бойынша 1, 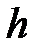бойынша 2. (13) жүйнең шешімі 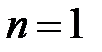басталады. 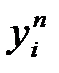- арқылы 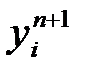табу үшін келесі жүйне шешу керек

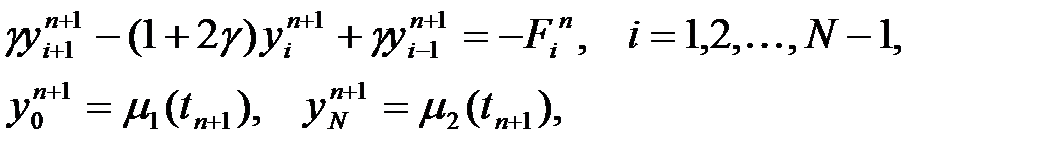(14)

мында .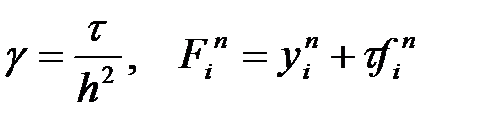

Бул жүйені қуалау әдісімен шешуге болады.

Бірпараметрлік схема. σ параметрін алсақ келесі айырымдық схема арқылы табылады

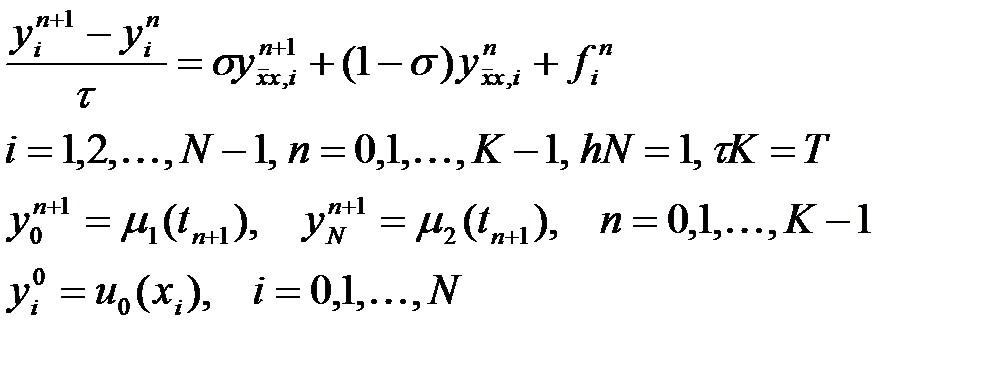(15)

мұнда .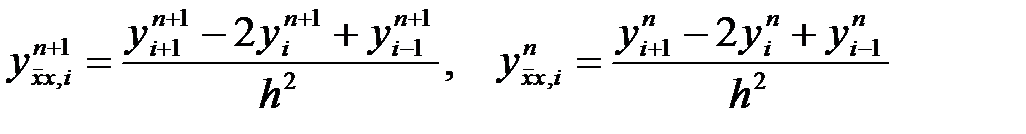

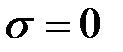болған жағдайда (15) айқын схема, 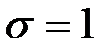- айқын емес. Егер 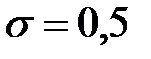болса схеманың аппроксимация реті .

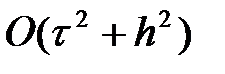8.3.3 Айнымалыларды бағыттау әдісі.

Көпөлшемді есептерді шешуге арналған әдістердің бірі, көпөлшемді әдістер бірөлшемдіге қатысты сипатқа негізделген, сонымен қатар ол өзіне оң мәнді айқын және айқын емес схемаларды сипаттайды: абсолютті тұрақтылық және қарапайым шешім. Бұл әдістің ішінде айырымдылық схемасына бір мысал келітсек, ол көбіне көлденең бойлай айырымдылық схемасы немесе Писмен-Рэчфорд схемасы деп аталады. Бұл схемада n қабатынан n+1 қабатына дейін екі кезеңде орындалады. Бірінші кезеңде жүйе теңдеуінен 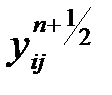аралық мәндері алынған.

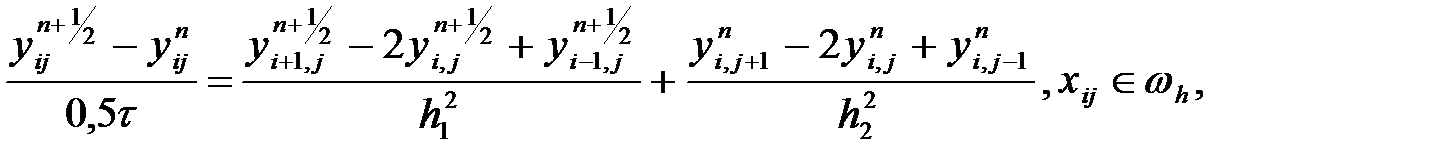(22)

Ал екінші кезеңде 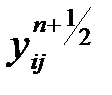табылған мәнін жүйе теңдеуінен 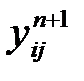табамыз

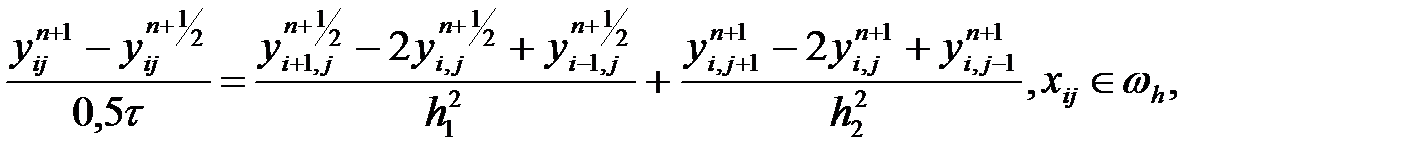(23)

(22) теңдеуі 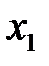айнымалысына қатысты айқын емес, ал (23) теңдеуі 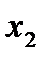айнымалысы бойынша болып келеді. Сондықтан (22), (23) теңдеулерін бірөлшемді қуалау әдісінің жүйелі қолданысымен шешуге болады, алдымен 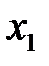бағыты бойынша, ал сосын 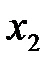бағыты бойынша.

(22)-(23) схемалары абсолютті тұрақты 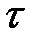және және 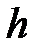бойынша екінші ретті суммарлы аппроксимацияға ие. Яғни, толық қабаттан жартылай қабатқа өту кезінде әрбір кеңістіктегі айырым уақытқа байланысты симметриялы болмайды және 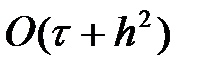қателігіне тең. Бірақ қабаттың екінші бөлігіндегі қателік біріншіні компенсирлейді, нәтижесінде толық қабаттан толық қателігі локалды аппроксимацияда бірқалыпты торларда болады .

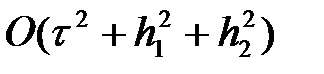1 мысал.Бірінші есепжылуөткізгіштік теңдеуін шешу:

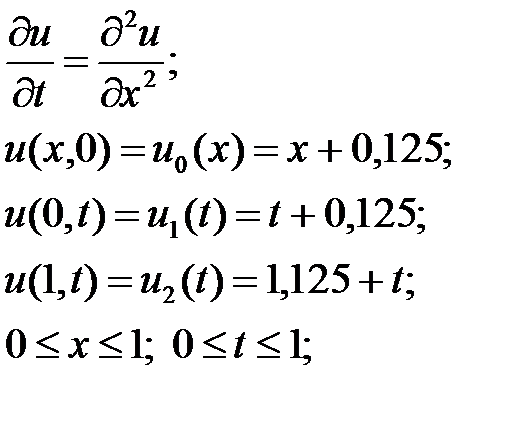
Шешуі:

Уақытқа байланысты τ=0,1 қадамына тең торын қарастырайық және h=0,1 қадамы x кеңістік қадамы бойынша алынады.

Аппроксимациялық теңдеуге қатысты айқын емес схеманы қолданамыз.

;

;

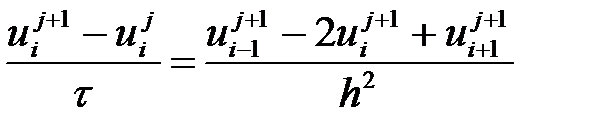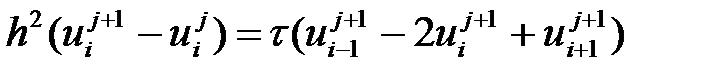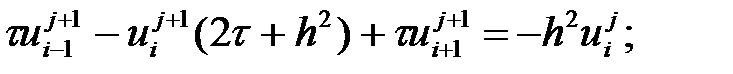
Бастапқы шартты аппроксимациялаймыз.

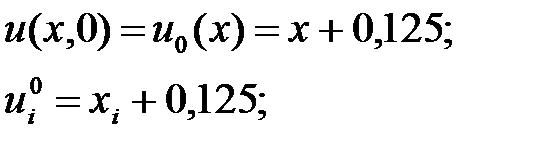
Келесі шарттын аппроксимациялаймыз.

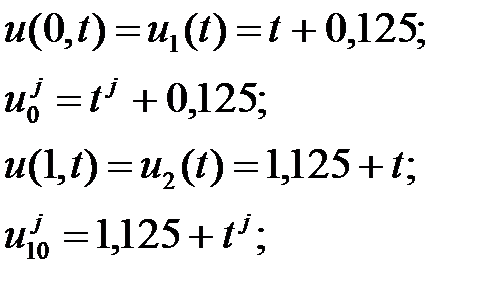
Осының нәтижесінде айырым есебі қойылды:

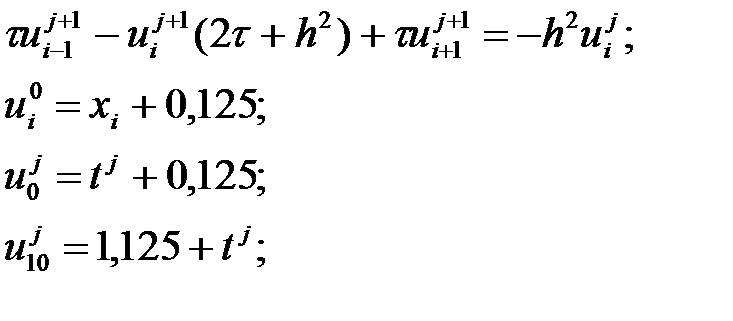
Бұл есеп қуалау әдісімен есептеледі. Қулаудың сәйкестілік шарты орындалды: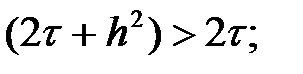

j=0 үшін функцияның мәні бастапқы шарттан табылады, j=1, …, 10 үшін функция мәні қуалау әдісінің көмегімен табылады. Қуалаудың нәтижесі j=1, 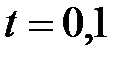үшін 1 кестеде көрсетілген.

1 кесте. Қуалау әдісінің жүзеге асуы.

i	xi	ai	bi	ci	αi	βi	yi	fi
	0,00	0,10	0,10	0,21			0,225	0,001
	0,10	0,10	0,10	0,21	0,00	0,23	0,301	0,002
	0,20	0,10	0,10	0,21	0,48	0,12	0,384	0,003
	0,30	0,10	0,10	0,21	0,62	0,09	0,473	0,004
	0,40	0,10	0,10	0,21	0,67	0,09	0,567	0,005
	0,50	0,10	0,10	0,21	0,70	0,10	0,665	0,006
	0,60	0,10	0,10	0,21	0,71	0,12	0,767	0,007
	0,70	0,10	0,10	0,21	0,72	0,14	0,873	0,008
	0,80	0,10	0,10	0,21	0,73	0,16	0,984	0,009
	0,90	0,10	0,10	0,21	0,73	0,18	1,101	0,01
	1,00	0,10	0,10	0,21	0,73	0,21	1,225	0,011

j=1, …, 10 үшін функция мәні қуалаудың көмегімен табылады, олар келесі 2 кестеде көрсетілген.

2 кесте. Есептеудің нәтижесі.

		1,13	1,18	1,25	1,32	1,41	1,50	1,61	1,72	1,85	1,98	2,13
	0,9	1,03	1,08	1,15	1,22	1,31	1,40	1,51	1,62	1,75	1,88	2,03
	0,8	0,93	0,98	1,05	1,12	1,21	1,30	1,41	1,52	1,65	1,78	1,93
	0,7	0,83	0,88	0,95	1,02	1,11	1,20	1,31	1,42	1,55	1,68	1,83
	0,6	0,73	0,78	0,85	0,92	1,01	1,10	1,21	1,32	1,45	1,58	1,73
	0,5	0,63	0,68	0,75	0,82	0,91	1,00	1,11	1,22	1,35	1,48	1,63
	0,4	0,53	0,58	0,65	0,73	0,81	0,91	1,01	1,13	1,25	1,38	1,53
	0,3	0,43	0,49	0,55	0,63	0,72	0,82	0,92	1,03	1,15	1,29	1,43
	0,2	0,33	0,39	0,46	0,55	0,64	0,73	0,84	0,95	1,06	1,19	1,33
	0,1	0,23	0,30	0,38	0,47	0,57	0,66	0,77	0,87	0,98	1,10	1,23
		0,13	0,23	0,33	0,43	0,53	0,63	0,73	0,83	0,93	1,03	1,13
	t/x		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
j/i

8.4 Эллипстикалық теңдеу