Определители второго и третьего порядка. Их свойства
Рассмотрим квадратную матрицу второго порядка
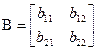 | 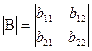 | |||
| (3) | и | (4) | ||
· Определителем второго порядка (4) квадратной матрицы (3) называется число 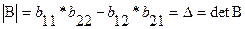 .
.
Например, 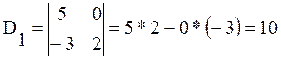 ,
,
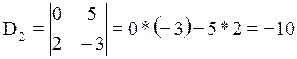
· Определителем квадратной матрицы третьего порядка называется число: 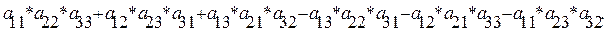
Чтобы запомнить какие произведения следует брать со знаком плюс, а какие со знаком минус, можно пользоваться следующим схематично изображенным правилом:
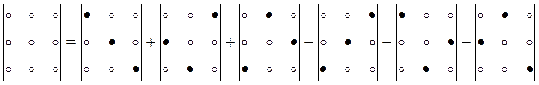
g Рассчитайте значения определителей:
1. 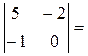
2. 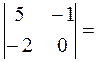
3. 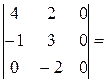
4. 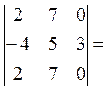
5. 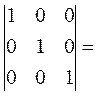
Свойства определителей.
1° Определитель не изменится, если строки определителя заменить соответствующими столбцами.
Докажем это на примере определителя второго порядка. Вычислим:
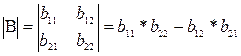 и
и 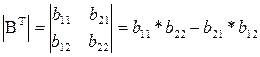
Поскольку 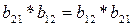 , то
, то 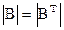
g Доказать самостоятельно для определителя третьего порядка:
2° Общий множитель элементов какой-либо строки (столбца) определителя может быть вынесен за знак определителя.
Действительно:
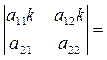
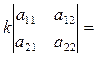
3° Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца) определителя, то определитель равен нулю.
g Самостоятельно докажите для определителя III порядка.
4° При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
g Самостоятельно доказать для определителя III порядка.
5° Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственно элементы другой строки (столбца), умноженные на одно и то же число (теорема о линейной комбинации параллельных рядов определителя).
Действительно, покажем на примере:
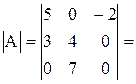
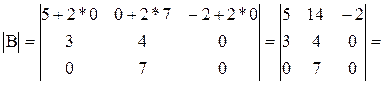
Алгебраические дополнения и миноры.
· Минором Mij элемента 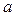 ij определителя третьего порядка называется определитель второго порядка, который получается, если в исходном определителе вычеркнуть строку i и столбец j, содержащие элемент
ij определителя третьего порядка называется определитель второго порядка, который получается, если в исходном определителе вычеркнуть строку i и столбец j, содержащие элемент 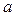 ij.
ij.
· Алгебраическим дополнением элемента 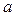 ij называется его минор, умноженный на (-1)k, где k=i+j;
ij называется его минор, умноженный на (-1)k, где k=i+j; 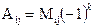 .
.
g Для матрицы 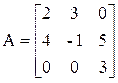 найдите алгебраические дополнения элементов
найдите алгебраические дополнения элементов 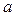 13,
13, 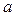 22,
22, 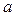 12,
12, 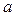 23:
23:
Вычисление определителя разложением по элементам строки (столбца).
· Теорема 1: Определитель третьего порядка равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения.
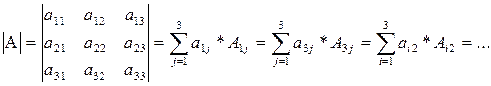
g Проверьте самостоятельно для i=2; j=1.
Доказательство.
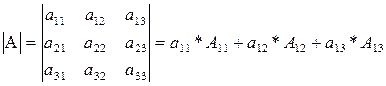
· Теорема 2: Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
· Квадратная матрица A называется невырожденной (неособой), если 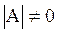 . Если же detA=0, то она называется вырожденной (особой).
. Если же detA=0, то она называется вырожденной (особой).
