Відомість обчислення координат
Практична робота № 6
«Обробка результатів теодолітної зйомки ділянки. Замкнутий теодолітний хід»
Мета завдання: навчитися обробляти польові матеріали: геодезичні журнали з результатами вимірювань кутів, довжин ліній та абрису; вираховувати координати точок теодолітних ходів, які будуть використані в подальшому для побудови плану теодолітної зйомки
Обладнання і приладдя: матеріали теодолітної зйомки, відомість обрахунку координат, ручки чорні діаметром 0,5,олівці твердо-м’які, т і 2 т,масштабна лінійка, трикутник, гумка, інженерний калькулятор, робочий зошит.
Найпростіша геодезична опорна мережа – геодезичний хід як сукупність точок, розміщених і закріплених на місцевості так, щоб забезпечити послідовне (від точки до точки) вимірювання віддалей між ними (сторін ходу), кутів, утворених цими сторонами, та перевищень між точками. Хід може бутирозімкнутим(якщо перша і остання точка не збігається) або замкнутим (якщо точка 1 ходу є і початковою і кінцевою). Замкнутий хід називають полігоном. Залежно від приладів, застосовуваних під час прокладання ходу, його називають теодолітним, нівелірним, мензульним.
Теодолітна зйомкаотримала свою назву від основного приладу, який застосовується при зйомці. Теодолітом вимірюють кути на місцевості і тому теодолітну зйомку називають ще кутовимірювальною.Окрім вимірювань кутів при зйомці ще здійснюють вимірювання ліній мірними стрічками та віддалемірами відповідної точності. Теодолітна зйомка широко використовується для отримання планів ділянок рівнинної місцевості з нескладною ситуацією. Для теодолітної зйомки на місцевості спочатку створюють знімальну мережу опорних точок у вигляді теодолітних ходів, які в геометричному відношенні являють собою систему ломаних ліній.
Теодолітний хід - це геодезична побудова (хід) у вигляді замкнутої або розімкнутої ламаної лінії на місцевості, в якій горизонтальні кути міряються теодолітами, а довжини сторін - землемірними стрічками, рулетками або світловіддалемірами.
Наприклад, для зйомки територій колективних підприємств по їх межах на місцевості складають замкнуті полігони. В середині полігонів часто прокладають так звані діагональні ходи, які слугують для контролю результатів кутових та лінійних вимірювань, а також для зйомки ситуації. Для зйомки окремих невеликих, витягнутих в одному напрямку, ділянок знімальною основою може бути розімкнутий теодолітний хід. Середня довжина ліній теодолітних ходів повинна бути біля 200-250 м з можливим відхиленням у мешу сторону до 50 м і в більшу до 400 м. В знімальних ходах кути вимірюються теодолітом повним прийомом, а ліній – мірними стрічками чи віддалемірами відповідної точності.
Теодолітний хід може бути доповненням до вже існуючої мережі й тоді координатийого початкової точки визначають з урахуванням координат найближчих пунктів цієї мережі (процес має назву прив’язкитеодолітного ходу). Не прив’язаний теодолітний хід до існуючої мережі називається вільним.
Перед початком вимірюваньточки теодолітного ходу, або точки повороту чи вершини ходу, закріплюється на місцевості.При виборі місцеположення точок керуються зручністю подальшого використання їх та забезпеченням довгострокового збереження. Закріплюють точки тимчасовими або постійними геодезичними знаками. За тимчасові знаки служать дерев’яні стовпи і кілки, металеві костилі та труби. Центри знаків маркірують (тобто визначають) фарбою або цвяхами. Тимчасові знаки використовують на невеликих ділянках, а також і тоді, коли нема необхідності в тривалому зберіганні.
Перед тим, як перейти до обчислень ходів, виконується перевірка польових записів в журналі вимірювань кутів та ліній. Знайдені в них помилки та прорахунки виправляються. При цьому не можна виправляти цифру на цифрі, слід неправильні цифри закреслити однією рискою, а правильні написати вище на вільному місці. Після кожного перевіреного результату робиться помітка про перевірку. Переписувати польові матеріали заборонено. Після цього складають схему ходу і на ній виписують всі кути із журналу і горизонтальні проекції. Всі значення довжин ліній і кутів обводять чорнилом чи чорною ручкою. Потім зі схеми переписують у відомість обчислення координат.
Надалі виконуються такі роботи:
ü ув’язують кути теодолітних ходів геодезичного обґрунтування;
ü обчислюють дирекційні кути сторін теодолітних ходів і визначають румби цих сторін;
ü здійснюють обчислення приростів координат;
ü вирівнюють прирости координат;
ü обчислюють координати точок полігона.
Завданням обрахункових робіт є не тільки отримання координат точок, а і паралельно проводиться контроль результатів польових вимірювань і оцінка їх точності, яка є показником якості виконаних вимірювань.
Порядок та послідовність виконання завдання:
1. Студент самостійно опрацьовує рекомендовану літературу.
2. Обрахунок результатів польових вимірювань проводиться в спеціальній формі - відомості обрахунку координат (табл.12.). Студент отримує схему теодолітного ходу і під час лабораторної роботи викреслює полігон замкнутого теодолітного ходу за варіантом (Додаток ).
3. Для прискорення обрахунків потрібно застосовувати допоміжні засоби: калькулятори, таблиці, графіки.
4. Записи слід вести акуратно, чорною ручкою. Розряди в багато значущих цифрах слід розділяти інтервалами. Цифри чисел, розташованих в колонку, повинні бути розміщені під відповідними цифрами вище розміщеного числа.
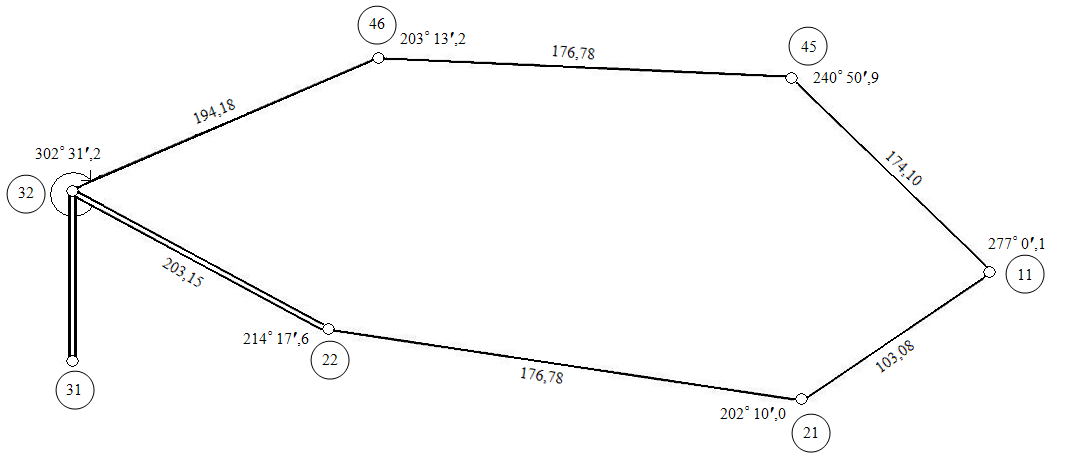
5. Порядок визначення координат точок замкнутого теодолітного ходу (рис. 70):
6. Порядок роботи розглянемо на прикладі ( див. табл.12, рис.70).
7. З виконаною лабораторною роботою студент приходить на кафедру для її захисту.
α32-22 = 132˚22′,4
Координати т. 32, 31
| № | Х | У |
| 10187,0 | 10200,0 | |
| 10050,0 | 10350,0 |
Рис. 70. Схема теодолітного полігона.
| № точ. | Виміряні кути | По-прав. | Врівноваж. кути | Дирекц. кути, T | Румби, r | Горизонт. проклада-ння | Обчисленні прирости | Врівноважені прирости | Координати | ||||||
| Δx | попр | Δy | попр | Δx | Δy | X | Y | ||||||||
| 57˚ 28,′8 | + 0,5′ | 57˚ 29,′3 | 10187,00 | 10200,00 | |||||||||||
| 132 24,4 | ПдСх 47˚ 35,′6 | 203,15 | -137,00 | 150,00 | -137,00 | 150,00 | |||||||||
| 145˚ 42,′4 | + 0,5′ | 145˚ 42,′9 | 10050,0 | 10350,0 | |||||||||||
| 166 41,5 | ПдСх 13˚ 18,′5 | 176,78 | -172,03 | 0,01 | 40,69 | -0,01 | -172,02 | 40,68 | |||||||
| 157˚ 50,′0 | + 0,5′ | 157˚ 50,′5 | 9877,98 | 10390,68 | |||||||||||
| 188 51,0 | ПдЗх 8˚ 51,′0 | 103,08 | -101,85 | 0,01 | -15,85 | -101,84 | -15,85 | ||||||||
| 82˚ 59,′9 | + 0,5′ | 82˚ 60,′4 | 9776,14 | 10374,83 | |||||||||||
| 285 50,6 | ПнЗх 105˚ 50,′6 | 174,10 | 47,53 | 0,01 | -167,48 | 47,54 | -167,48 | ||||||||
| 119˚ 9,′1 | + 0,5′ | 119˚ 9,′6 | 9823,68 | 10207,35 | |||||||||||
| 346 41,0 | ПнЗх 13˚ 19,′0 | 176,78 | 172,02 | 0,01 | -40,71 | 172,03 | -40,71 | ||||||||
| 156˚ 46,′8 | + 0,5′ | 156˚ 47,′3 | 9995,71 | 10166,64 | |||||||||||
| 9 53,7 | ПнСх 9˚ 53,′7 | 194,18 | 191,29 | 33,36 | 191,29 | 33,36 | |||||||||
| 10187,00 | 10200,00 | ||||||||||||||
Таблиця 12
Відомість обчислення координат
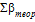 = 180˚(n-2)
= 180˚(n-2)
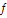 β =
β = 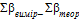
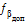 = ± 1,5·t’·
= ± 1,5·t’· 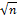
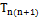 =
= 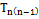 ±180˚-
±180˚- 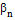
Δx=d·Cos(T)
| ПнСх | ПдСх | ПдЗх | ПнЗх |
| +Δx | -Δx | -Δx | +Δx |
| +Δy | +Δy | -Δy | -Δy |
Δу=d·Sin (T)
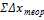 =0
=0
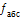 =
= 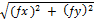 =
= 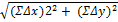
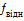 =
= 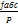 ≤
≤ 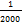
1) Якщо кути горизонтальні по ходу праві (внутрішні) то їх вписуємо у «Відомість замкнутого теодолітного ходу» в графу «2». У графі «1» назву точки. Наприклад, у нашому варіанті 6 точок (32, 22, 21, 11, 45, 46).Якщо кути ліві, як в нашому прикладі (див. рис. 70), то переводимо їх у праві за формулою:горизонтальний кут (лівий) = 360˚ - β , де β – це значення лівого кута за ходом теодолітної зйомки.
Підставимо у формулу:
1) 360˚ - 302˚ 31,′2 = 57˚ 28,′8;
2) 360˚ - 214˚ 17,′6 = 145˚ 42,′4;
3) 360˚ - 202˚ 10,′0 = 157˚ 50,′0;
4) 360˚ - 277˚ 0,′1 = 82˚ 59,′9;
5) 360˚ - 240˚ 50,′9 = 119˚ 9,′1;
6) 360˚ - 203˚ 13,′2 = 156˚ 46,′8.
Ми маємо випадок коли віднімаємо у 2-й дії кут 145˚ 42,′24″. Ці 24″ секунди треба перевести у мінути, тому 24 : 4 = 0,4′ (Рис. 71). Перевівши секунди у мінути, вписуємо отримані значення в колонку 2.

Рис. 71. Дії на мікрокалькуляторі, при перетворенні лівих кутів у праві
2) Знаходимо практичну суму горизонтальних кутів замкнутого теодолітного ходу.
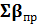 = 57˚ 28,′8 + 145˚ 42,′4+ 157˚ 50,′0 + 82˚ 59,′9 + 119˚ 9,′1 + 156˚ 46,′8 = 719˚ 57,′0
= 57˚ 28,′8 + 145˚ 42,′4+ 157˚ 50,′0 + 82˚ 59,′9 + 119˚ 9,′1 + 156˚ 46,′8 = 719˚ 57,′0
3) Проводимо ув’язку горизонтальних кутів полігону. Для цього знаходимо теоретичну суму кутів ( 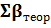 ) :
) :
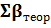 = 180˚(n - 2),
= 180˚(n - 2),
де, n – кількість виміряних кутів у полігоні.
У нашому прикладі 6 горизонтальних кутів:
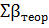 = 180˚(6 - 2) = 720˚
= 180˚(6 - 2) = 720˚
4) Знаходимо кутову похибку, яка підтвердить достовірність польових досліджень, за формулою :
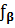 =
= 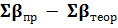 ,
,
де, 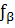 – кутова похибка.
– кутова похибка.
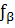 =719˚ 57,′0
=719˚ 57,′0 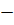 720˚ =
720˚ = 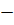 3′
3′
Внесення кутових поправок:
1) Вноситься в кожний кут порівно з протилежним знаком, тобто якщо похибка у зі знаком « 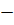 », то додаємо її до виміряного горизонтального кута, якщо ж вона зі знаком «+», то навпаки її віднімаємо.
», то додаємо її до виміряного горизонтального кута, якщо ж вона зі знаком «+», то навпаки її віднімаємо.
2) Поправки вносяться не в кожний виміряний кут, а лише в ті кути, до яких прилягають найкоротші відстані. Поправка вноситься у графу«3».
Спочатку вносять поправки на ті кути, які мають найбільше горизонтальне прокладання, або порівно розподіляють на всі кути, як в нашому прикладі:
3′ : 6 = + 0,5′
Вносимо в графу за знаком «+»
Наприклад:
57˚ 28,′8 + 0,5′ = 57˚ 29,′3 , або 57˚ 28,′8 + ( 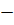 0,5′) = 57˚ 28,′3 , якщо поправка за знаком «
0,5′) = 57˚ 28,′3 , якщо поправка за знаком « 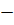 »
»
5) Вираховуємо за формулою допустиму поправку:
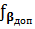 = ± 1,5·t′·
= ± 1,5·t′· 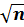 ,
,
де, t′ - подвоєна точність теодоліта.
n – кількість виміряних кутів.
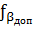 = 1,5·1′·
= 1,5·1′· 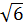 = 7′,2
= 7′,2
Якщо практична похибка допустима, то у виміряні кути вносять поправки, з таким розрахунком, щоб сума виправлених кутів була рівна теоретичній.
Для контролю із графи «4» додали всі кути. Їх сума дорівнювала 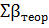 .
.
6) Вираховуємо дирекцій ний кут, за формулою:
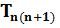 =
= 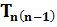 ± 180˚ -
± 180˚ - 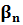 де
де
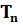 - дирекційний кут;
- дирекційний кут;
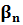 - горизонтальний кут;
- горизонтальний кут;
n– кількість виміряних кутів.
Із схеми перший дирекцій ний кут становить 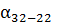 = 132˚22′,4. Вписуємо його у графу«5».
= 132˚22′,4. Вписуємо його у графу«5».
Далі вираховуємо дирекційний кут, за значенням врівноважених кутів (графа «4»):
1) 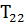 = 132˚24′,4 + 180˚ ± 145˚ 42,′9 = 166˚41,′5;
= 132˚24′,4 + 180˚ ± 145˚ 42,′9 = 166˚41,′5;
2) 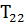 = 166˚41,′5 + 180˚ ± 157˚ 50,′5 = 188˚51, ′0;
= 166˚41,′5 + 180˚ ± 157˚ 50,′5 = 188˚51, ′0;
3) 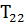 = 188˚51, ′0 + 180˚ ± 82˚ 60,′4 = 285˚50, ′6;
= 188˚51, ′0 + 180˚ ± 82˚ 60,′4 = 285˚50, ′6;
4) 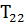 = 285˚50, ′6 + 180˚ ± 119˚ 9,′6 = 346˚41, ′0;
= 285˚50, ′6 + 180˚ ± 119˚ 9,′6 = 346˚41, ′0;
5) 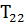 = 346˚41,′0 + 180˚ ± 156˚ 47,′3 = 9˚53,′7;
= 346˚41,′0 + 180˚ ± 156˚ 47,′3 = 9˚53,′7;
6) 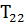 = 9˚53,′7 + 180˚ ± 57˚ 29,′3 = 132˚24,′4.
= 9˚53,′7 + 180˚ ± 57˚ 29,′3 = 132˚24,′4.
Якщо до дирекційного кута останньої лінії додати 180˚ і відняти кут у першій точці то повинні одержати початковий дирекцій ний кут першої лінії.
7) У «Відомість обчислення координат» записуємо горизонтальні проекції виміряних на місцевості ліній. У нашому прикладі їх 6 (203,15 м, 176,78м, 103,08 м, 174,10 м, 176,78 м, 194,18 м) ця сума P = 1028,07.
Для вирахування припростів координат дирекційні кути переводять у румби (рис. 72.).
1 – якщо дирекційний кут від 0˚ до 90˚ ,то r1 = α1, де r це румб
2 – якщо дирекційний кут від 90˚ до 180˚, то r2 =180˚ - α2
3 – якщо дирекційний кут від 180˚ до 270˚, то r3 = α3 - 180˚
4 – якщо дирекційний кут від270˚ до 360˚, то r4 =360˚ - α4
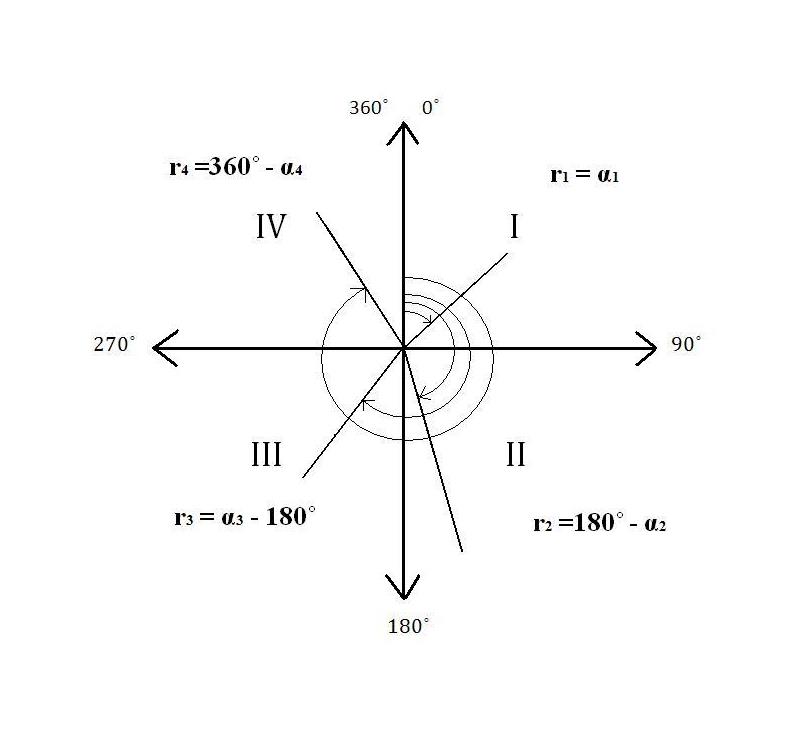
Рис. 72. Чверті румбів
Орієнтуючись на рис. 72 беремо із графи «5» значенняT кутів.
Наприклад кут 132˚24′,4 – він знаходиться у другій чверті тому, якщо підставити його у формулу, набуде вигляду:
1) 180˚ - 132˚24′,4 = Пд Сх 47˚ 35′,6 (відповідно і для решти кутів);
2) 180˚ - 166˚41,′5 = ПдСх 13˚ 18,′5;
3) 188˚51, ′0 - 180˚ = ПдЗх 8˚ 51,′0;
4) 360˚ - 285˚50, ′6 = ПнЗх 105˚ 50,′6;
5) 360˚ - 346˚41,′0 = ПнЗх 13˚ 19,′0;
6) 9˚53,′7 = ПнСх 9˚ 53,′7.
9) Вираховуємо прирости координат Δx та Δy за формулами:
Δx=d·Cos(r)
Δx=d·Sin (r) , де
d – горизонтальне прокладення.
Cos(r), Sin (r) = косинус або синус румба.
Тоді на калькуляторі виконуємо такі дії :
Δx = 203,15 * (cos47˚ 35′,6) = 203,15 * 0,73 = -137,00
Беремо cos на калькуляторі і набираємо значення румба з графи «6» або значення дирекційного кута з графи «5» ( Рис. 74, 75). Значення будуть ідентичні.
На калькуляторі обов’язково повинен стояти значок D – degrees (англ. –«градуси»), (рис. 73).
Якщо ж замість значка D обрані R (radian) або G (gradient) то за допомогою кнопки Mode обираємо D(degrees).

Рис. 73. Налаштування калькулятора
У нашому прикладі ми обираємо косинус дирекційного кута (рис. 74):
1)203,15 * (cos132˚24′,4 ) = 203,15 * 0,73 = -137,00
2) 176,78 * (cos166˚41,′5 ) = -172,03
3) 103,08 * (cos188˚51, ′0 ) = -101,85
4) 174,10 * (cos285˚50, ′6 ) = 47,53
5) 176,78 * (cos346˚41,′0) = 172,02
6) 194,18 * (cos9˚53,′7 ) = 191,29

Рис. 74. Дії на калькуляторі при взятті косинуса дирекційного кута

Рис. 75. Дії на калькуляторі при взятті косинуса румба
Чинимо відповідні дії з синусами та заносимо отримані результати у графи«8» та «10».

Рис. 4 Дії на калькуляторі при взятті синуса румба
Якщо значення румба наприклад ПдСх 47˚ 35′,6 то його значення по таблиці 3 буде зі знаком « 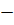 » ( табл. 3).
» ( табл. 3).
Таблиця 3
| ПнСх | ПдСх | ПдЗх | ПнЗх |
| +Δx | -Δx | -Δx | +Δx |
| +Δy | +Δy | -Δy | -Δy |
10) Розкидаємо поправку.
Всі значення з графи «8» зі знаком « 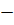 » та «+» додаємо окремо одне від одного, одержані результати порівнюємо та отримуємо похибку:
» та «+» додаємо окремо одне від одного, одержані результати порівнюємо та отримуємо похибку:
+410,88 = 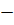 410,84
410,84
Аналогічні дії проводимо у графі «10».
Поправка знаходиться шляхом віднімання від суми додатних значень суму від’ємних:
410,84 – 410,88 = -0,04.
Поправку розкидаємо на найменші значення d з протилежним знаком. Тіж дії виконуємо у графі «11».
Врівноважені прирости записуємо відповідно у графи «12» і «13».
11) Потрібно також здійснити контроль:
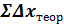 = 0
= 0
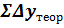 = 0
= 0
Δx: 410,86 - 410,86 = 0,00
Δy: 224,04 - 224,04 = 0,00
Для контролю в замкнутому полігоні знаходять алгебраїчну суму за Δx і Δy, яка буде виражати практичну похибку в приростах координат ( 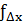 і
і 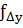 ). Щоб переконатись у достовірності виконання вимірювань знаходять абсолютну похибку (
). Щоб переконатись у достовірності виконання вимірювань знаходять абсолютну похибку ( 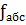 ) за формулою:
) за формулою:
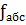 =
= 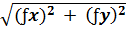 =
= 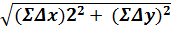 , а відносну
, а відносну 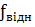 =
= 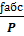 ≤
≤ 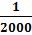 , де,P – периметр полігону (сума всіх сторін в багатокутнику)
, де,P – периметр полігону (сума всіх сторін в багатокутнику)
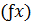 - обчислені прирости по Δx
- обчислені прирости по Δx
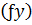 - обчислені прирости по Δy
- обчислені прирости по Δy
Наші поправки Δx = - 0,04 , Δy = +0,01. Підставляємо у формулу:
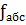 =
= 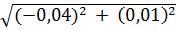 =
= 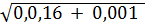 = 0,04
= 0,04
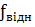 =
= 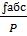 =
= 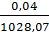 ~
~ 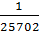
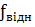 =
= 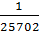 ≤
≤ 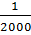
Тобто 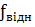 допустима у тому випадку коли відношення
допустима у тому випадку коли відношення 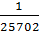 буде не більшим за
буде не більшим за 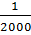
12)Координати точок вираховують за формулами:
Xк = Xк-1± Δx
Yк = Yк-1 ± Δy
Записуємо зі схеми полігону координати X таY і вписуємо у графи «14» і «15».
Наприклад:
X = 10187,0 Y = 10200,0
X = 10050,0 Y = 10350,0
Обрахунок проводимо таким чином:
1) 10187,00 + (-137,00) = 10050,0
2) 10050,0 + (-172,03) = 9877,98
3) 9877,98 + (-101,85) = 9776,14
4) 9776,14 + 47,53 = 9823,68
5) 9823,68 + 10187,00 = 9995,71
6) 9995,71 + 191,29 = 10187,00
Якщо до координати останньої точки в полігоні додати чи відняти приростки на останню лінію, то одержимо координати першої точки. Це і буде контролем вирахування координат.
Ті самі дії з відповідними числами проводимо з координатамиY.
Література:
1. Бакканова В.В. Геодезия. – М.: Недра, 1980.
2. Ганьшин В.Н. Простейшие измерения на месности. – М.: Недра,1973. –144с.
3. Ганьшин В.Н., Лебедева С.М, Хренов Л.С. Практикум по геодезии. – М.: Недра,1966. – 415 с.
4. Геодезія. Терміни та визначення. ДСТУ 2393-94.– К.: Держстандарт України, 1994.- 64с.
5. Гиршберг М.А. Геодезия.Ч.1. – М.: Недра, 1967.
6. Голубева З. С., Калошина О.В., Соколова Н.И. Пособие к лабораторно-практическим занятиям по геодезии. – М.: «Сельхоз-издат», 1957. – 182с.
7. Голубкін В.М., Соколов Н.І., Палехін І.М., Соффер М.І. Геодезія. – К.: «Вища школа», 1970.– 444с.
8. ГОСТ 10529-63.Теодолиты. Типы. Основные параметры и технические требования.
9. Лапкина Н.А. Практические работы по топографии и картографии. – М.: «Просвещение»,1971. – 174с.
10. Маслов А.В., Ларченко Е.Г., Гордеев А.В., Александров Н.Н. Геодезия. В 3-х частях . – Ч. 1. – М.: Из-дво геодез. лит., 1958. – 512 с.
11. Пастух В.В., Виноградов Г.Ф. Основи топографії: Підручник.– К.: ВЦ «Київський університет», 2000.– 327с.
12. Практикум по геодезии / В.В. Баканова, Я.Б. Карликин, Г.К. Павлова, М.С. Черемисин : Учеб. Пособие для вузов. 2-е узд., перераб. и доп. – М.: Недра, 1983.– 456с.
13. Практикум по геодезии / Под. ред. Бакановой В.В. – Недра, 1983.
14. Славачевский К. А. Пособие к практическим занятиям по геодезии. –М.,1962.– С. 9– 13.
15. Справочник геодезиста / Под ред. В. Д. Большакова, Г. П. Левчука. – М.: Недра, 1975.
«ТЕОДОЛІТНА ЗЙОМКА»
Практична робота № 6
«Обробка результатів теодолітної зйомки ділянки. Замкнутий теодолітний хід»
Мета завдання: навчитися обробляти польові матеріали: геодезичні журнали з результатами вимірювань кутів, довжин ліній та абрису; вираховувати координати точок теодолітних ходів, які будуть використані в подальшому для побудови плану теодолітної зйомки
Обладнання і приладдя: матеріали теодолітної зйомки, відомість обрахунку координат, ручки чорні діаметром 0,5, олівці твердо-м’які, Н і Н2 , масштабна лінійка, трикутник, гумка, інженерний калькулятор, робочий зошит.
Найпростіша геодезична опорна мережа – геодезичний хід як сукупність точок, розміщених і закріплених на місцевості так, щоб забезпечити послідовне (від точки до точки) вимірювання віддалей між ними (сторін ходу), кутів,утворених цими сторонами, та перевищень між точками. Хід може бути розімкнутим(якщо перша і остання точка не збігається) або замкнутим (якщо точка 1 ходу є і початковою і кінцевою). Замкнутий хід називають полігоном.
Теодолітна зйомка отримала свою назву від основного приладу, який застосовується при зйомці. Теодолітом вимірюють кути на місцевості і тому теодолітну зйомку називають ще кутовимірювальною. Окрім вимірювань кутів при зйомці ще здійснюють вимірювання ліній мірними стрічками та віддалемірами відповідної точності. Теодолітна зйомка широко використовується для отримання планів ділянок рівнинної місцевості з нескладною ситуацією. Для теодолітної зйомки на місцевості спочатку створюють знімальну мережу опорних точок у вигляді теодолітних ходів, які в геометричному відношенні являють собою систему ломаних ліній.
Теодолітний хід - це геодезична побудова (хід) у вигляді замкнутої або розімкнутої ламаної лінії на місцевості, в якій горизонтальні кути міряються теодолітами, а довжини сторін - землемірними стрічками, рулетками або світловіддалемірами.
Наприклад, для зйомки територій колективних підприємств по їх межах на місцевості складають замкнуті полігони. В середині полігонів часто прокладають так звані діагональні ходи, які слугують для контролю результатів кутових та лінійних вимірювань, а також для зйомки ситуації. Для зйомки окремих невеликих, витягнутих в одному напрямку, ділянок знімальною основою може бути розімкнутий теодолітний хід. Середня довжина ліній теодолітних ходів повинна бути біля 200-250 м з можливим відхиленням у мешу сторону до 50 м і в більшу до 400 м. В знімальних ходах кути вимірюються теодолітом повним прийомом, а ліній – мірними стрічками чи віддалемірами відповідної точності.
Теодолітний хід може бути доповненням до вже існуючої мережі й тоді координати його початкової точки визначають з урахуванням координат найближчих пунктів цієї мережі (процес має назву прив’язки теодолітного ходу). Не прив’язаний теодолітний хід до існуючої мережі називається вільним.
Перед початком вимірювань точки теодолітного ходу, або точки повороту чи вершини ходу, закріплюється на місцевості.При виборі місцеположення точок керуються зручністю подальшого використання їх та забезпеченням довгострокового збереження. Закріплюють точки тимчасовими або постійними геодезичними знаками. За тимчасові знаки служать дерев’яні стовпи і кілки, металеві костилі та труби. Центри знаків маркірують (тобто позначають) фарбою або цвяхами. Тимчасові знаки використовують на невеликих ділянках, а також і тоді, коли нема необхідності в тривалому збереженні даного пункту.
Перед тим, як перейти до обчислень ходів, виконується перевірка польових записів в журналі вимірювань кутів та ліній. Знайдені в них помилки та прорахунки виправляються. При цьому не можна виправляти цифру на цифрі, слід неправильні цифри закреслити однією рискою, а правильні написати вище на вільному місці. Після кожного перевіреного результату робиться помітка про перевірку. Переписувати польові матеріали заборонено. Після цього складають схему ходу і на ній виписують всі кути із журналу і попередньо обчислені горизонтальні проекції відстаней. Всі значення довжин ліній і кутів обводять чорнилом чи чорною ручкою. Потім з польового журналу переписують всі необхідні значення у журнал обчислення координат точок теодолітного ходу.
Надалі виконуються такі роботи:
ü ув’язують виміряні кути теодолітних ходів;
ü обчислюють дирекційні кути сторін теодолітних ходів і визначають румби цих сторін;
ü здійснюють обчислення приростів координат;
ü вирівнюють прирости координат;
ü обчислюють координати точок полігона.
Завданням розрахункових робіт є не тільки отримання координат точок, а і паралельно проводиться контроль результатів польових вимірювань і оцінка їх точності, яка є показником якості виконаних вимірювань.
Порядок та послідовність виконання завдання:
8. Студент самостійно опрацьовує рекомендовану літературу.
9. На основі результатів польових вимірювань проводиться розрахунок координат точок у спеціальній формі - відомості обрахунку координат точок теодолітного ходу, після чого викреслює полігон замкнутого теодолітного ходу за отриманими результатами. Вихідні дані знаходяться в додатку № .
10. Для прискорення обрахунків потрібно застосовувати допоміжні засоби: калькулятори, таблиці, графіки.
11. Записи слід вести акуратно, чорною ручкою. Розряди в багато значущих цифрах слід розділяти інтервалами. Цифри чисел, розташованих в колонку, повинні бути розміщені під відповідними цифрами вище розміщеного числа.
12. З виконаною лабораторною роботою студент приходить на кафедру для її захисту.
13. Порядок роботи розглянемо на прикладі ( див. табл.12, рис.70).
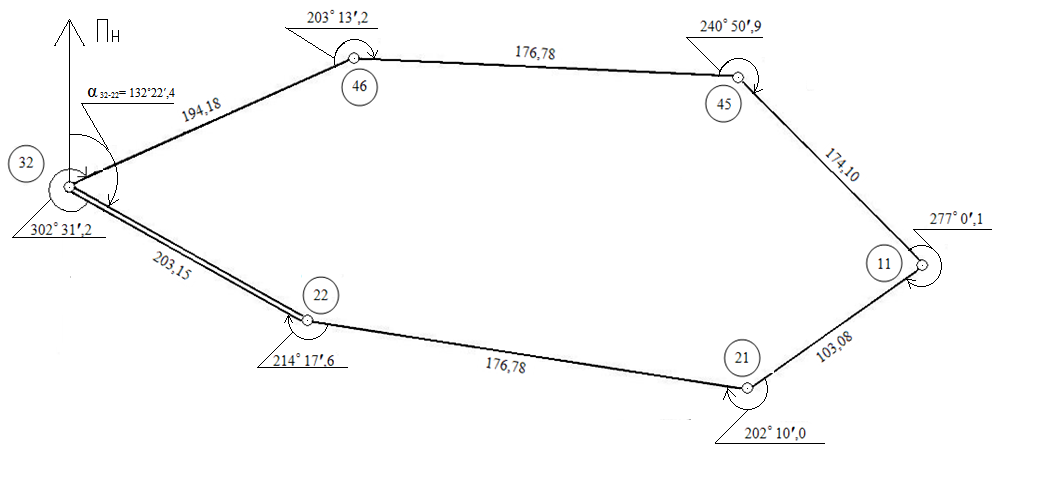
Координати т. 32
| № | Х | У |
| 10187,0 | 10200,0 |
α 32-22 = 132˚22′,4
Рис. 70. Схема теодолітного полігона.
1) Якщо кути горизонтальні по ходу праві то їх вписуємо у «Відомість замкнутого теодолітного ходу» в графу «2». У графі «1» назву точки. Наприклад у нашому варіанті 6 точок (32, 22, 21, 11, 45, 46).
Якщо кути ліві, як в нашому прикладі (див схему 1), то переводимо їх у праві за формулою:
Горизонтальний кут лівий = 360˚ - β ,
де β – це значення правого кута за ходом теодолітної зйомки.
Підставимо у формулу:
7) 360˚ - 302˚ 31,′2 = 57˚ 28,′8
8) 360˚ - 214˚ 17,′6 = 145˚ 42,′4
9) 360˚ - 202˚ 10,′0 = 157˚ 50,′0
10) 360˚ - 277˚ 0,′1 = 82˚ 59,′9
11) 360˚ - 240˚ 50,′9 = 119˚ 9,′1
12) 360˚ - 203˚ 13,′2 = 156˚ 46,′8
Ми маємо випадок коли віднімаємо у 2-й дії кут 145˚ 42′24″. В даному випадку 24″ секунди треба перевести у десяті мінути, тому 24 : 6 = 0,4′.Перетворивши секунди у десяті мінути, вписуємо отримані значення в колонку 2.

Рис. 2. Дії на інженерному калькуляторі, при перетворенні лівих кутів у праві.
2) Знаходимо практичну суму горизонтальних кутів замкнутого теодолітного ходу.
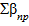 = 57˚ 28,′8 + 145˚ 42,′4+ 157˚ 50,′0 + 82˚ 59,′9 + 119˚ 9,′1 + 156˚ 46,′8 = 719˚ 57,′0
= 57˚ 28,′8 + 145˚ 42,′4+ 157˚ 50,′0 + 82˚ 59,′9 + 119˚ 9,′1 + 156˚ 46,′8 = 719˚ 57,′0
3) Проводимо ув’язку горизонтальних кутів полігону. Для цього знаходимо теоретичну суму кутів ( 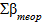 ) :
) :
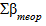 = 180˚(n - 2) ,
= 180˚(n - 2) ,
де, n – кількість виміряних кутів у полігоні.
У нашому прикладі 6 горизонтальних кутів:
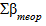 = 180˚(6 - 2) = 720˚
= 180˚(6 - 2) = 720˚
4) Знаходимо кутову похибку, яка підтвердить достовірність польових досліджень, за формулою :
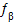 =
= 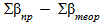 ,
,
де 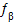 – кутова похибка.
– кутова похибка.
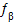 =
=  719˚ 57,′0
719˚ 57,′0  720˚ =
720˚ = 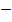 3′
3′
Внесення кутових поправок:
3) Вноситься в кожний кут рівномірно з протилежним знаком, тобто якщо похибка зі знаком « 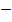 », то додаємо її до виміряного горизонтального кута, якщо ж вона зі знаком «+», то навпаки її віднімаємо.
», то додаємо її до виміряного горизонтального кута, якщо ж вона зі знаком «+», то навпаки її віднімаємо.
4) Поправки вносяться в кожний виміряний кут. Але є випадки, коли величина поправки невелика, то вносять її лише в ті кути до яких прилягають найкоротші відстані.
Поправка вноситься у колонку 3.
Спочатку вносять поправки на ті кути, які мають найменше горизонтальне прокладання, або порівно розподіляють на всі кути, як в нашому прикладі:
3′ : 6 = + 0,5′
Вносимо в графу за знаком «+»
Наприклад:
57˚ 28,′8 + 0,5′ = 57˚ 29,′3 ,
5) Вираховуємо за формулою допустиму поправку
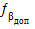 = ± 1,5·t′·
= ± 1,5·t′· 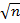 ,
,
де, t′ - подвоєна точність теодоліта.
n – кількість виміряних кутів.
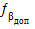 = 1,5·1′·
= 1,5·1′· 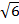 = 7, ′2
= 7, ′2
Якщо практична похибка допустима, то у виміряні кути вносять поправки, з таким розрахунком, аби сума виправлених кутів була рівна теоретичній.
Для контролю із графи 4 додали всі кути. Їх сума дорівнювала 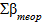 .
.
6) Вираховуємо дирекцій ний кут, за формулою:
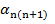 =
= 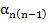 ± 180˚
± 180˚ 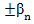 де,
де,
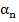 - дирекційний кут;
- дирекційний кут;
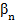 - горизонтальний кут;
- горизонтальний кут;
n – кількість виміряних кутів.
Із схеми перший дирекцій ний кут становить 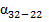 = 132˚22′,4. Вписуємо його у колонку 5.
= 132˚22′,4. Вписуємо його у колонку 5.
Далі вираховуємо дирекційний кут, за значенням врівноважених кутів (колонка 4). Відповідно до того ліві кути чи праві за ходом, необхідно використовувати наступні формули:
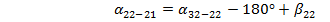 - формула для лівих по ходу кутів;
- формула для лівих по ходу кутів;
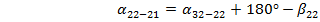 - формула для правих по ходу кутів.
- формула для правих по ходу кутів.
Отже виконуємо розрахунок дирекційних кутів за формулою для лівих кутів:
7) 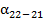 = 132˚22′,4 - 180˚ + 145˚ 42,′9 = 98˚05,′3
= 132˚22′,4 - 180˚ + 145˚ 42,′9 = 98˚05,′3
8) 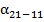 = 166˚41,′5 - 180˚ + 157˚ 50,′5 = 75˚55,′8
= 166˚41,′5 - 180˚ + 157˚ 50,′5 = 75˚55,′8
9) 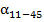 = 188˚51, ′0 - 180˚ + 82˚ 60,′4 = 338˚56,′2
= 188˚51, ′0 - 180˚ + 82˚ 60,′4 = 338˚56,′2
10) 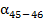 = 285˚50, ′6 - 180˚ + 119˚ 9,′6 = 278˚05,′8
= 285˚50, ′6 - 180˚ + 119˚ 9,′6 = 278˚05,′8
11) 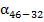 = 346˚41,′0 - 180˚ + 156˚ 47,′3 = 254˚53,′1
= 346˚41,′0 - 180˚ + 156˚ 47,′3 = 254˚53,′1
12) 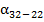 = 9˚53,′7 - 180˚ + 57˚ 29,′3 = 132˚22,′4
= 9˚53,′7 - 180˚ + 57˚ 29,′3 = 132˚22,′4
Якщо до дирекційного кута останньої лінії відняти 180˚ і додати кут у першій точці то повинні одержати початковий дирекцій ний кут першої лінії.
7) У «Відомість обчислення координат» записуємо горионтальні проекції виміряних на місцевості ліній. У нашому прикладі їх 6 (203,15 м, 176,78м, 103,08 м, 174,10 м, 176,78 м, 194,18 м) периметр P = 1028,07.
Для вирахування припростів координат дирекційні кути переводять у румби
1 – якщо дирекційний кут від 0˚ до 90˚ то r1 = α1, де r це румб
2 – якщо дирекційний кут від 90˚ до 180˚ то r2 =180˚ - α2
3 – якщо дирекційний кут від 180˚ до 270˚ то r3 = α3 - 180˚
4 – якщо дирекційний кут від270˚ до 360˚ то r4 =360˚ - α4

Рис. 2 Чверті румбів
Якщо значення румба наприклад ПдСх 47˚ 35′,6 то його значення по таблиці буде зі знаком « 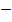 ».
».
| ПнСх | ПдСх | ПдЗх | ПнЗх |
| +Δx | -Δx | -Δx | +Δx |
| +Δy | +Δy | -Δy | -Δy |
Орієнтуючись на рис. 2 беремо із графи 5 значення α кутів.
Наприклад кут 132˚22′,4 > 90˚, тому він знаходиться у другій чверті, якщо підставити його у формулу, то вона набуде вигляду:
180˚ - 132˚22′,4 = Пд Сх 47˚ 37′,6
Так само і для інших кутів (див Рис. 1)
98˚05,′3 = ПнСх 98˚ 05,′3
75˚55, ′8 - 180˚ = ПнСх 75˚ 55,′8
360˚- 338˚56, ′2 = ПнЗх 22˚ 03,′8
360˚ - 278˚05,′8 = ПнЗх 81˚ 54,′5
254˚53,′1-180˚ = ПдЗх 74˚ 53,′1
9) Вираховуємо прирости координат Δx та Δy за формулами:
Δx=d·Cos(α)
Δx=d·Sin (α) , де
d – горизонт прокладення
Cos(α), Sin (α) = косинус або синус дирекційного кута.
Тоді на калькуляторі чинимо такі дії :
Δx = 203,15 * cos 47˚ 35′,6 = 203,15 *(- 0,674) = -136,92
Беремо cos на калькуляторі і набираємо значення дирекційного кута з графи 5.
На калькуляторі обов’язково повинен стояти значок D – degrees (англ. - градуси).
Якщо ж замість значка D обрані R (radian) або G (gradient) то за допомогою кнопки «Mode» обираємо degrees.

Рис. 2. Налаштування калькулятора
1) ΔX22 = 203,15 * cos 132˚ 22′,4 = -136,92
2) ΔX21 = 176,78 * cos 98˚05,′3 = -24,87
3)Δ X11 = 103,08 * cos 75˚55, ′8 = 25,06
4) ΔX45 = 174,10 * cos 338˚56, ′2 = 162,47
5) ΔX46 = 176,78 * cos 278˚405,′8 = 24,9
6) ΔX32 = 194,18 * cos 254˚53,′6 = -50,63


Рис. 3 Дії на калькуляторі при взятті косинуса дирекційного кута
Чинимо відповідні дії з синусами та заносимо отримані результати у колонки 8 та 10 відповідно.

Рис. 4 Дії на калькуляторі при взятті синуса румба
10) Розкидаємо поправку.
Знаходимо суму всіх значень з графи 8 враховуючи знаки « 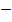 » та «+» та отримуємо суму приростів координат по Δx :
» та «+» та отримуємо суму приростів координат по Δx :
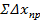 = (-136,92) + (-24,87) + 25,06 + 162,47 + 24,9 + (-50,63) = +0,01
= (-136,92) + (-24,87) + 25,06 + 162,47 + 24,9 + (-50,63) = +0,01
Аналогічні дії проводимо у графі 10.
Сума знаходиться шляхом додавання всіх значень приростів по Δy:
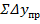 = 150,08 + 175,02 + 100 + (-62,57) + (-175,02) + (-187,46) = +0,05.
= 150,08 + 175,02 + 100 + (-62,57) + (-175,02) + (-187,46) = +0,05.
Потрібно також здійснити контроль:
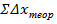 = 0
= 0
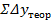 = 0
= 0
Δx: (-136,92) + (-24,87) + 25,05 + 162,47 + 24,9 + (-50,63)= 0,00
Δy: 150,08 + 175,01 + 99,99 + (-62,58) + (-175,03) + (-187,47) = 0,00
Для контролю в замкнутому полігоні знаходять різницю 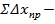
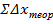 та
та 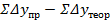 , яка буде виражати практичну похибку в приростах координат (
, яка буде виражати практичну похибку в приростах координат ( 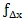 і
і 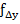 відповідно). Відповідно до цієї похибки розкидаємо поправку на найменші значення d з протилежним знаком (див табл. 1). Ті ж дії виконуємо у графі 11.
відповідно). Відповідно до цієї похибки розкидаємо поправку на найменші значення d з протилежним знаком (див табл. 1). Ті ж дії виконуємо у графі 11.
Врівноважені прирости записуємо у графи 12 і 13 відповідно.
Щоб переконатись у достовірності виконання вимірювань знаходять абсолютну похибку ( 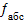 ) за формулою:
) за формулою:
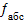 =
= 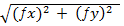 , а відносну
, а відносну 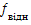 =
= 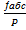 ≤
≤ 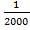
Де P – периметр полігону (сума всіх сторін в багатокутнику)
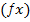 – різниця
– різниця 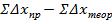
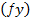 – різниця
– різниця 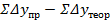
Наші поправки 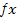 = 0,01 ,
= 0,01 , 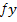 = +0,05. Підставляємо:
= +0,05. Підставляємо:
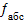 =
= 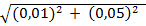 =
= 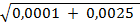 = 0,05
= 0,05
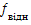 =
= 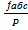 =
= 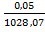 ~
~ 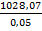
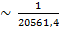
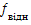 =
= 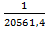 ≤
≤ 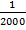
Тобто 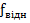 допустима у тому випадку коли відношення
допустима у тому випадку коли відношення 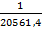 буде меншим або рівним
буде меншим або рівним 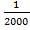
11) Координати точок вираховують за формулами:
Xк = Xк-1 + Δx
Yк = Yк-1 + Δy
Записуємо зі схеми полігону початкові координати X та Y і вписуємо у графи 14 і 15.
Наприклад:
X32 = 10187,00 Y32 = 10200,00
Обрахунок проводимо таким чином:
1) X22 = 10187,00 + (-136,92) = 10050,08
2) X21 = 10050,08 + (-24,87) = 10025,21
3) X11 = 10025,21 + 25,05 = 10050,26
4) X45 = 10050,26 + 162,47 = 10212,73
5) X46 = 10212,73 + 24,9 = 10237,63
6) X32 = 10237,63 + (-50,63) = 10187,00
Якщо до координати останньої точки в полігоні додати приростки на останню лінію, то одержимо координати першої точки. Це і буде контролем вирахування координат.
Ті самі дії з відповідними числами проводимо з координатамиY.
| № точ. | Виміряні кути | По-прав. | Врівноваж. кути | Дирекц. кути, α | Румби, r | Горизонт. прокладання | Обчисленні прирости | Врівноважені прирости | Координати | ||||||
| Δx | попр | Δy | попр | Δx | Δy | X | Y | ||||||||
| 10187,00 | 10200,00 | ||||||||||||||
| 132˚ 24,′4 | ПдСх 47˚ 35,′6 | 203,15 | -136,92 | 150,08 | -136,92 | 150,08 | |||||||||
| 145˚ 42,′4 | + 0,5′ | 145˚ 42,′9 | 10050,08 | 10350,08 | |||||||||||
| 98 ˚05,′3 | ПнСх 98˚ 05,′3 | 176,78 | -24,87 | 172,02 | -0,01 | -24,87 | 175,01 | ||||||||
| 157˚ 50,′0 | + 0,5′ | 157˚ 50,′5 | 10025,21 | 10525,09 | |||||||||||
| 75˚ 55,′8 | ПнЗх 75˚ 55,′8 | 103,08 | 25,06 | -0,01 | -0,01 | 25,05 | 99,99 | ||||||||
| 82˚ 59,′9 | + 0,5′ | 82˚ 60,′4 | 10050,26 | 10625,08 | |||||||||||
| 338˚ 56,′2 | ПнЗх 21˚ 03,′8 | 174,10 | 167,47 | -62,57 | -0,01 | 162,47 | -62,58 | ||||||||
| 119˚ 9,′1 | + 0,5′ | 119˚ 9,′6 | 10212,73 | 10562,50 | |||||||||||
| 278˚ 05,′8 | ПнЗх 81˚ 54,′5 | 176,78 | 24,9 | -175,02 | -0,01 | 24,9 | -175,03 | ||||||||
| 156˚ 46,′8 | + 0,5′ | 156˚ 47,′3 | 10237,63 | 10387,47 | |||||||||||
| 254˚ 53,′1 | ПдЗх 74˚ 53,′1 | 194,18 | -50,63 | -187,46 | -0,01 | -50,63 | -187,47 | ||||||||
| 57˚ 28,′8 | + 0,5′ | 57˚ 29,′3 | 10187,00 | 10200,00 | |||||||||||
| 132˚ 24,′4 | ПдСх 47˚ 35,′6 | ||||||||||||||
Таблиця 12
