Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом

Через прямую a и не лежащую на ней точку Апроходит плоскость, и притом только одна.

Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.

Если две прямые a и b параллельны, то, как и в планиметрии, пишут a || b . В пространстве прямые могут быть размещены так, что они не пересекаются и не параллельны. Этот случай является особым для стереометрии.

Через точку вне данной прямой можно провести прямую, параллельную данной, и притом

только одну.

Если одна из двух параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.

Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.

Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещиваются.

Параллельность трёх прямых?

Параллельность прямой и плоскости

Скрещивающиеся прямые

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек.

Углы с сонаправленными сторонами

Теорема об углах с сонаправленными сторонами .
Если стороны двух углов соответственно сонаправлены, то такие углы равны!
Док-во:
1) O1B1=ОВ, О1А1=ОА
2) ОВВ1О1 – пар-м (лучи ОВ и О1В1 – сонаправ. По признаку ОВ=О1В1) следует ВВ1=ОО1 и ВВ1 || ОО1
3) ОАА1О1 – пар-м (лучи ОА и О1А1 – сонаправл. По признаку ОА=О1А1) следует ОО1=АА1, ОО1||АА1
4) Из 2) и 3) следует АА1||ВВ1 и АА1=ВВ1 следует ВАА1В1- пар-м следует АВ=А1В1 и АВ||А1В1
5) Из 1) и 4) следует треуг. ОАВ = треуг. О1А1В1 (по трем сторонам) следует угол О= углу О1.

Угол между прямыми

Углом между прямым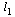и и 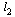называется любой из двух смежных углов, образованных этими прямыми (достаточно определить один из этих углов, так как их сумма равна π)

Параллельные плоскости

Две плоскости называются параллельными, если они не имеют общих точек. (Иногда совпадающие плоскости тоже считают параллельными, что упрощает формулировку некоторых теорем)

Свойства параллельных плоскостей

Свойства

• Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
• Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну
• Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны
• Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

Признак

• Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны