Теорема 3.Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один
Внешний угол треугольника
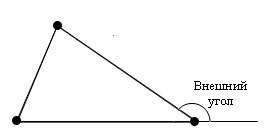
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Окружность
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Прямая, проходящая через две различных точки окружности, называется секущей.
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Касательная к окружности всегда перпендикулярна её радиусу, проведённому в точку касания.
Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
Описанная окружность
Свойства
- Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
- Около любого правильного многоугольника (все углы и стороны равны) можно описать окружность, и притом только одну.
Для треугольника
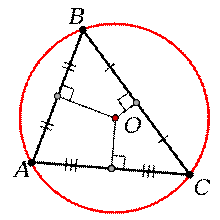
Окружность, описанная около треугольника
- Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
- У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° ( 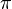 радиан).
радиан).
Можно описать окружность около:
- любого прямоугольника (частный случай квадрат)
- любой равнобедренной трапеции
- любого четырехугольника, у которого сумма противоположных углов равна 180 градусов
Вписанная окружность
Материал из Википедии — свободной энциклопедии

Окружность, вписанная в многоугольник ABCDE
В треугольнике
Свойства вписанной окружности:
- В каждый треугольник можно вписать окружность, притом только одну.
- Центр I вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
В четырёхугольнике
В выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: 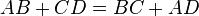 .
.
