Погрешности арифметических действий

Лабораторная робота №1.

Тема:Теория приближенных вычислений.

Цель: сформировать у студентов знания, умения и навыки работы с приближенными числами в применении формул погрешностей элементарных действий и функций, решения обратной задачи теории погрешностей и нахождения значений выражений по способу границ и методом строгого учета абсолютных погрешностей после каждой операции.

Ход работы:

1. Запустите МаthCad.

Абсолютная и относительная погрешности.

2.1. Если х=0,00006, а х^*=0,00005, найти: e_x и d_x.

2.2. Если х=100500, а х^*=100000, найти: e_x и d_x..

2.3. Используя Маthcad найти предельные абсолютные и относительные погрешности чисел х=984,6 и х=2,364, если они имеют только верные цифры: а) в строгом смысле, б) в широком смысле.

2.4. Задано число х = 2,3644 иотносительная погрешность 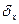=0,07%. Оп­ределить количество верных цифр числа по относительной погрешности.

Решение.

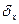= 0,0007 <10^-3, значит, число х имеет по крайней мере, две цифры, вер­ных в строгом смысле. Вычислим:

.

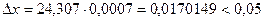То есть, в строгом смысле действительно верны цифры 2 и 3.

2.5. Пусть х =984,6, 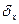=0,008. Определить количество верных цифр в числе х.

Решение.

Очевидно, что 0,008 <0,01= 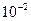. Это означает, что число х имеет, по край­ней мере, одну верную в строгом смысле цифру (цифра 9). Полученный ре­зультат легко подтвердить, используя определение цифры, верной в строгом смысле.

Вычислим 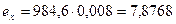. Полученная абсолютная погрешность не превышает половину единицы разряда сотен. Откуда следует, что цифра 9 действительно верна в строгом смысле, как по относительной погрешности, так и по абсолютной.

2.6. Пусть х = 24,307, 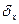= 0,005 %. Определить все верные цифры числа.

Решение.

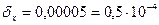, значит, в х, по крайней мере, четыре цифры верны в строгом смысле. Вычислим 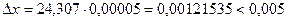. То есть верными цифрами будут являться цифры 2, 4, 3, 0.

2.7. Дано число х = 24,010. Цифры верны в строгом смысле. Указать границы его абсолютной и относительной погрешности.

Решение.

Из определения цифры, верной в строгом смысле, можно заключить, что аб­солютная погрешность числа х не превосходит половины единицы разряда тысячных. Значит е_х =0,0005.

Относительную погрешность найдем по формуле:

.

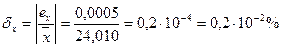2.8. При взвешивании двух грузов получили следующие значения их масс х=0,5 кг, у=50 кг. Считая абсолютную погрешность взвешивания равной 1 г, определить относительную погрешность измерения масс тел х, у. Какое из тел взвешено более точно?

Решение.

Относительную погрешность найдем по формулам:

%

%

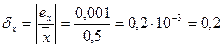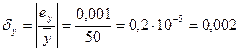Более точно измерен груз весом 50 кг.

Погрешность округленного числа.

3.1. Округляя число х=1,1426 до четырех значащих цифр, определить аб­солютную и относительную погрешности полученных приближений. Цифры верны в широком смысле.

Решение.

Округлим число х до четырех значащих цифр: 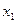=1,143.

По определению верной цифры в широком смысле абсолютная погрешность .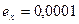

Погрешность округленного числа равна сумме погрешности исходного числа и погрешности округления:

;

;

.

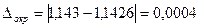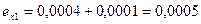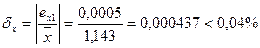3.2. Число х, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата 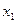вычислить границы абсолютной и относительной погрешностей. В записи числа 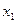указать количество верных цифр по абсолютной и относительной погрешности х=1,1426. Решить в МаthCad.

Решение:

3.3. Со сколькими верными в строгом смысле десятичными знаками после запятой нужно взять:

а) ;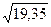

б) sin(0,9);

в) ;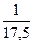

г) 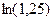, чтобы относительная погрешность не превышала 0,1%.

Решение.

а)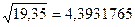

Относительная погрешность 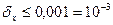. Значит, число 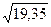, по крайней мере, имеет две верные в строгом смысле цифры.

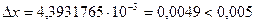. Следовательно, цифры 4 и 3 действи­тельно верны в строгом смысле, поэтому правильный ответ .

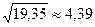б) sin(0,9)=0,7833269;

Относительная погрешность 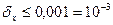. Значит, число sin(0,9), по крайней мере, имеет две верные в строгом смысле цифры.

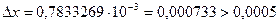. Следовательно, цифры 5, 7 и 3 дей­ствительно верны в строгом смысле, поэтому правильный ответ sin(0,9)=0,783.

в)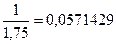

Относительная погрешность 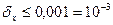. Значит, число, по край­ней мере, имеет две верные в строгом смысле цифры. 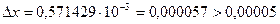. Следовательно, цифры 5 и 7 дей­ствительно верны в строгом смысле, поэтому правильный ответ: 0,057.

г) 1n (1,25) = 0,223144.

Относительная погрешность 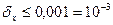. Значит, число 1n (1,25), по крайней мере, имеет две верные в строгом смысле цифры.

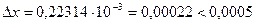. Следовательно, цифры 2, 2, 3, 1 дей­ствительно верны в строгом смысле, поэтому правильный ответ 1n (1,25) = 0,2231. , .

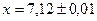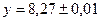Погрешности арифметических действий.

4.1. Найти сумму приближенных чисел, абсолютные погрешности которых даны. В ответе сохранить верные цифры и одну сомнительную.

,

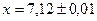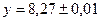
Решение.

Найдем сумму данных чисел х + у = 7,12 + 8,27 = 15,39.

Для определения количества верных цифр найдем абсолютную погреш­ность суммы 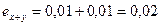, Данное число показывает, что в чис­ле 15,39 верными будут цифры до разряда десятых, т. е. цифры 1, 5 и 3. И т. к. мы отбрасываем число 9, большее пяти, то результат сложения бу­дет 15,4.

По относительной погрешности можно получить более строгую оценку количества верных цифр:

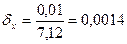и .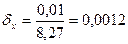

Тогда:

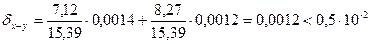
То есть в числе 15,39 цифры 1, 5 верны в строгом смысле.

Ответ:15.

4.2. Найти разность чисел, цифры которых верны в строгом смысле. В ответе сохранить верные цифры и одну сомнительную.

х = 13,876, у = 11,82.

Решение.

Так как цифры данных чисел верны в строгом смысле, то их абсолютные по­грешности не превосходят единицы разряда, в котором записана последняя верная цифра числа. Поэтому , .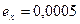

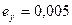Относительная погрешность чисел х и у соответственно равна:

_;

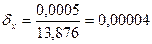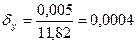
Найдем разность чисел х-у-13,876-11,82 = 2,056.

Найдем абсолютную погрешность полученной разности. Она будет равна:

.

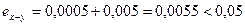То есть в числе 2,056 цифры 2 и 0 верны в строгом смысле.

Найдем относительную погрешность разности. Она будет равна:

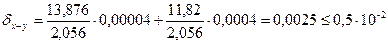
Действительно, две первые цифры верны в числе 2,056.

Ответ:2,06.