Приведение системы сил к заданному центру.

Лекция 3

Краткое содержание: Приведение произвольной и плоской системы сил к центру. Теорема о параллельном переносе силы, основная теорема статики Приведении системы сил к данному центру Главный вектор и главный момент системы сил. Зависимость главного момента от выбора центра. Аналитическое определение главного вектора и главного момента системы сил. Инварианты системы сил. Приведение системы сил к простейшему виду. Частные случаи приведения произвольной системы сил, динамический винт. Теорема Вариньона о моменте равнодействующей.

Приведение силы к заданному центру (Лемма Пуансо)

Равнодействующая системы сходящихся сил непосредственно находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку.

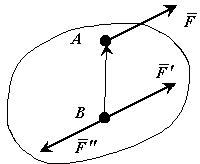
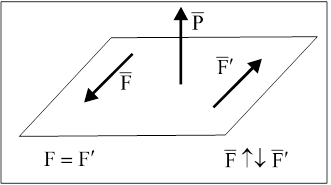
Лемма Пуансо о параллельном переносе силы.. Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Пусть сила 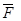приложена в точке A. Действие этой силы не изменяется, если в точке B приложить две уравновешенные силы. Полученная система трех сил представляет собой силу 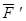равную 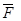, но приложенную в точке В и пару 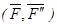с моментом 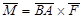. Процесс замены силы 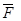силой 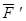и парой сил 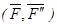называется приведением силы 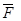к заданному центру В . ■

Приведение системы сил к заданному центру.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил.

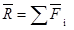
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.

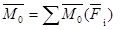
Теорема Пуансо (Основная теорема статики)

Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке (центре приведения), момент пары равен главному

моменту системы сил относительно этой точки.

ДОКАЗАТЕЛЬСТВО.

Точка О — центр приведения. По лемме Пуансо перенесем силу F1 в точку О. При этом вместо F1 имеем в точке О такую же силу F1’ и дополнительно пару сил с моментом m1.

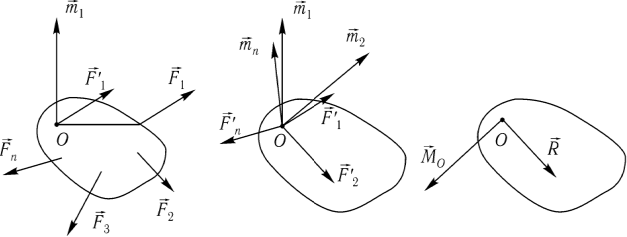
Аналогично перенесем все остальные силы. В результате получим систему сходящихся сил и систему пар сил. По теореме о существовании равнодействующей системы сходящихся

сил их можно заменить одной силой R, равной главному вектору. Систему пар по теореме о сложении пар можно заменить одной парой, момент которой равен главному моменту Mo. ■

Инварианты статики

Инварианты статики — характеристики системы сил, не зависящие от выбора центра приведения.

Первый инвариантстатики — главный вектор системы сил (по определению).

Второй инвариантстатики — скалярное произведение главного вектора и главного момента.

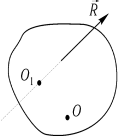
В самом деле, главный момент, очевидно, зависит от выбора центра приведения. Рассмотрим произвольную систему сил 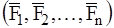. Приведем ее сначала к центру О, а затем к центру О₁ .

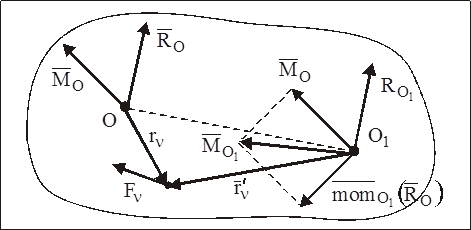
Из рисунка видно ,что 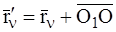.Поэтому формула для 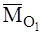примет вид

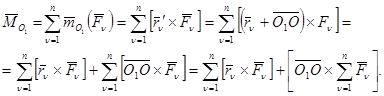
Или .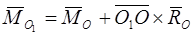

Домножим обе части этого равенства на 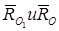соответственно, учитывая что главный вектор системы сил является первым инвариантом статики: 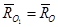. По

свойству смешанного произведения векторов 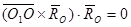, следовательно:

.

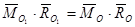Если воспользоваться определением скалярного произведения, то для второго инварианта можно получить еще одну форму:

.

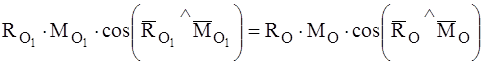Так как 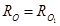, то предыдущее выражение примет вид:

.

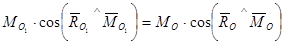Таким образом, проекция главного момента на направление главного вектора есть величина постоянная для данной системы сил и не зависит от выбора центра приведения.

Частные случаи приведения произвольной системы сил к простейшему виду

1) Если при приведении системы сил к центру О 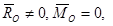то на основании (6.4) можно записать

.

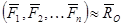В этом случае система сил приводится к равнодействующей, приложенной в центре приведения и совпадающей по величине и направлению с главным вектором.

2)Если при приведении системы сил к центру О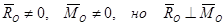

то представив 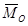в виде пары сил 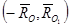с плечом ,

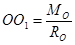получим: .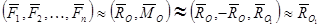

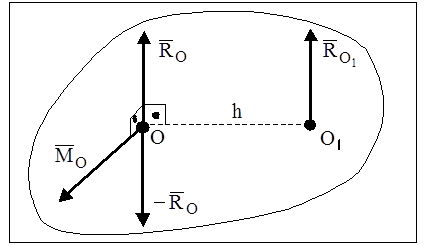
В этом случае система сил приводится к равнодействующей, совпадающей по величине и направлению с главным вектором, а линия действия равнодействующей отстоит от линии действия главного вектора на расстоянии .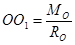

3)Если при приведении системы сил к центру О 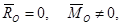то можно записать

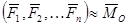,то есть система сил приводится к паре сил с моментом, равным главному моменту системы сил.

4)Если при приведении системы сил к центру О 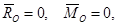то можно записать

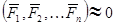, т.е. система сил находится в равновесии.

4)

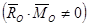
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом.

Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме.

Разложив 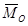на две составляющие 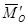- вдоль главного вектора и 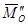- перпендикулярно главному вектору, для 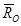и 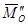будем иметь случай 2),а вектор 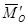, как свободный можно перенести параллельно самому себе в точку О₁:

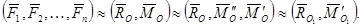
Вектора 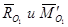представляют собой динаму, где , .

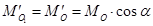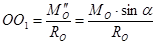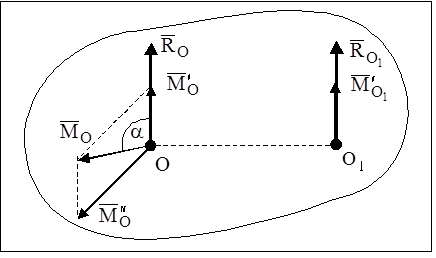
В рассматриваемом случае приведения системы сил главный момент 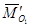имеет минимальное значение. Это значение момента сохраняется при приведении заданной системы сил к любой точке, лежащей на линии действия главного вектора 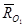и главного момента 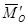. Уравнение этой линии( центральная винтовая ось системы сил) определяется из условия коллинеарности векторов 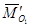и : .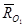

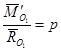С учетом , ,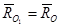

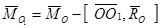уравнение центральной оси в векторной форме можно записать так:

.

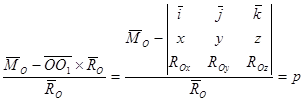Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:

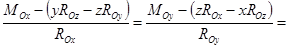
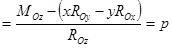
Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.

Теорема Вариньона.

Если система сил имеет равнодействующую, то ее момент относительно любого центра равен сумме моментов всех сил системы относительно того же центра.

ДОКАЗАТЕЛЬСТВО.

Пусть 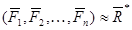, а 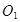— точка на линии действия равнодействующей. Как было доказано: ,

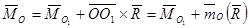но 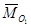= 0, следовательно, ■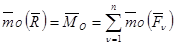