Определение равнодействующей системы сил аналитическим способом

Практическая работа 1

Тема: Определение реакций связей аналитическим и графическим способами.

Цель: Изучить виды связей, научиться определять их реакции.

Теоретическая часть:

Тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным.

Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным.

Все то, что ограничивает перемещения данного тела в пространстве, называется связью.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или реакцией связи.

Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.

Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.

Все виды связей можно разделить на несколько типов.

1. Связь – гладкая опора (без трения).

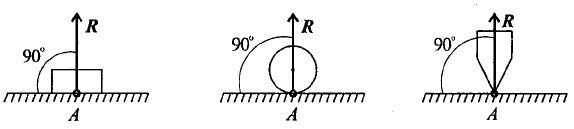
Рисунок 1.1

Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рисунок 1.1).

2. Гибкая связь (нить, веревка, трос, цепь).

Реакция нити направлена вдоль нить от тела, при этом нить может быть только растянута (рисунок 1.2).

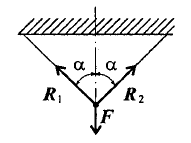
Рисунок 1.2

3. Жесткий стержень.

Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи (рисунок 1.3).

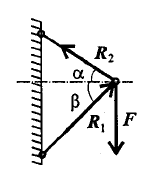
Рисунок 1.3

4. Шарнирная опора.

Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир. Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности

(рисунок 1.4).

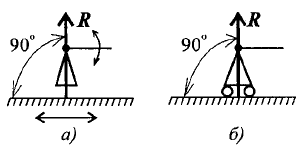
Рисунок 1.4

Неподвижный шарнир. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать в виде двух составляющих: горизонтальной и вертикальной (рисунок 1.5).

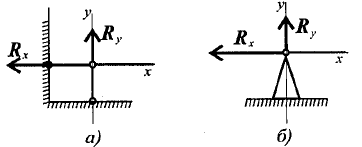
Рисунок 1.5

5. Защемление или «заделка».

Любые перемещения точки крепления невозможны.

Реактивную силу принято представлять в виде двух составляющих вдоль осей координат (рисунок 1.6).

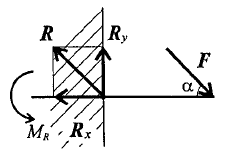
Рисунок 1.6

Пример.

Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рисунок 1.7).

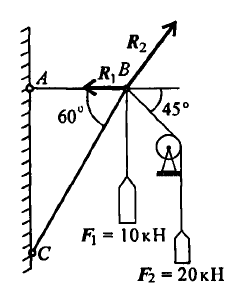
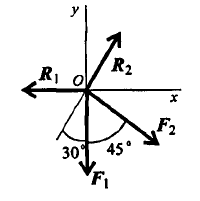
Рисунок 1.7

1. Аналитический способ.

1. Определяем вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ – тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу – реакция направлена в верх.

2. Освобождаем точку В от связи.

3. Выберем направление осей координат, ось Ох совпадает с реакцией .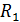

4. Запишем уравнения равновесия точки В:

;

.

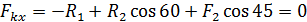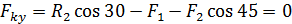5. Из второго уравнения получаем:

.

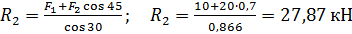Из первого уравнения получаем:

.

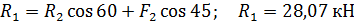2. Графический способ.

1. Выбираем масштабный коэффициент сил: µ = 1 Н/мм

Определяем отрезки, изображающие силы 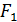и :

,

.

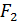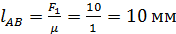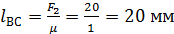2. Полученная система сил находится в равновесии, поэтому силовой

многоугольник должен быть замкнутым (рисунок 1.8).

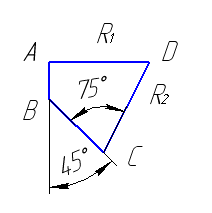
Рисунок 1.8

3. Вычисляем реакци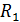и и 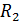, полученные в результате графического

решения:

,

.

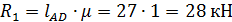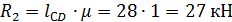Вычисляем погрешности:

.

;

.

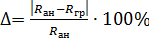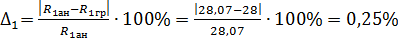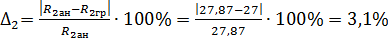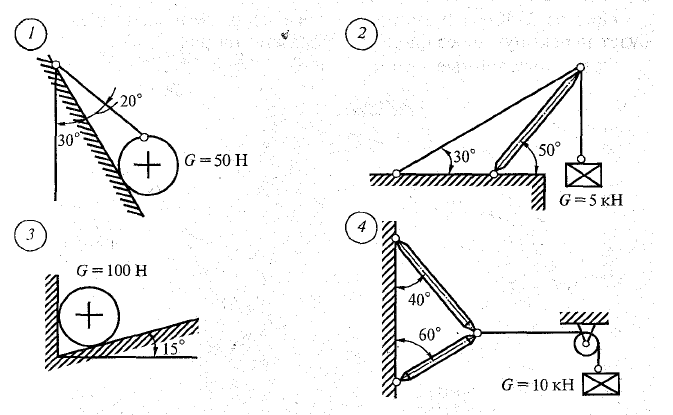
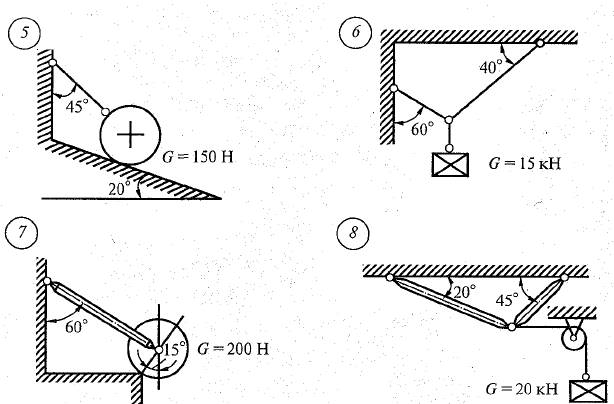
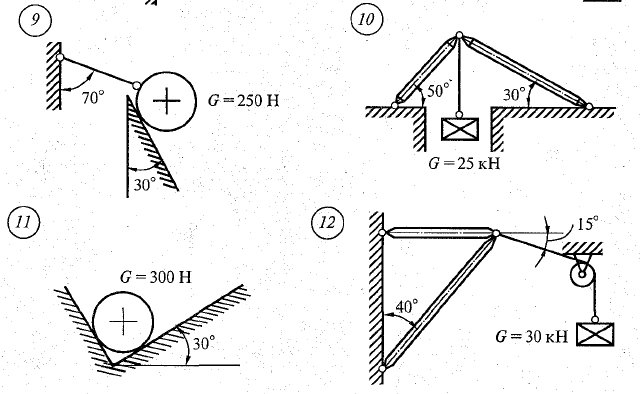
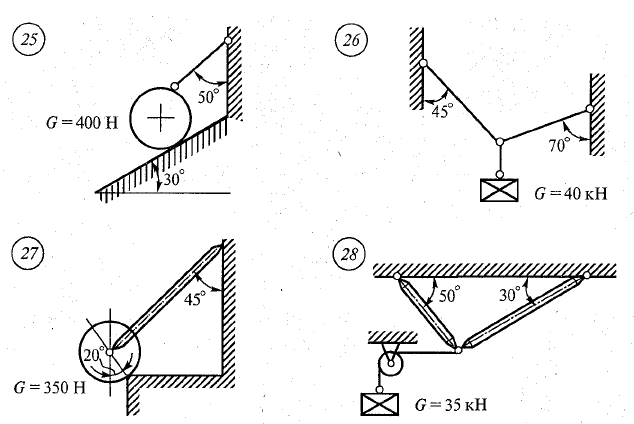
Задание.

Аналитически и графически определить реакции связей, сравнить результаты.

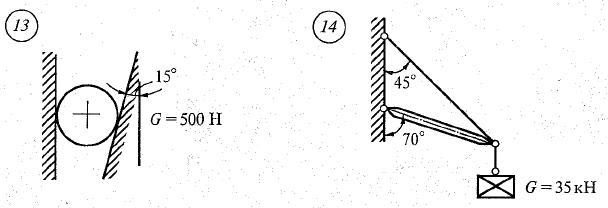
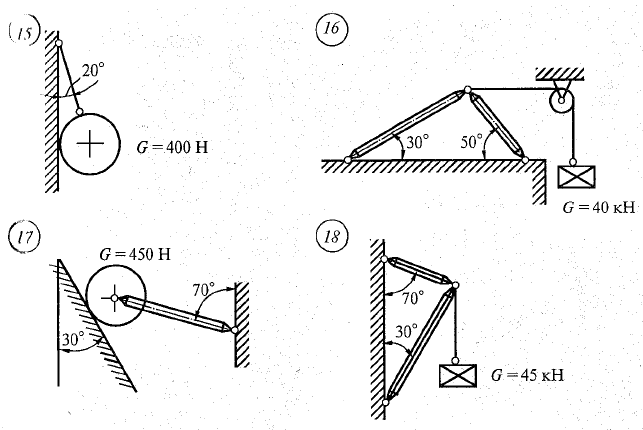
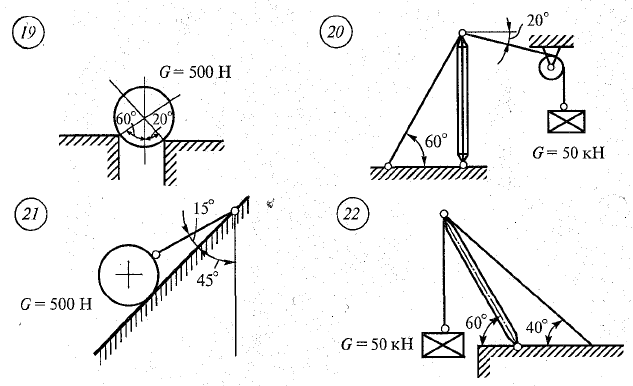
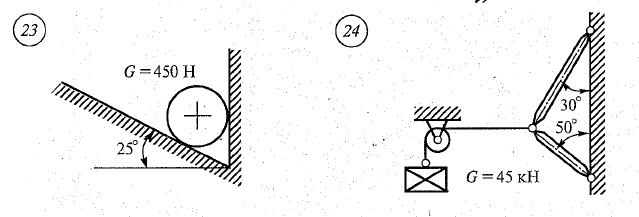
Контрольные вопросы.

1. Что называется связью?

2. Перечислите основные виды опор.

3. Запишите аксиому связей.

4. Как направлена реакция гибкой нити?

Содержание отчета

1. Схема фигуры в масштабе

2. Решение

3. Ответы на контрольные вопросы

4. Вывод.

Практическая работа № 2

Тема:Определение реакций опор двух опорной балки.

Цель работы:Научится определять реакции опор балки установленной на двух опорах.

Теоретическая часть:

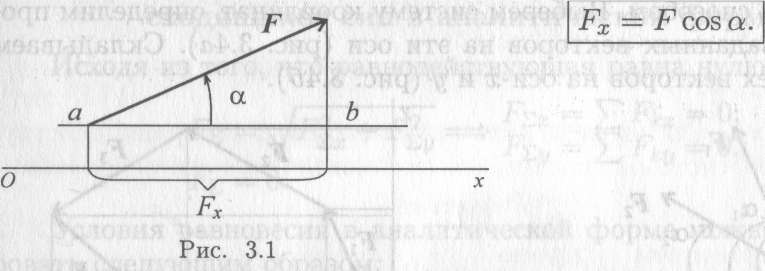
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

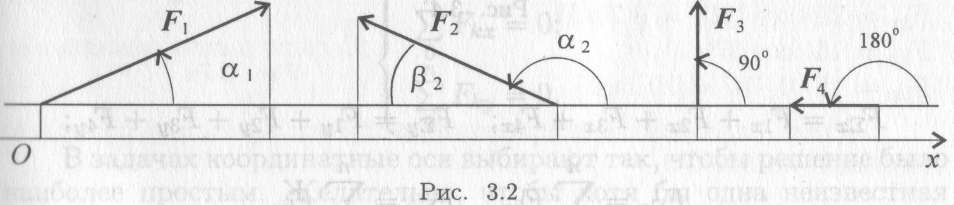
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

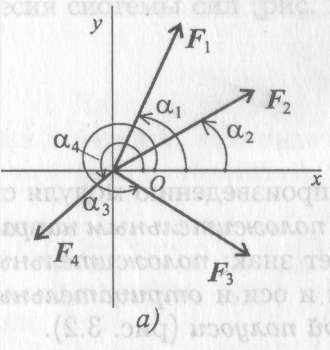
F_1x = F₁ cos α₁>0; F_2x = F₂cos α₂= - F₂ cos β₂;

cos α₂ = cos (180° — β₂)= — cos β₂

F_3x = F₃ cos90° = 0; F_4x = F₄ cos180° = - F₄.

Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

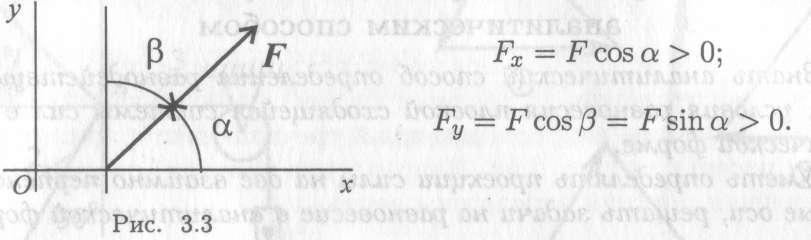
Определение равнодействующей системы сил аналитическим способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом.

Выберем систему координат, определим пропорции всех заданных векторов на эти оси (рис. 3.4, а).

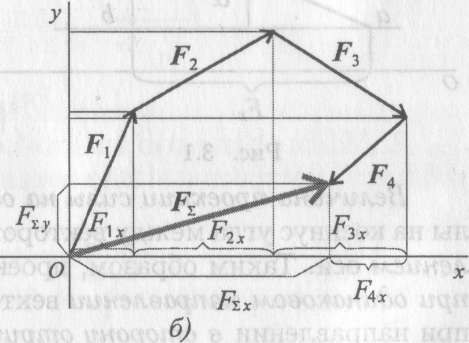
Складываем проекции всех векторов на оси х и у (рис. 3.4, б).

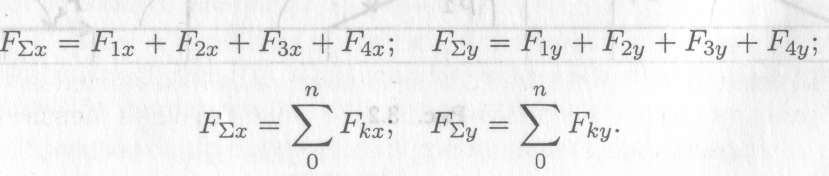
Рис. 3.4

Модуль (величину) равнодействующей можно найти по известным проекциям:

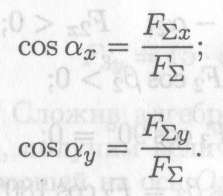
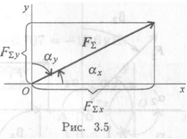
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).