Решение неоднородных задач для уравнения теплопроводности

Рассмотрим несколько конкретных задач.

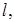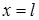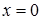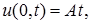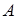Задача 1.(Задан режим на концах). Дан тонкий однородный стержень длиной начальная температура которого равна нулю. Источники тепла отсутствуют. На конце температура поддерживается равной нулю, а на конце она растет линейно со временем, так что где – постоянная. Найти распределение температуры вдоль стержня при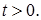

Решение.Искомая функция 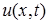есть решение задачи

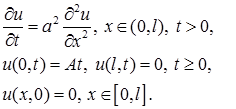
Сначала (правило 1) строим вспомогательную функцию 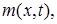удовлетворяющую краевым условиям. В простейшем случае это линейная функция, проходящая через точк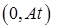и и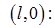

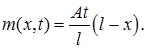
Функцию 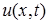представляем в виде суммы:

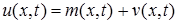
Для новой неизвестной функции 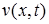получаем задачу

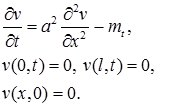
Неоднородность переведена из краевых условий в уравнение. Здесь 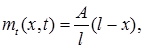то есть неоднородность не зависит от 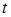(стационарна).

Решение задачи со стационарной неоднородностью в уравнении ищем в виде суммы (см. ч. III, п.7)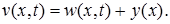

Здесь функция 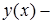решение краевой задачи для обыкновенного дифференциального уравнения

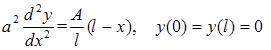
Интегрируя дважды, находим общее решение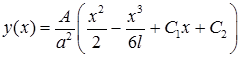

Из краевых условий определяем 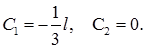Значит,

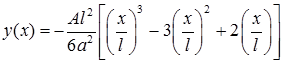
Для функции 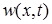получаем задачу

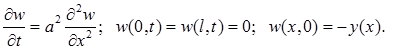
Эта задача в предыдущем пункте решена методом Фурье:

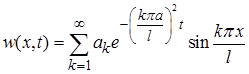
Здесь 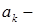коэффициент Фурье разложения функции 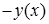по синусам::

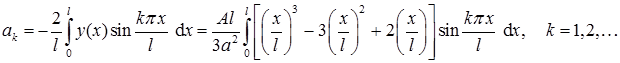
Вычислим интеграл по частям, при этом не следует представлять интеграл в виде суммы, чтобы не увеличивать объём работы.

Получим 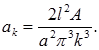Значит,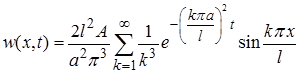

Осталось сложить найденные функции :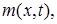

●

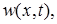
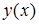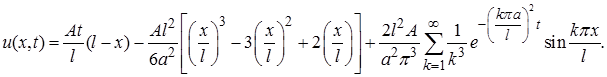Задача 2. (Задан режим на одном конце стержня и теплообмен на другом).

Дан тонкий однородный стержень длиной 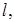боковая поверхность которого теплоизолирована. Начальная температура стержня известна. Конец стержня 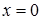поддерживается при температуре, равной нулю. На конце 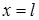происходит теплообмен с окружающей средой, температура которой считается равной нулю. Определить температуру стержня при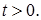

Решение. Требуется решить задачу:

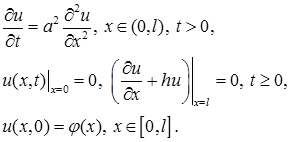
Ищем решение в виде произведения 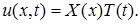Из соотношения

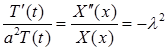
получаем задачу Штурма – Лиувилля для функции :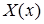

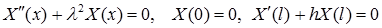(1)

Общее решение уравнения имеет вид 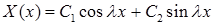. Первое граничное условие (на левом конце) дает 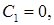второе условие (на правом конце) приводит к трансцендентному относительно собственных значений уравнению 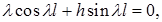откуда 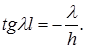Обозначим 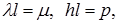и решим уравнение 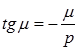графически:

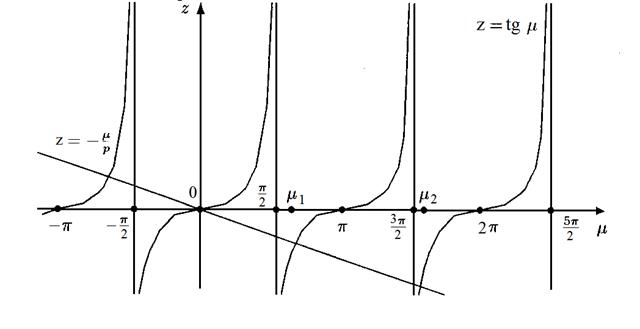
Пусть 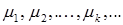– положительные корни этого уравнения (отрицательные корни можно не рассматривать, относя знак 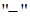к произвольной постоянной). Функции

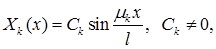
являются собственными функциями задачи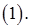

Функции 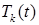определяем из уравнения

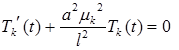
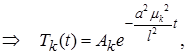
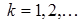
Строим ряд

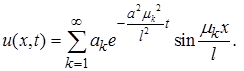(2)

Постоянные 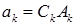подберем так, чтобы удовлетворить начальному условию задачи

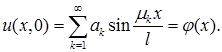(3)

Заметим, что функции 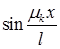не являются 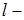периодическими, поэтому это равенство нельзя рассматривать, как разложение начальной функции 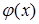в тригонометрический ряд Фурье по синусам на .

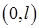Умножим обе части соотношения (3) на 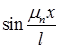и проинтегрируем в пределах от 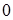до :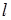

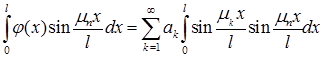
Но собственные функции ортогональны, т.е. 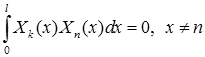. Поэтому справа сохраняется только слагаемое, соответствующее значению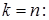

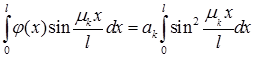(4)

Подсчитаем интеграл, стоящий справа в (4):

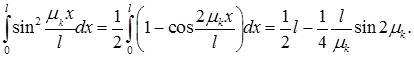
Вспоминая, что 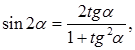и заменяя 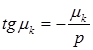, получим

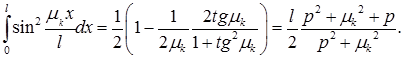
Теперь из соотношения (4) можем найти :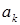

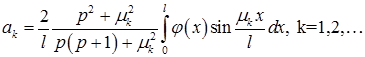
Замечание. Можно было для вычисления коэффициентов 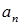воспользоваться свойством 5 собственных функций (см. раздел III, п.1в)

, ,

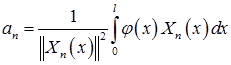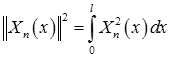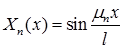
Осталось подставить найденные коэффициенты 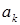в ряд (3):

●

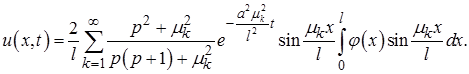Задача 3. Найти температуру стрежня 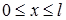с теплоизолированной боковой поверхностью. На концах стержня происходит теплообмен по закону Ньютона со внешней средой, имеющей постоянную температуру 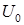. Начальная температура произвольна.

Решение.Рассматривается задача

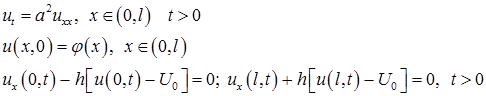
Решение ищем в виде

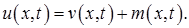
Функция 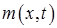должна удовлетворять неоднородным граничным условиям. Легко убедиться, что можно положить .

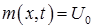Функция 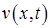удовлетворяет однородному уравнению

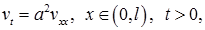
однородным граничным условиям

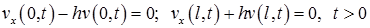
и начальному условию

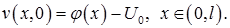
В соответствии с методом Фурье

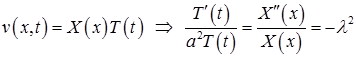
Получаем 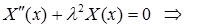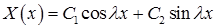. Вычислим

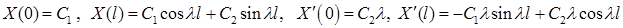
Первое граничное условие дает

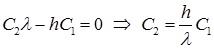
Второе граничное условие принимает вид

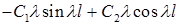
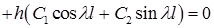
Так как 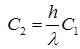, то из второго граничного условия получаем

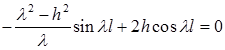
Собственные значения 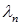находим из трансцендентного уравнения

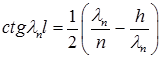(5)

Обозначим положительные корни этого уравнения 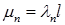. Тогда собственные функции 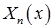имеют вид

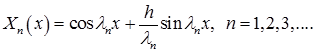
Находим соответствующие функции .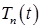

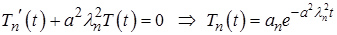
Значит, функция 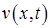представляется рядом:

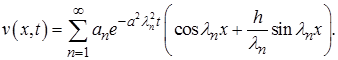
Осталось постоянные 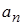определить из начального условия. При

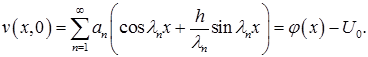
Начальную функцию 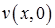надо разложить в ряд Фурье по ортогональным на 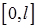собственным функциям :

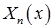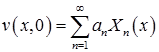
Коэффициенты разложения определяются по формуле

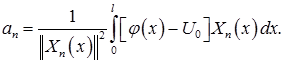
Находим квадрат нормы собственных функций:

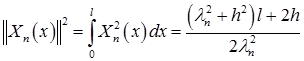
Здесь интеграл 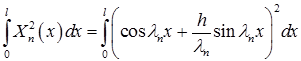вычисляется непосредственно, затем полученные 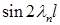и 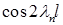выражаются через 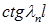из соотношения (5). ●

Задача 4. Найти температуру стержня 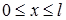, на боковой поверхности которого происходит теплообмен по закону Ньютона со средой, температура которой 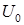. Начальная температура произвольна. На концах стержня поддерживается постоянная температура.

Решение. Рассматривается задача:

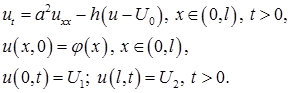
Представим функцию 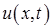в виде суммы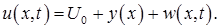

Найдем 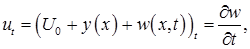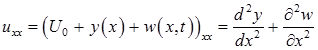и подставим в уравнение:

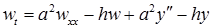
Начальное и граничные условия принимают вид:

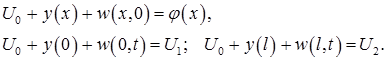
Значит, можно полагать, что функция 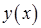есть решение задачи

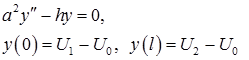(6)

Тогда функция 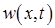есть решение задачи

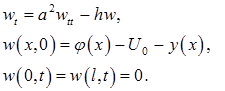(7)

Найдем функцию 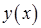– решение краевой задачи (6). Корни характеристического уравнения 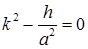суть .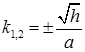

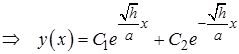Постоянные 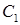и 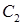определим из граничных условий:

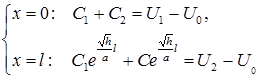
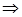
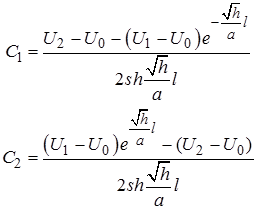
Получили решение задачи (6):

.

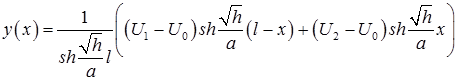Задачу (7) решаем методом Фурье:

,

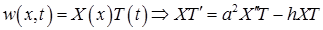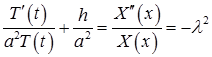
Значит, ,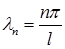

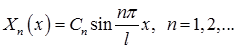
Соответствующие функции 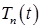находим из уравнения

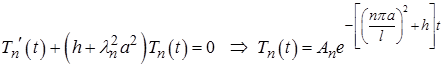
Для функции 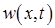запишем ряд

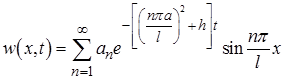
Из начального условия определяем коэффициенты :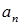

●
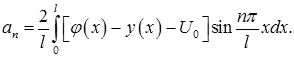