Среднее время пребывания заявки в очереди системы равно среднему числу заявок в очереди системы, делённому на интенсивность потока заявок

Простейшие системы массового обслуживания и их характеристики.

1. n - канальная СМО с отказами ( задача Эрланга ).

Рассмотрим одну из первых по времени классических задач теории массового обслуживания. Эта задача возникла из практических нужд телефонии и была решена в начале прошлого века датским математиком Эрлангом. Задача ставится так:

Имеется n каналов (линий связи), на которые поступает поток заявок с интенсивностью . Поток обслуживаний имеет интенсивность (величина, обратная среднему времени обслуживания ).

Найти предельные вероятности состояний СМО, а также характеристики её эффективности.

Характеристики эффективности СМО:

А –абсолютная пропускная способность, то есть среднее число заявок, обслуживаемых в единицу времени.

Q –относительная пропускная способность, то есть вероятность обслуживания поступившей заявки.

P_отк -вероятность отказа, то есть вероятность того, что поступившая заявка не будет обслужена.

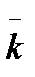- среднее число занятых каналов.

Пока остановимся на этих характеристиках, так как выбор показателей эффективности зависит от типа СМО.

Решение задачи Эрланга. Состояние системы S (СМО) будем нумеровать по числу заявок, находящихся в системе ( в данном случае оно совпадает с числом занятых каналов ).

S₀ – в СМО нет ни одной заявки;

S₁ – в СМО один канал занят, остальные свободны;

S₂ – в СМО два канала заняты, остальные свободны;

…………………………………………………………..

S_j – в СМОj- каналов заняты, остальные свободны;

………………………………………………………….

S_n – в СМО все n каналов заняты.

Систему массового обслуживания хорошо иллюстрирует граф состояний

Разметим этот граф – проставим у стрелок интенсивности потоков событий. Из S₀ в S₁ систему переводит поток заявок с интенсивностью 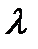( как только приходит заявка, система перескакивает из S₀ вS₁). Аналогично, из S₁ в S₂ и так далее. Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии S₁ (работает один канал). Он производит 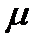обслуживаний в единицу времени. Проставляем у стрелки S₁ 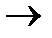S₀ интенсивность 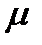. Пусть система находится в состоянии S₂ (работают два канала). Чтобы система могла перейти в состояние S₁ нужно, чтобы либо закончил обслуживание первый канал, либо – второй; суммарная интенсивность двух каналов обслуживаний равна 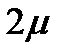. Суммарный поток обслуживаний, создаваемый тремя каналами имеет интенсивность 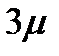, j каналами - 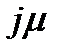и так далее.

Граф состояний СМО соответствует схеме гибели и размножения.

Предельные вероятности в схеме гибели и размножения имеют вид:

.

, , , ,

.

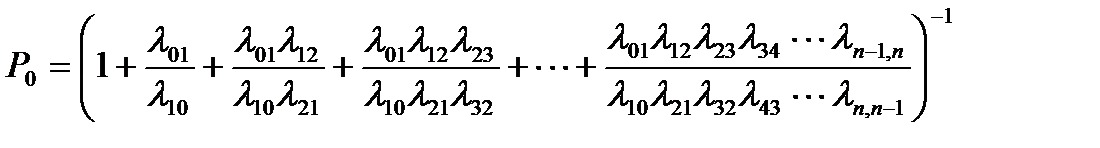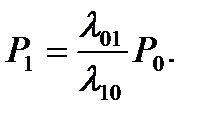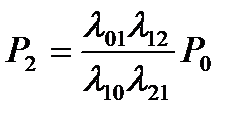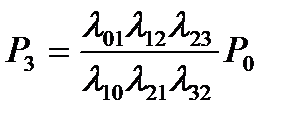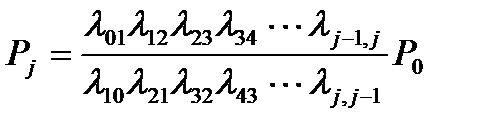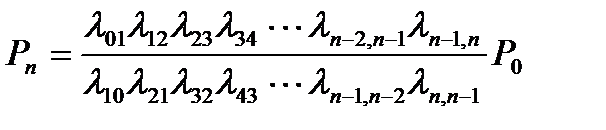Зная потоки интенсивностей в СМО, воспользуемся готовыми формулами для предельных вероятностей в схеме гибели и размножения, получим

;

; ; ; … ; … .

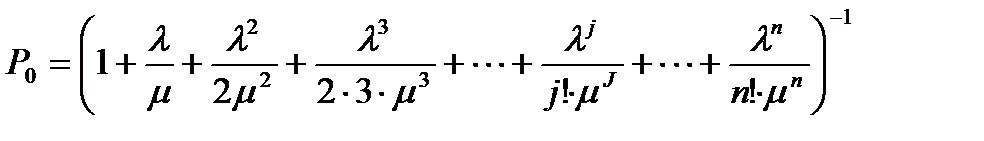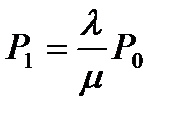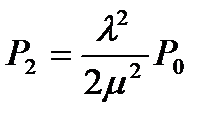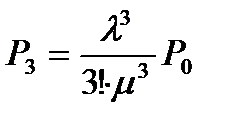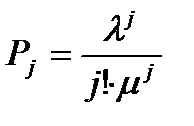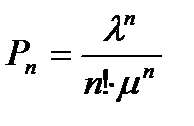Обозначим 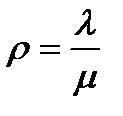. Будем называть 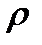- коэффициентом загрузки системы,

её смысл – среднее число заявок, приходящие за среднее время обслуживания одной заявки ( интенсивность нагрузки канала ).

Пользуясь этим обозначением, перепишем формулы в виде:

, ,

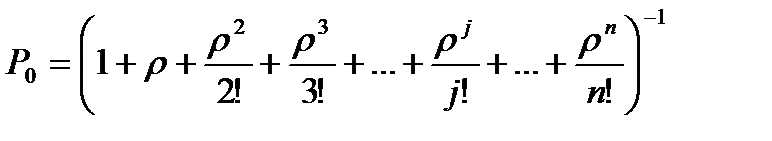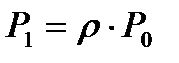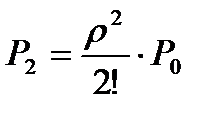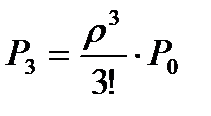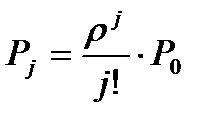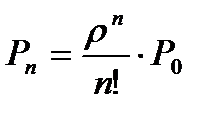, , … , … . ( 1.1 )

Эти формулы называются формулами Эрланга – в честь основателя теории массового обслуживания.

Теперь можно вычислять характеристики эффективности СМО. Сначала найдём 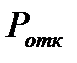- вероятность того, что пришедшая заявка получит отказ. Для этого нужно, чтобы все n каналов были заняты, значит

.

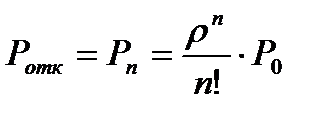Теперь находим относительную пропускную способность – вероятность того, что заявка будет обслужена

.

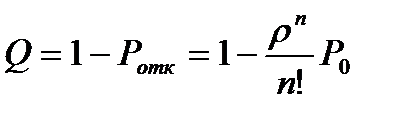Абсолютную пропускную способность получим, умножая интенсивность потока заявок 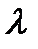на Q

.

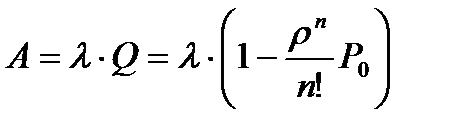Осталось определить среднее число занятых каналов 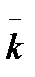. Эту величину можно определить как математическое ожидание дискретной случайной величины с возможными значениями 0, 1, 2, 3,…,nи вероятностями этих значений P₀, P₁, P₂, P₃,…, P_n.

.

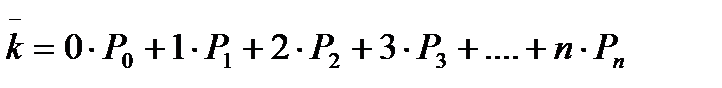Если подставить сюда формулы Эрланга, то получим сложное выражение, которое потребует громоздких преобразований. Откажемся от этого пути. сделаем по другому.

Нам известна величина А –абсолютная пропускная способность, то есть среднее число заявок, обслуживаемых в единицу времени. Каждый занятый канал в единицу времени обслуживает в среднем 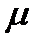заявок. Следовательно, среднее число занятых каналов равно

.

__________________________________________________________________

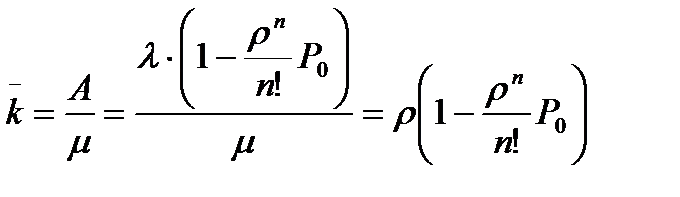Пример №3 .АТС имеет k=5 линий связи. Поток вызовов простейший с интенсивностью 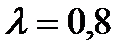вызовов в минуту. Среднее время переговоров составляет τ=3 минуты. Время переговоров распределено по показательному закону. Найти: а)вероятность того, что все линии связи заняты (вероятность отказа); б) абсолютную и относительную пропускные способности АТС; в) среднее число занятых линий связи. Определить сколько линий связи должна иметь АТС (оптимальное число линий связи), чтобы вероятность отказа не превышала 0,01?

Решение.Будем нумеровать состояния АТС по числу занятых линий связи: S₀ – все линии свободны, S₁ – одна линия занята, остальные свободны; S₂ – две линии заняты, остальные свободны;…… S₅ – все пять линий заняты.

В данном примере мы имеем дело с многоканальной СМО ( n=5 ) c отказами, так как если все пять линий связи заняты, то заявка получит отказ.

Находим интенсивность потока обслуживания 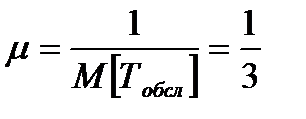разговора в минуту. Коэффициент загрузки СМО составляет

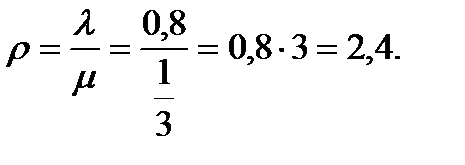По формулам Эрланга вычисляем:

, .

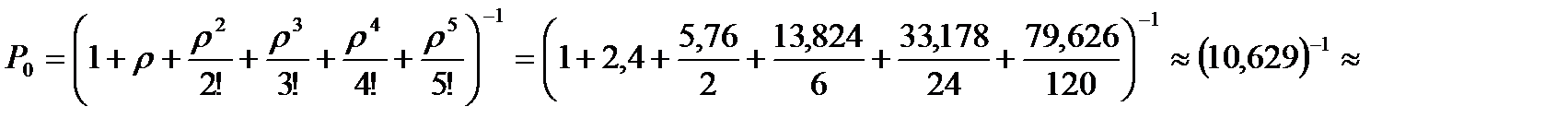
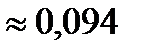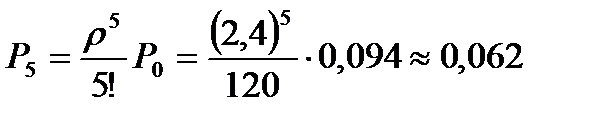Вероятность отказа 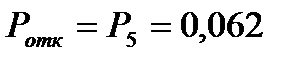. Находим относительную пропускную способность 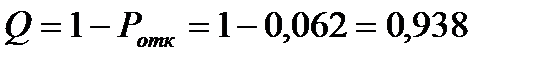. Это вероятность того, что вновь поступившая заявка будет обслужена. Вычислим абсолютную пропускную способность системы 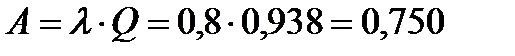, следовательно, система обслуживает в среднем 0,75 заявки в минуту. Теперь вычислим средне число занятых каналов 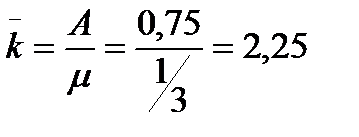, следовательно, АТС в среднем имеет половину линий связи постоянно занятыми.

Поскольку вероятность отказа Р_отк=0,062 превышает 0,01, то число линий связи следует увеличить. Допустим, что линий связи стало n=6. Тогда пересчитаем Р₀:

.

, .

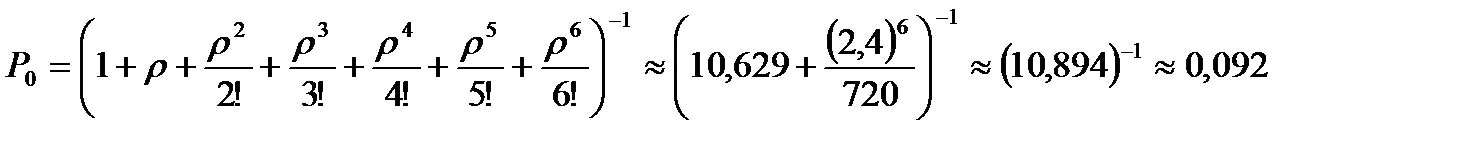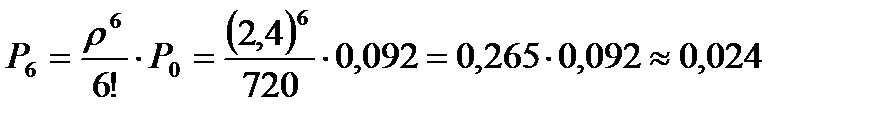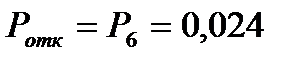При n=6вероятность отказа 0,024 превышает 0,01. Значит, число линий надо увеличить. При n=7 получим

,

, ,

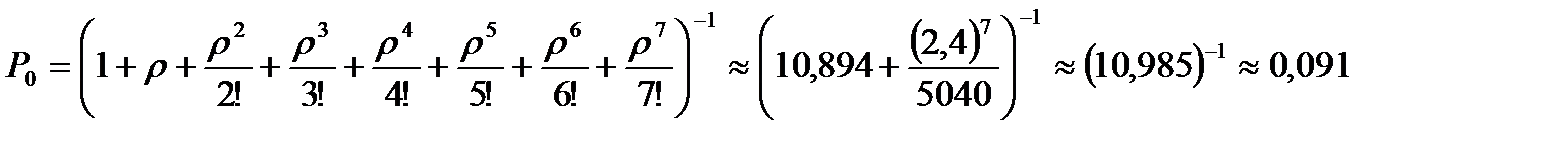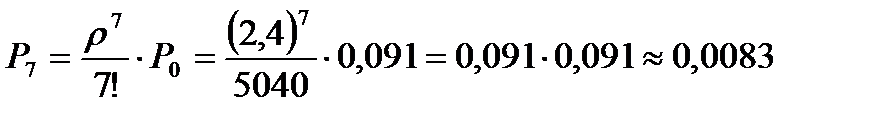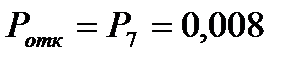следовательно, при n=7 вероятность отказа не превышает 0,01.

Таким образом, для обеспечения требуемой вероятности отказов следует увеличить количество линий связи АТС до 7.

Пример №3 решен.

2. Одноканальная СМО с неограниченной очередью.

Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений. Поступает поток заявок с интенсивностью 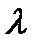, поток обслуживаний имеет интенсивность 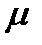. Требуется найти предельные вероятности состояний СМО, а также характеристики её эффективности:

L_сист – среднее число заявок в системе;

W_сист – среднее время пребывания заявки в системе;

L_оч - среднее число заявок в очереди;

W_оч - среднее время пребывания заявки в очереди;

P_зан - вероятность того, что канал занят ( степень загрузки канала ).

Решение.Состояния системы, как и раньше, будем нумеровать по числу заявок в системе:

S₀ – в СМО канал свободен;

S₁ – в СМО канал занят, очереди нет;

S₂ – в СМО канал занят, одна заявка в очереди;

…………………………………………………………..

S_j – в СМОканал занят, ( j-1 ) заявок в очереди;

………………………………………………………….

Теоретически число состояний системы ничем не ограничено. Граф состояний имеет вид

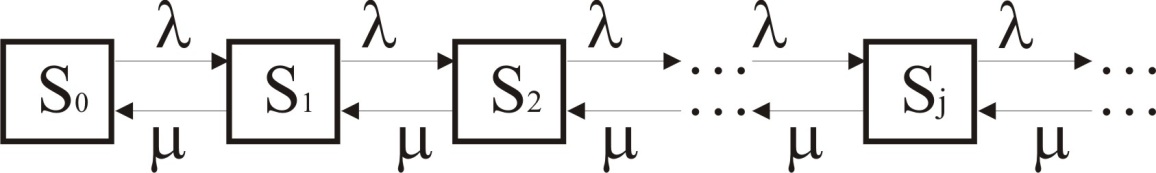
Существуют ли в этом случае финальные вероятности? Предельные вероятности существуют не всегда, только тогда, когда система не перегружена. Посчитаем предельные вероятности системы по формулам схемы гибели и размножения

.

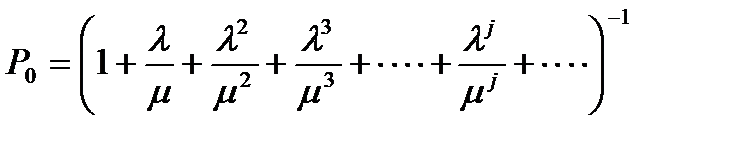В нашем случае число слагаемых будет бесконечным. В скобках стоит геометрическая прогрессия. Только бесконечно убывающая геометрическая прогрессия имеет конечную сумму. Если ввести коэффициент загрузки системы 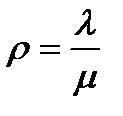,то

.

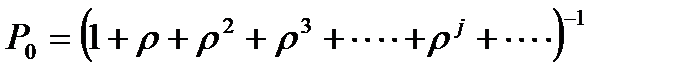В случае 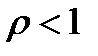имеем .

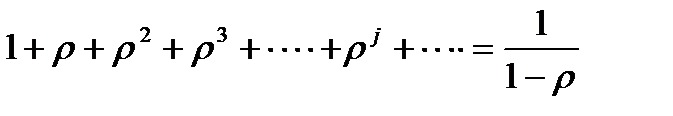Откуда сразу следует, что

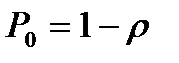. (2.1)

Вероятности P₁, P₂, P₃,...., P_j,…найдутся по формулам:

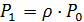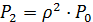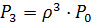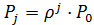; ; ; ; ;…(2.2)

Эти вероятности образуют геометрическую прогрессию, с другой стороны должно выполняться равенство:

.

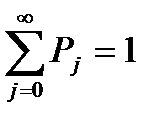Найдём среднее число заявок L_сист в СМО. Случайная величина Z – число заявок в системе – имеет возможные значения: 0, 1, 2, 3,….,.j…. с вероятностями: Р₀, Р₁, Р₂, Р₃, ….., Р_j,….

.

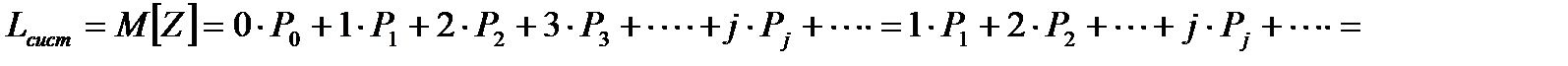
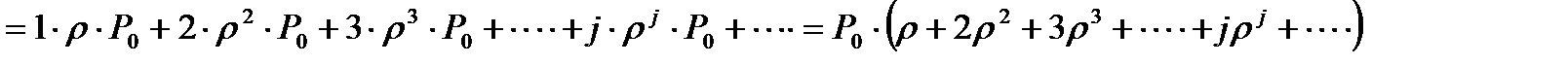Можно записать коротко

.

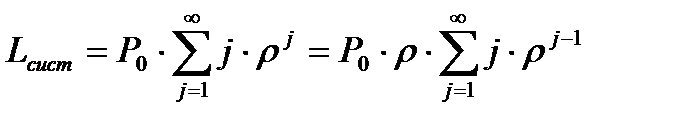Представим 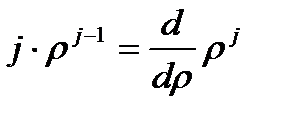, тогда

.

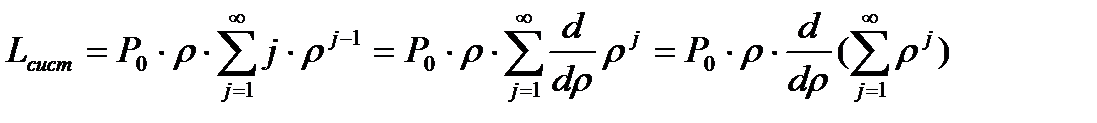Вычислим сумму бесконечно убывающей геометрической прогрессии

,

.

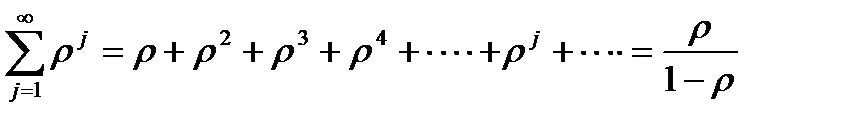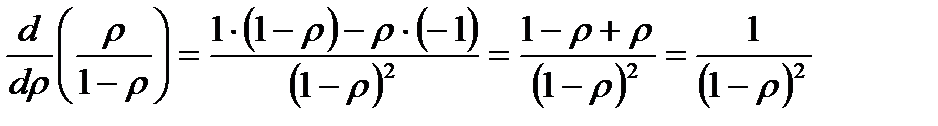Теперь можно получить окончательное выражение для

.

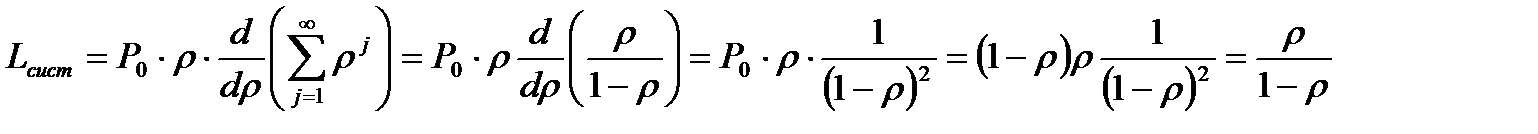Итак, среднее число заявок в СМО вычисляется по формуле

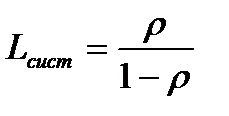. (2.3)

Применим формулу Литтла и найдем среднее время пребывания заявки в системе

.

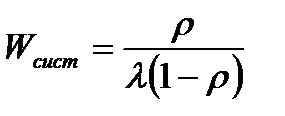Теперь вычислим среднее число заявок в очереди. Очевидно, среднее число заявок в очереди L_оч равно среднему числу заявок в системе L_сист минус L_обсл -среднее число заявок, находящихся под обслуживанием.

Число заявок под обслуживанием является случайной величиной, которая может принимать два значения: либо нуль, либо единица. Математическое ожидание такой величины равно

.

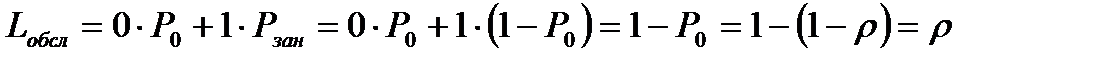Итак, среднее число заявок, находящихся под обслуживанием, равно

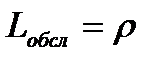. (2.4)

Тогда 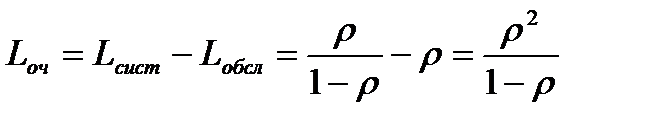. Среднее число заявок в очереди равно

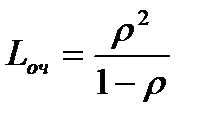. (2.5)

По формуле Литтла вычислим среднее время пребывания заявки в очереди

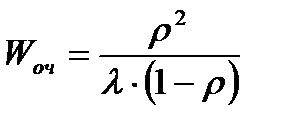. (2.6)

Пример №4Железнодорожная сортировочная горка, на которую подается простейший поток составов с интенсивностью 𝞴=3 состава в час, представляет собой одноканальную СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со средним значением τ=15 минут.

Найти: а) предельные вероятности состояний СМО;

б) среднее число составов, связанных с горкой;

в) среднее число составов в очереди;

г) среднее время пребывания состава в СМО;

д) среднее время пребывания состава в очереди.

Решение.

Железнодорожную сортировочную горку будем рассматривать как одноканальную СМО с неограниченной очередью. Интенсивность потока поездов 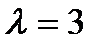состава в час. По условию время обслуживания одного состава на горке занимает в среднем τ=15 минут, то есть 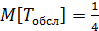часа.

Интенсивность потока обслуживаний 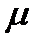вычислим 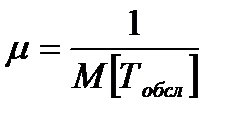= 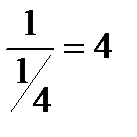состава в час.

а) Предельные вероятности существуют только тогда, когда система не перегружена, то есть когда коэффициент загрузки системы 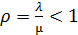. В данной задаче 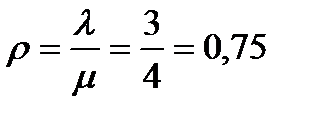<1, следовательно, предельные вероятности состояний системы существуют.

Состояния системы будем нумеровать по числу составов, поступающих на горку:

S₀ – горка свободена;

S₁ – горка занята, очереди нет;

S₂ – горка занята, один состав в очереди;

…………………………………………………………..

S_j – горка занята, ( j-1 ) составов в очереди;

………………………………………………………….

Предельная вероятность того, что система находиться в состоянии 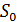, вычисляется по формуле: 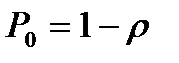, значит, .

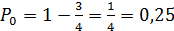Предельные вероятности состояний 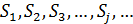вычисляются соответственно по формулам:

; ; ; ; ;….

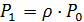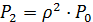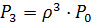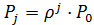Следовательно, , ,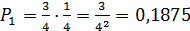

, , , ,

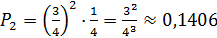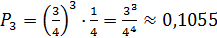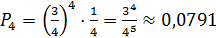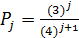б) Среднее число составов, связанных с горкой, вычисляется по формуле:

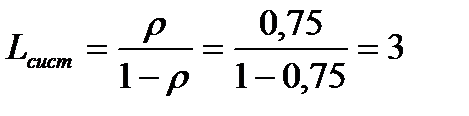состава.

в) Среднее число составов в очереди определяется формулой:

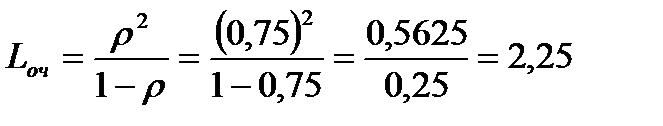состава.

г) Среднее время пребывания состава в СМО:

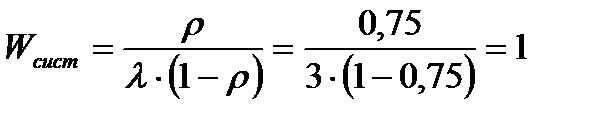час.

д) Среднее время пребывания состава в очереди:

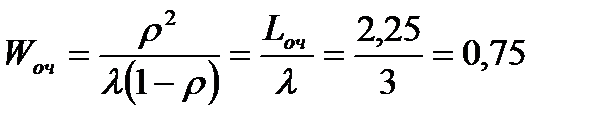час.