Единичная и импульсная функции. Переходная и импульсная характеристики цепи

Единичная и импульсная функции

Широко используется понятие единичной и импульсной функции. Они предназначены для согласования и анализа переходных и импульсных характеристик цепи.

Единичная функция — скачкообразное изменение напряжения от 0 до 1. обозначается :

Импульсная функция (дельта-функция, функция Дирака) — производная по времени от единичной функции.

Переходная и импульсная характеристики цепей

Переходной характеристикой называется закон, по которому изменяется выходное напряжение при единичной функции на входе. Чтобы определить переходную характеристику цепи, надо рассчитать закон изменения выходного напряжения при подаче в цепь постоянного напряжения U, а затем взять это напряжение, равным 1.

Рассмотрим переходную характеристику при включении цепи RC на постоянное напряжение. Известно, что напряжение на конденсаторе при подключении конденсатора цепи RC изменяется по закону

— переходная характеристика цепи RC

Импульсная характеристика цепи представляет собой закон изменения выходного напряжения цепи, если на вход подаётся импульсная функция . Т. к. импульсная функция — это производная по времени от единичной функции, то импульсная характеристика — производная по времени от переходной характеристики:

32. Переходные процессы в цепях 2-го порядка. Переходные процессы в последовательной RLC цепи при её включении на постоянное и синусоидальное напряжение

Включение цепи RLC на постоянное напряжение

При замыкании ключа конденсатор заряжается до напряжения источника по закону переходного процесса.

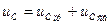
— дифференциальное уравнение II порядка

В зависимости от знака подкоренного выражения получается 3 вида переходного процесса:

1) корни — действительные числа

Апериодический заряд получается, если в контуре большое резистивное сопротивление:

2) критический заряд, если

3) колебательный заряд конденсатора получается, если корни — комплексно сопряжённые числа, . Контур высокодобротный.

При выборе конденсатора необходимо учитывать, что в первый момент времени напряжение на конденсаторе почти в 2 раза превышает ЭДС.

Включение цепи RLC на гармоническое напряжение

При замыкании ключа на конденсаторе устанавливаются гармонические колебания постоянной амплитуды. Контур рассматриваем высокодобротный. .

Переходной процесс может идти 2 путями:

1) если . Если частоты равны, то происходит монотонное увеличение напряжения.

Для цепей второго порядка , время переходного процесса , добротность .

Чем больше добротность, тем медленнее идёт переходной процесс.

2) если , то тогда переходной процесс идёт в виде биений, амплитуда напряжения на конденсаторе изменяется по закону синуса низкой частоты.

33. Понятие о четырёхполюсниках. Классификация четырехполюсников. Эквивалентные схемы четырёхполюсников. Уравнение пассивного четырехполюсника в A-параметрах и h-параметрах

Четырёхполюсник — участок цепи, который имеет 2 входных и 2 выходных зажима.

Классификация четырёхполюсников:

1) активные и пассивные

Активные содержат внутри себя источники или активные элементы. Пассивные — нет.

2) симметричные и несимметричные

Симметричные — если поменять местами входные и выходные зажимы, то режим работы не изменится. Несимметричные — нет.

3) линейные и нелинейные

Линейные — напряжение на выходе линейно зависит от напряжения на входе. Нелинейные — зависимость нелинейная.

4) по конфигурации схемы бывают Т, П, Г-образные четырёхполюсники:

• Т-образный четырёхполюсник

• П-образный

• Прямой Г-образный четырёхполюсник

• Обратный Г-образный четырёхполюсник

Напряжение и ток на входе и выходе четырёхполюсника связаны уравнением. Существует 6 форм записи таких уравнений.

Для исследования транзисторов используют уравнение четырёхполюсников в h-параметрах:

Для исследования пассивных фильтров используют уравнения четырёхполюсников в A-параметрах:

В общем случае параметры — комплексные числа, которые могут иметь размерность, а могут и не иметь. Для A-параметров составлены таблицы — матрицы, по которым можно рассчитать эти параметры, зная сопротивления , , .

Например, для прямого Г-образного четырёхполюсника:

A	B
C	D

Соединяться четырёхполюсники могут:

1) последовательно

2) параллельно

3) последовательно-параллельно

4) каскадно