Пример синтеза регулятора скорости
Пример 2.1. Синтезировать РС, обеспечивающий настройку КС
на ОМ. Для расчета использовать данные двигателя, рассчитанные
в лабораторной работе № 1.
Провести моделирование КС: получить графики переходных функций по задающему воздействию и по моменту сопротивления нагрузки 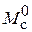 ; построить график ЛЧХ разомкнутого КС; провести анализ результатов моделирования.
; построить график ЛЧХ разомкнутого КС; провести анализ результатов моделирования.
Для моделирования принять следующие параметры:
– постоянная времени БП Тбп = 0,003 с;
– постоянная времени ТГ Ттг = 0,0018 с;
– момент сопротивления нагрузки 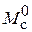 = 180 Н×м;
= 180 Н×м;
– входное напряжение суммирующего усилителя КС 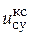 = 10 В;
= 10 В;
– выходное напряжение усилителя регулятора скорости 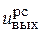 = 2 В.
= 2 В.
Решение.1. Коэффициент передачи тахогенератора:
Ктг = 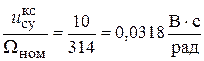 ;
;
коэффициент передачи блока питания:
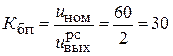 ;
;
постоянные времени РС:
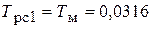 с;
с; 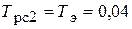 с;
с; 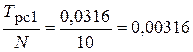 с.
с.
Задаем Трс3 = 0,002 с.
Суммарная малая постоянная времени контура скорости:
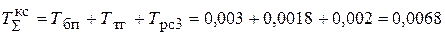 с.
с.
2. Для моделирования построим ССДМ КС. Реализацию динамического звена на входе воздействия момента сопротивления нагрузки (рис. 2.10) необходимо выполнить с добавлением удаленного полюса с малой постоянной времени 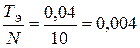 с ССДМ КС
с ССДМ КС
в системе Simulink представлена на рис. 2.10.
Для построения переходной характеристики по управляющему воздействию необходимо нажать пиктограмму Start Simulation. Перед этим устанавливается время интегрирования, в 6 ÷ 10 раз превышающее максимальную постоянную времени контура скорости (в меню Simulation Parameters на вкладке Solver устанавливается время интегрирования Stop Time).
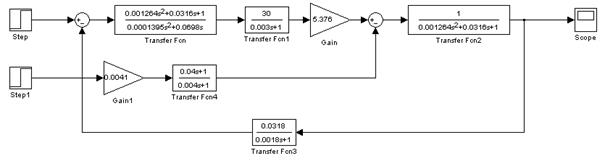
Рис. 2.10. Структурная схема динамической модели контура скорости
в системе Simulink
Для моделирования в блоке Step задаем входное воздействие 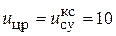 В, а в блоке Step 1 значение момента сопротивления нагрузки
В, а в блоке Step 1 значение момента сопротивления нагрузки 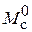
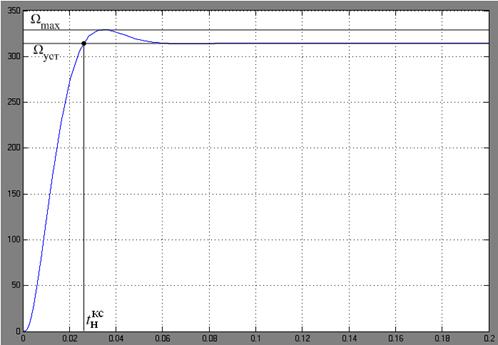
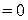 . На рис. 2.11 изображена соответствующая переходная характеристика контура скорости по управляющему воздействию.
. На рис. 2.11 изображена соответствующая переходная характеристика контура скорости по управляющему воздействию.
Ω(t), рад/с
 t, c
t, c
Рис. 2.11. Переходная характеристика контура скорости по управляющему воздействию
Для построения переходной характеристики по моменту сопротивления нагрузки Мс устанавливаем, соответственно, в блоке Step входное воздействие 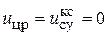 , а в блоке Step 1 – момент сопротивления
, а в блоке Step 1 – момент сопротивления 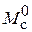
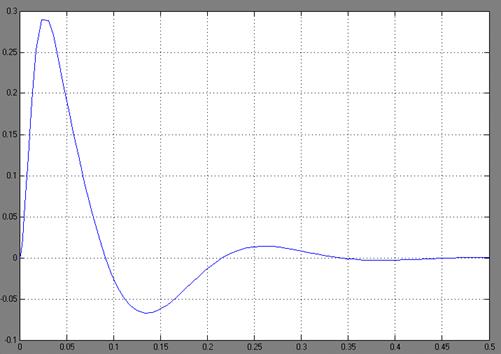
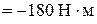 . Полученная переходная характеристика представлена на рис. 2.12.
. Полученная переходная характеристика представлена на рис. 2.12.
W(t), рад/с
 t, c
t, c
Рис. 2.12. Переходная характеристика контура скорости по моменту
сопротивления
3. Переходим к анализу полученных графиков. По графику на
рис. 2.11 определяем максимальное значение угловой скорости вращения двигателя Wmax = 329 рад/с и установившееся значение скорости
Wуст = 314 рад/с. По этим данным рассчитываем перерегулирование:
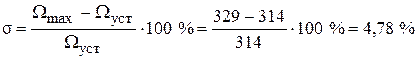 .
.
Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Ттг. Если принять Ттг = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном:
Wтг(s) = Ктг.
При этом суммарную малую постоянную времени КС следует рассчитывать по формуле:
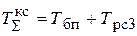 .
.
Время нарастания 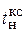 определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Wуст и составляет:
определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Wуст и составляет:
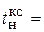 0,026 с.
0,026 с.
Проверяем соответствие полученного значения требованиям настройки на ОМ:
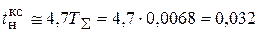 с.
с.
Из анализа графика на рис. 2.12 следует, что при воздействии неизменного по величине момента сопротивления Мс моментная составляющая ошибки ΔWм примерно через 0,4 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жесткой. Увеличение точности обусловлено наличием
в структуре регулятора скорости интегральной составляющей.
4. Для построения ЛЧХ необходимо написать программу в Command Window системы MatLab. Поскольку, ЛЧХ строятся на основе передаточной функции разомкнутого контура скорости, то все передаточные функции соответствующих элементов, входящих в него, необходимо перемножить и получить:
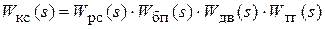 .
.
Обозначая 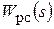 = sys1,
= sys1, 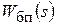 = sys2,
= sys2, 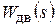 = sys3,
= sys3, 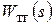 = sys4, составляем программу в соответствии со следующим алгоритмом:
= sys4, составляем программу в соответствии со следующим алгоритмом:
num1 = [Tpc1Tpc2 Tpc1 1];
den1 = [2 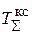 KбпKдвKтгTpc3 2
KбпKдвKтгTpc3 2 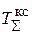 KбпKдвKтг 0];
KбпKдвKтг 0];
sys1 = tf (num1, den1);
num2 = [Kбп];
den2 = [Tбп 1];
sys2 = tf(num2, den2);
num3 = [Kдв];
den3 = [TэTм Tм 1];
sys3 = tf(num3, den3);
num4 = [Kтг];
den4 = [Tтг 1];
sys4 = tf(num4, den4);
sys5 = sys1*sys2*sys3*sys4
В результате решения будет получена искомая передаточная функция разомкнутого КС с численными значениями коэффициентов полиномов числителя и знаменателя b2, b1, b0, d6, d5, d4, d3, d2, d1, d0 = 0:
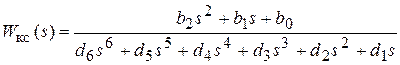 . (2.25)
. (2.25)
Далее переходим к построению ЛЧХ:
w = logspace (– n, m);
num = [b2 b1 b0];
den = [d6 d5 d4 d3 d2 d1 0];
bode(num, den, w)
Значения (– n, m) являются показателями степени при основании 10, указывающем диапазон частот. Обычно ограничиваются диапазоном – 3, 3. В этом случае, частота будет изменяться в пределах 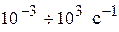 .
.
Для нашего примера, перед тем как применить программу построения ЛЧХ, соответствующую приведенному алгоритму, находим коэффициенты из блоков Transfer Fcn, Transfer Fcn1, Gain, Transfer Fcn2, Transfer Fcn3 схемы, изображенной на рис. 2.10:
num1=[0.001264 0.0316 1];
>> den1=[0.0001395 0.0698 0];
>> sys1=tf(num1, den1)
Transfer function:
0.001264 s^2 + 0.0316 s + 1
---------------------------
0.0001395 s^2 + 0.0698 s
>> num2=[30];
den2=[0.003 1];
sys2=tf(num2, den2)
Transfer function:
-----------
0.003 s + 1
>> num3=[5.376];
den3=[0.001264 0.0316 1];
sys3=tf(num3, den3)
Transfer function:
5.376
---------------------------
0.001264 s^2 + 0.0316 s + 1
>> num4=[0.0318];
den4=[0.0018 1];
sys4=tf(num4, den4)
Transfer function:
0.0318
------------
0.0018 s + 1
>> sys5=sys1*sys2*sys3*sys4
Transfer function:
0.006483 s^2 + 0.1621 s + 5.129
-----------------------------------------------------------------------------------------
9.522e-013 s^6 + 1.347e-009 s^5 + 6.336e-007 s^4 + 0.0001043 s^3 + 0.00268 s^2 + 0.0698 s
>> w=logspace (-3, 3);
>> num=[0.006483 0.1621 5.129];
>> den=[9.522e-013 1.347e-009 6.336e-007 0.0001043 0.00268 0.0698 0];
>> bode(num, den, w)
Результаты моделирования представлены на рис. 2.13.
Из анализа графиков видно, что запасы устойчивости по фазе и амплитуде составляют: Lз = 14,8 дБ (Gain Margin) и 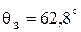 (Phase Margin), соответственно.
(Phase Margin), соответственно.
Напомним, что запас устойчивости по амплитуде Lз определяется как разность между линией 0 дБ и значением логарифмической амплитудно-частотной характеристики (ЛАЧХ) на частоте, соответствующей точке пересечения графика фазовой частотной характеристики со значением 180°.
Запас устойчивости по фазе 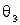 вычисляется по формуле:
вычисляется по формуле:
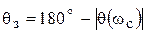 .
.
Значение фазы 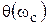 соответствует частоте среза wс, т.е. точке пересечения графика ЛАЧХ с линией 0 дБ.
соответствует частоте среза wс, т.е. точке пересечения графика ЛАЧХ с линией 0 дБ.
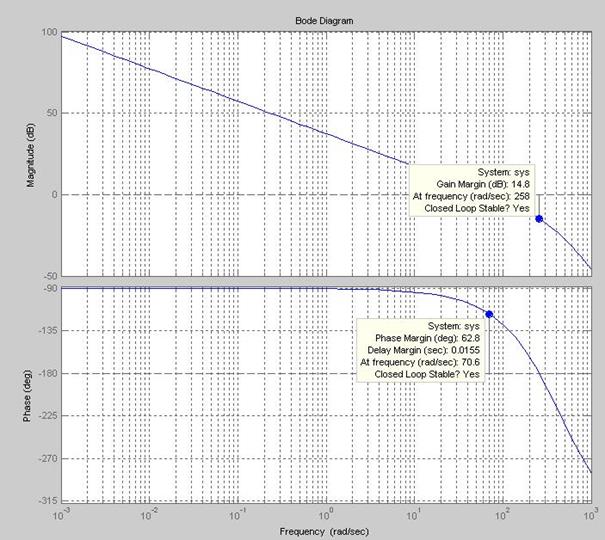
Рис. 2.13. Логарифмические частотные характеристики контура скорости
Результаты моделирования подтверждают правильность расчета параметров РС и позволяют сделать вывод о том, что КС настроен на ОМ.
Отчетные материалы
1. Расчет параметров структурной схемы динамической модели контура скорости.
2. Структурная схема динамической модели.
3. Графики переходных характеристик по управляющему воздействию и моменту сопротивления и их анализ.
4. ЛЧХ и их анализ.
Контрольные вопросы
1. Дать определение настройки на ОМ.
2. Дать определение настройки на СО.
3. Записать передаточную функцию замкнутого контура, настроенного на ОМ.
4. Записать передаточную функцию разомкнутого контура, настроенного на СО.
5. Перечислить показатели качества процесса управления
с применением стандартных настроек.
6. Пояснить порядок моделирования контура скорости
с применением системы MatLab.
ЛАБОРАТОРНАЯ РАБОТА № 3
