Индукция магнитного поля в центре и на оси кругового витка с током

Вначале решим более общую задачу нахождения магнитной индукции на оси витка с током. Для этого сделаем рисунок 3.8, на котором изобразим элемент тока 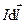и вектор магнитной индукции 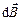, который он создает на оси кругового контура в некоторой точке .

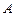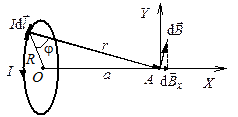
Рис. 3.8 Определение магнитной индукции

на оси кругового витка с током

Вектор магнитной индукции 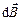, создаваемый бесконечно малым элементом контура 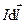может быть определен с помощью закона Био-Савара-Лапласа (3.10).

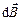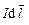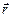Как следует из правил векторного произведения, магнитная индукция будет перпендикулярна плоскости, в которой лежат вектора и , поэтому модуль вектора 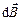будет равен

.

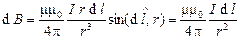Для нахождения полной магнитной индукции от всего контура необходимо векторно сложить 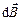от всех элементов контура, т. е. фактически сосчитать интеграл по длине кольца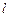

.

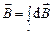Данный интеграл можно упростить, если представить 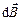в виде суммы двух составляющих 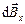и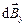

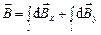
При этом в силу симметрии 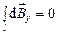, поэтому результирующий вектор магнитной индукции будет лежать на оси 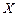. Следовательно, для нахождения модуля вектора нужно сложить проекции всех векторов 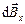, каждая из которых равна

.

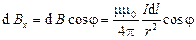Учитывая, что 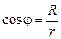и 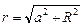, получим для интеграла следующее выражение

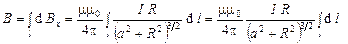. (3.18)

Нетрудно заметить, что вычисление получившегося интеграла даст длину контура, т. е. 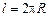. В итоге суммарная магнитная индукция, создаваемая круговым контуром на оси в точке 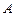, равна

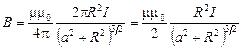. (3.19)

Используя магнитный момент контура, формулу (3.19) можно переписать следующим образом

.

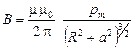Теперь отметим, что полученное в общем виде решение (3.19) позволяет проанализировать предельный случай, когда точка 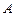помещена в центре витка. В этом случае 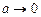и решение для магнитной индукции поля в центре кольца с током примет вид

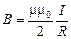. (3.20)

Результирующий вектор магнитной индукции (3.19) направлен вдоль оси тока, а его направление связано с направлением тока правилом правого винта (рис. 3.9).

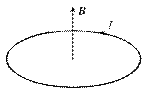
Рис. 3.9 Определение магнитной индукции

в центре кругового витка с током

Индукция магнитного поля в центре дуги окружности

Данная задача может быть решена как частный случай рассмотренной в предыдущем пункте задачи. В этом случае интеграл в формуле (3.18) следует брать не по всей длине окружности, а только по ее дуге l. А также учесть то, что индукция ищется в центре дуги, поэтому 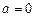. В результате получим

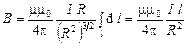, (3.21)

где 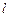– длина дуги; 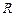– радиус дуги.

5 Вектор индукции магнитного поля движущегося в вакууме точечного заряда (без вывода формулы)

,

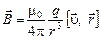где 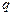– электрический заряд; 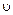– постоянная нерелятивистская скорость; 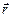– радиус-вектор, проведенный от заряда к точке наблюдения.

Силы Ампера и Лоренца

Опыты по отклонению рамки с током в магнитном поле показывают, что на всякий проводник с током, помещенный в магнитное поле, действует механическая сила, называемая силой Ампера.

Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:

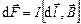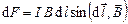; , (3.22)

где 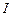– сила тока; 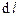– элемент длины провода (вектор 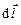совпадает по направлению с током 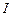); 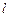– длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.

Если прямолинейный проводник длиной 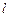находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.10):

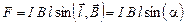. (3.23)

Сила Ампера всегда направлена перпендикулярно плоскости, содержащей векторы 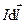и , а ее направление как результат векторного произведения определяется правилом правого винта: если смотреть вдоль вектора 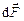, то поворот от 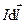к по кратчайшему пути должен происходить по часовой стрелке.

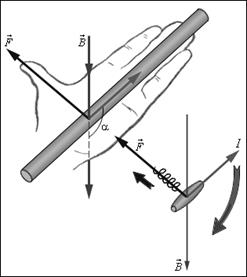
Рис. 3.10 Правило левой руки и правило буравчика для силы Ампера

С другой стороны, для определения направления силы Ампера можно также применить мнемоническоеправило левой руки (рис. 3.10): нужно поместить ладонь так, чтобы силовые линии магнитной индукции входили в нее, вытянутые пальцы показывали направление тока, тогда отогнутый большой палец укажет направление силы Ампера.

Исходя из формулы (3.22), найдем выражение для силы взаимодействия двух бесконечно длинных, прямых, параллельных друг другу проводников, по которым текут токи I₁ и I₂ (рис. 3.11) (опыт Ампера). Расстояние между проводами равно a.

Определим силу Ампера dF₂₁, действующую со стороны магнитного поля первого тока I₁ на элемент l₂dl второго тока.

Величина магнитной индукции этого поля B₁ в точке расположения элемента второго проводника с током равна

.

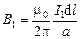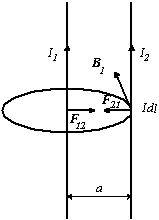
Рис. 3.11 Опыт Ампера по определению силы взаимодействия

двух прямолинейных токов

Тогда с учетом (3.22) получим

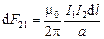. (3.24)

Рассуждая точно так же, можно показать, что сила Ампера, действующая со стороны магнитного поля, создаваемого вторым проводником с током, на элемент первого проводника I₁dl , равна

,

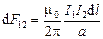т. e. dF₁₂ = dF₂₁. Таким образом, мы вывели формулу (3.1), которая была получена Ампером экспериментальным путем.

На рис. 3.11 показано направление сил Ампера. В случае, когда токи направлены в одну и ту же сторону, то это ‑ силы притяжения, а в случае токов разного направления ‑ силы отталкивания.

Из формулы (3.24), можно получить силу Ампера, действующую на единицу длины проводника

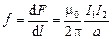. (3.25)

Таким образом, сила взаимодействия двух параллельных прямых проводников с токами прямо пропорциональна произведению величин токов и обратно пропорциональна расстоянию между ними.

Закон Ампера утверждает, что на элемент с током, помещенный в магнитное поле, действует сила. Но всякий ток есть перемещение заряженных частиц. Естественно предположить, что силы, действующие на проводник с током в магнитном поле, обусловлены силами, действующими на отдельные движущиеся заряды. Этот вывод подтверждается рядом опытов (например, электронный пучок в магнитном поле отклоняется).

Найдем выражение для силы, действующей на заряд, движущийся в магнитном поле, исходя из закона Ампера. Для этого в формулу, определяющую элементарную силу Ампера

,

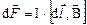подставим выражение для силы электрического тока

,

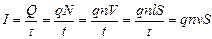где I – сила тока, протекающего через проводник; Q – величина полного заряда протекшего за время t; q – величина заряда одной частицы; N – общее число заряженных частиц, прошедших через проводник объемом V, длиной l и сечением S; n – число частиц в единице объема (концентрация); v – скорость частицы.

В результате получим:

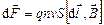. (3.26)

Направление вектора 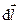совпадаёт с направлением скорости v, поэтому их можно поменять местами.

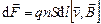. (3.27)

Эта сила действует на все движущиеся заряды в проводнике длиной 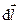и сечением S, число таких зарядов:

.

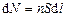Следовательно, сила, действующая на один заряд, будет равна:

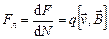. (3.28)

Формула (3.28) определяет силу Лоренца, величина которой

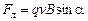, (3.29)

где a - угол между векторами скорости частицы и магнитной индукции.

В экспериментальной физике часто встречается ситуация, когда заряженная частица движется одновременно и в магнитном и электрическом поле. В этом случае рассматривают полную силу Лоренца в виде

,

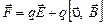где 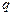– электрический заряд; 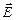– напряженность электрического поля; 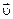– скорость частицы; – индукция магнитного поля.

Только в магнитном поле на движущуюся заряженную частицу действует магнитная составляющая силы Лоренца (рис. 3.12)

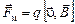. (3.30)

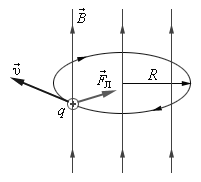
Рис. 3.12 Сила Лоренца

Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.

Взаимная ориентация трех векторов ‑ 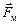, 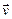и , входящих в (3.30), показана на рис. 313 для положительно заряженной частицы.

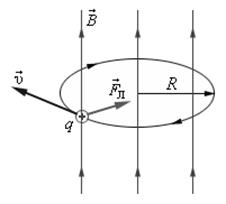
Рис. 3.13 Сила Лоренца, действующая на положительный заряд

Как видно из рис. 3.13, если частица влетает в магнитное поле под углом 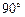к силовым линиям , то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:

; ,

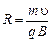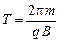где 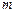– масса частицы.

Отношение магнитного момента 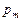к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,

,

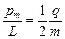где 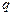‑ заряд частицы; т ‑ масса частицы.

Рассмотрим общий случай движения заряженной частицы в однородном магнитном поле, когда ее скорость направлена под произвольным углом a к вектору магнитной индукции (рис. 3.14). Если заряженная частица влетает в однородное магнитное поле под углом 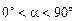, то она движется по винтовой линии.

Разложим вектор скорости на составляющие v_|| (параллельную вектору ) и v_^(перпендикулярную вектору ):

.

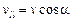
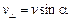Наличие v_^ приводит к тому, что на частицу будет действовать сила Лоренца и она будет двигаться по окружности радиусом R в плоскости перпендикулярной вектору :

.

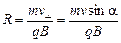Период такого движения (время одного витка частицы по окружности) равен

.

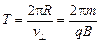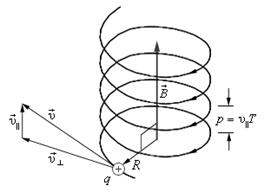
Рис. 3.14 Движение по винтовой линии заряженной частицы

в магнитном поле

За счет наличия v_|| частица будет двигаться равномерно вдоль , так как на v_|| магнитное поле не действует.

Таким образом, частица участвует одновременно в двух движениях. Результирующая траектория движения представляет собой винтовую линию, ось которой совпадает с направлением индукции магнитного поля. Расстояние h между соседними витками называется шагом винтовой линии и равно:

.

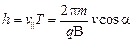Действие магнитного поля на движущийся заряд находит большое практическое применение, в частности, в работе электронно-лучевой трубки, где используется явление отклонения заряженных частиц электрическим и магнитным полями, а также в работе масс-спектрографов, позволяющих определить удельный заряд частиц (q/m) и ускорителей заряженных частиц (циклотронов).

Рассмотрим один такой пример, назыаемый «магнитной бутылкой» (рис. 3.15). Пусть неоднородное магнитное поле создано двумя витками с токами, протекающими в одном направлении. Сгущение линий индукции в какой-либо пространнственной области означает большее значение величины магнитной индукции в этой области. Индукция магнитного поля вблизи витков с током больше, чем в пространстве между ними. По этой причине радиус винтовой линии траектории частицы, обратно пропорциональный модулю индукции, меньше вблизи витков, чем в пространстве между ними. После того, как частица, двигаясь вправо по винтовой линии, пройдет среднюю точку, сила Лоренца, действующая на чатицу, приобретает компоненту 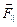, тормозящую ее движение вправо. В определенный момент эта компонента силы останавливает движение частицы в этом направлении и отталкивает ее влево к витку 1. При приближении заряженной частицы к витку 1 она также тормозится и начинает циркулировать между витками, оказавшись в магнитной ловушке, или между «магнитными зеркалами». Магнитные ловушки используются для удержания в определенной области пространства высокотемпературной плазмы ( 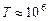К) при управляемом термоядерном синтезе.

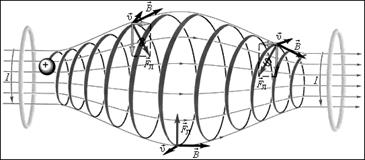
Рис. 3.15 Магнитная «бутылка»

Закономерностями движения заряженных частиц в магнитном поле можно объяснить особенности движения космических лучей вблизи Земли. Космические лучи – это потоки заряженных частиц большой энергии. При приближении к поверхности Земли эти частицы начинают испытывать действие магнитного поля Земли. Те из них, которые направляются к магнитным полюсам, будут двигаться почти вдоль линий земного магнитного поля и навиваться на них. Заряженные частицы, подлетающие к Земле вблизи экватора, направлены почти перпендикулярно к линиям магнитного поля, их траектория будет искривляться. и лишь самые быстрые из них достигнут поверхности Земли (рис. 3.16).

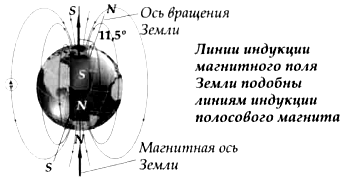
Рис. 3.16 Образование Полярного сияния

Поэтому интенсивность космических лучей доходящих до Земли вблизи экватора, заметно меньше, чем вблизи полюсов. С этим связан тот факт что, Полярное сияние наблюдается главным образом в приполярных областях Земли.

Эффект Холла

В 1880г. американский физик Холл провел следующий опыт: он пропускал постоянный электрический ток I через пластинку из золота и измерял разность потенциалов 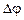между противолежащими точками A и C на верхней и нижней гранях (рис. 3.17).

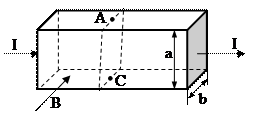
Рис. 3.17 Эффект Холла

В отсутствии магнитного поля 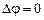, т. к. для однородной пластины поперечное сечение является эквипотенциальной поверхностью. Когда пластины помещаются в однородное магнитное поле с индукцией , перпендикулярное к ее боковым граням ‑ между точками A и C возникала разность потенциалов. Это явление было позднее названо эффектом Холла.

Экспериментально было обнаружено, что

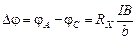, (3.31)

где I ‑ сила тока; B ‑ индукция магнитного поля; b ‑ ширина пластины; 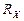‑ постоянная Холла.

Дальнейшее исследование показало, что эффект Холла наблюдается во всех проводниках и полупроводниках. Величина константы Холла зависит от материала пластины, причем этот коэффициент для одних веществ положителен, а для других ‑ отрицателен.

Явление Холла можно объяснить, исходя из силы Лоренца. На заряд, движущийся в магнитном поле с индукцией B, действует сила Лоренца

.

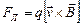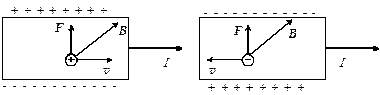
Рис. 3.18 Знак эффекта Холла

Если носителями тока в веществе являются положительные заряды то под действием силы Лоренца эти заряды q отклоняются к верхней грани (при выбранных направлениях и 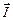). Следовательно, вблизи верхней грани возникнет избыток зарядов, а вблизи нижней грани – недостаток зарядов, т. е. возникает разность потенциалов. В случае отрицательных зарядов, как видно из рисунка 3.18, знак разности потенциалов будет противоположым.

Найдем теперь выражение для 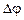. При возникновении разности потенциалов в пластине возникает электрическое поле в вертикальном направлении. Со стороны этого электрического поля на заряд q будет действовать сила 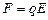, направленная против силы Лоренца. При некотором значении 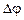эти силы уравновесят друг друга, и установится равновесный процесс прохождения тока

,

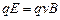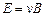.(3.32)

Если пластина достаточно длинная и широкая, то поперечное электрическое поле можно считать однородным. Для однородного поля можно написать связь между E и 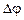в виде:

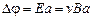. (3.33)

Силу тока I можно выразить следующим образом:

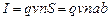, (3.34)

где v ‑ скорость упорядоченного движения зарядов; n ‑ число зарядов в единице объема; 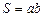– площадь поперечного сечения пластины.

Отсюда

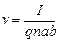, (3.35)

подставляя (3.35) в (3.33) получим

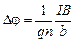. (3.36)

Сравнивая эту формулу с экспериментальной (3.31), имеем

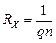. (3.37)

Отсюда видно, что, знак константы Холла совпадает со знаком заряда q носителей тока. В полупроводниках носителями тока могут быть электроны ( 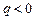) и положительные дырки ( 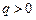). На основании измерения константы Холла для полупроводников можно судить о природе его проводимости. При электронной проводимости 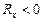, при дырочной проводимости .

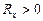С помощью константы Холла можно также определить концентрацию носителей тока, если характер проводимости и заряд носителей тока известны (например, для металлов):

.

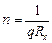На принципе, похожем на эффект Холла, основана работа МГД- генераторов (магнитогидродинамических генераторов). В эффекте Холла используется ток проводимости, а можно использовать конвекционный ток. Например, по трубе продувается поток раскаленных газов (следовательно, ионизированных) в магнитном поле. В трубу вводятся электроды, на них возникает разность потенциалов. Величина 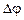оказывается пропорциональной скорости движения газа. Для увеличения электропроводимости должна быть велика концентрация ионов n, что можно достигнуть повышением температуры газа. Кроме того, в поток газа вводятся специальные присадки ‑ элементы с малой энергией ионизации.

К.П.Д. МГД-генераторов может достигать 50…60%, в то время, как у тепловых электростанций 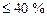. Также преимуществом МГД-генераторов является то, что в них нет никаких механических движущихся частей и, следовательно, потерь на преодоление трения.