Виды параллельных колебательных контуров. Контуры с неполным включением

Автотрансформаторное (неполное) включение контура

Схема контура I-го вида

Эта цепь удовлетворительно работает, если соблюдается условие .

На практике — внутреннее сопротивление лампы или транзистора, т. е. вполне определённая величина. — тоже определённая величина, поэтому это равенство может не соблюдаться.

Чтобы это равенство соблюдалось, уменьшают . Для этого используют неполное (автотрансформаторное) включение контура. Часть индуктивности катушки или ёмкости конденсатора переносят из одной ветви в другую так, чтобы общая ёмкость или индуктивность контура, а значит и резонансная частота, не изменились.

Схема контура II-го вида

Вводят понятие коэффициент включения контура:

Доказано, что контура II вида равно:

Т. к. , то

Схема контура III вида

Т. к. , то

Неполное включение контура служит для уменьшения входного сопротивления контура на резонансной частоте.

Дополнение. Сравнение последовательного и параллельного контуров

Последовательный контур	Параллельный контур
1. Резонанс напряжений	1. Резонанс токов
2.	2.
3.	3.
4. В последовательном контуре добротность показывает, во сколько раз напряжение на реактивных элементах (на выходе) больше, чем напряжение на входе. Поэтому это явление называется резонанс напряжений.	4. В параллельном контуре добротность показывает, во сколько раз ток ветвей больше общего тока в момент резонанса. Поэтому это явление называется резонанс токов.

Электронные аналоги колебательных контуров. Электронный колебательный контур, его избирательные свойства. Достоинства электронного колебательного контура по сравнению с пассивными колебательными контурами. Гиратор

Электронный колебательный контур

Начертим схему последовательного контура, чтобы на выходе стоял резистор:

Известно, что последовательный контур обладает избирательностью по напряжению. Докажем, при каких условиях это будет. Рассмотрим, какой вид имеет комплексная передаточная характеристика контура:

Вывод: если знаменатель комплексного коэффициента передачи цепи имеет вид квадратного уравнения , то эта цепь обладает избирательностью по напряжению. Выражают некоторые величины через B и D:

Можно получить избирательные свойства цепи, используя активные элементы ОУ с отрицательными обратными связями:

Для этой цепи рассчитан комплексный коэффициент передачи, считая :

Из формулы видно, что знаменатель передаточной функции имеет вид квадратного уравнения, значит электронный контур обладает избирательностью по напряжению, и его передаточная характеристика имеет резонансный вид:

Рассчитаем некоторые величины через коэффициенты B и D:

Электронный контур имеет следующие преимущества перед обычными контурами:

1. можно регулировать , , 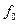Q и П резисторами;

2. большое входное сопротивление кОм, малое выходное сопротивление;

3. схема компактная, т. к. нет катушек индуктивности.

Электронная индуктивность (гиратор)

Обычные катушки индуктивности обладают рядом недостатков:

1) сказываются помехи, создаваемые магнитными полями других катушек или цепей;

2) большие габариты;

3) магнитная проницаемость, а значит и индуктивность катушки, зависят от частоты, поэтому используют схему, состоящую из активных элементов (ОУ), резисторов и конденсаторов.

Электронные цепи, обладающие индуктивными свойствами, называются гираторами. Если считать все сопротивления R приблизительно одинаковыми, то входное сопротивление такой цепи: .

Известно, что входное сопротивление индуктивности , значит входное сопротивление такой цепи изменяется по закону индуктивности, где в качестве L_Э существует:

, тогда .

Электронная индуктивность имеет малые габариты, может быть выполнена в микроэлектронном исполнении и не подвержена влиянию внешних электромагнитных полей.

18. Реактивные двухполюсники. Определение. Одно-, двух-, трехэлементные реактивные двухполюсники. Построение характеристик, χ = F(ω), φ = F(ω). Нулевые и полюсные частоты

Реактивные двухполюсники

Реактивными двухполюсниками называются цепи, имеющие 2 входных зажима и состоящие из индуктивностей и емкостей.

Главной зависимостью двухполюсника является зависимость его реактивного сопротивления от частоты, т. е. , где x — реактивное сопротивление.

Одноэлементные реактивные двухполюсники

Двухэлементные реактивные двухполюсники

1. Последовательное соединение L и C

На некоторой частоте . Наступает резонанс напряжений. Такие частоты называются нулями функции и обозначаются кружком .

Признак последовательного двухполюсника: