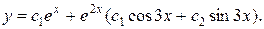Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Решение линейного неоднородного дифференциального уравнения второго порядка

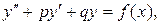(1)

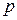где и 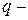постоянные величины, 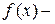функция специального вида.

Пусть правая часть уравнения (1) имеет специальный вид. Тогда частное решение 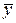этого уравнения можно подобрать в зависимости от вида 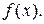Такой метод называют методом неопределенных коэффициентов.

1) Пусть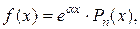

где 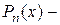многочлен степени .

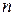Тогда частное решение 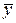подбирают в виде:

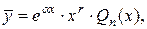
где а) 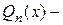многочлен степени 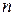с неопределенными коэффициентами, которые надо будет определить методом неопределенных коэффициентов;

б) 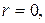если число 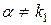и 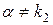(корням характеристического уравнения);

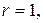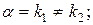
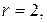если

если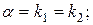

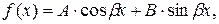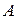2) Пусть где и 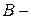заданные числа, причем хотя бы одно из чисел 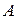и 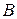не равно нулю. Тогда частное решение 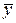подбирают в виде:

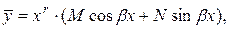
где а) 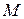и 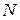– неопределенные числа, которые надо будет определить методом неопределенных коэффициентов;

б) 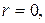если число 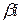не является корнем характеристического уравнения;

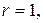если число 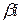является корнем характеристического уравнения.

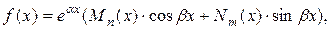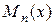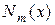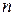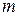3) Пусть где и многочлены степени и соответственно, причем один из этих многочленов может быть равен нулю. Тогда частное решение 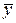подбирают в виде:

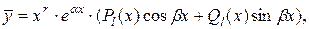
где а) 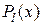и 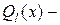многочлены степени 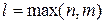с неопределенными коэффициентами, которые надо будет определить методом неопределенных коэффициентов;

б) 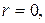если число 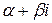не является корнем характеристического уравнения;

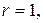если число 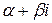является корнем характеристического уравнения.

Решение линейного неоднородного дифференциального уравнения второго порядка методом вариации произвольных постоянных

Пусть дано ЛНДУ второго порядка с постоянными коэффициентами

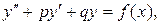(1)

и соответствующее уравнению (1) ЛОДУ:

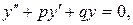(2)

для которого известна фундаментальная система решени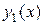й и 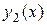. Тогда общее решение ЛОДУ (2) запишется в виде:

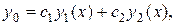(3)

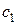где и 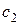– произвольные постоянные.

По методу вариации произвольных постоянных общее решение ЛНДУ (1) ищется в виде (3), считая, что 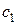и 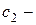не постоянные, а некоторые функции от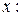

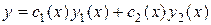. (4)

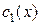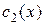Для нахождения и составим систему двух уравнений:

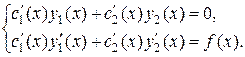
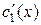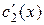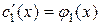Решая эту систему, найдем и :

и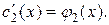

Интегрируя полученные равенства, получим:

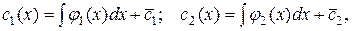
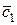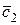где и – произвольные постоянные.

Подставляя найденные 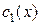и 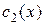в формулу (4), получим общее решение ЛНДУ (1):

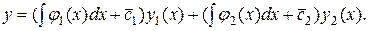
Примеры с решениями

Пример 1. Решить уравнение:

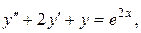
Решение:

1) Решим соответствующее ЛОДУ:

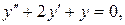
Его характеристическое уравнение:

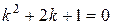
Решим это уравнение.

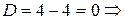корни действительные и равные: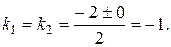

Следовательно, общее решение ЛОДУ имеет вид:

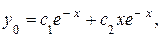
где 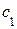и 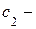произвольные постоянные.

2) Правая часть ЛНДУ: 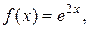т.е. имеет вид: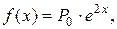

где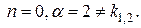

Поэтому 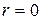и частное решение данного уравнения ищем в виде:

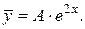
Отсюда находим 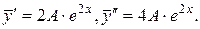Подставляя 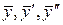вместо 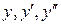в данное уравнение, получим равенство:

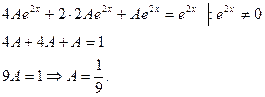
Следовательно, частное решение данного уравнения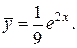

3) Найдем общее решение данного уравнения, воспользовавшись теоремой 2 (из §2):

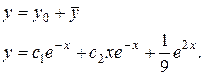
Ответ: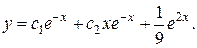

Пример 2. Решить уравнение:

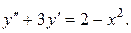
Решение:

1) Решим соответствующее ЛОДУ:

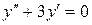
Его характеристическое уравнение:

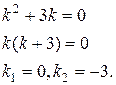
Следовательно, общее решение ЛОДУ имеет вид:

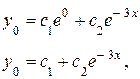
где 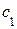и 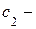произвольные постоянные.

2) Правая часть ЛНДУ: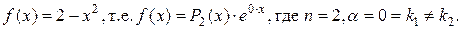

Поэтому 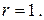Значит, частное решение ЛНДУ ищем в виде:

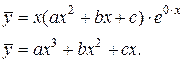
Отсюда находим 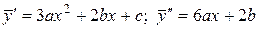. Подставляя 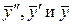вместо 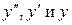в данное уравнение, получим равенство:

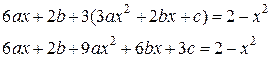
Приравниваем коэффициенты при одинаковых степенях:

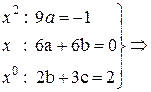
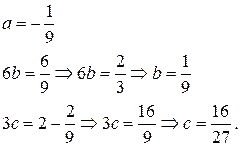
Следовательно, частное решение данного ЛНДУ имеет вид:

3) Найдем общее решение данного уравнения:

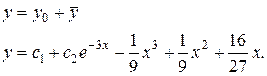
Ответ: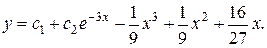

Пример 3. Решить уравнение:

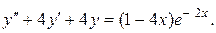
Решение:

1) Решим соответствующее ЛОДУ:

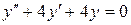
Его характеристическое уравнение:

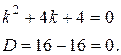
Поэтому корни характеристического уравнения действительные и равные:

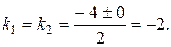
Следовательно, общее решение ЛОДУ имеет вид:

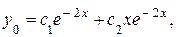
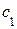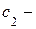где и произвольные постоянные.

2) Правая часть данного ЛНДУ: 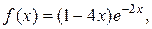т.е.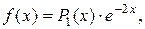

где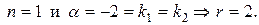

Поэтому частное решение ЛНДУ ищем в виде:

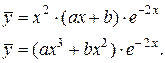
Отсюда находим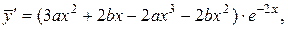

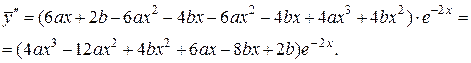
Подставляя 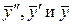вместо 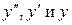в данное уравнение, получим равенство:

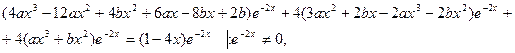
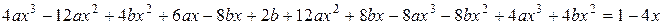
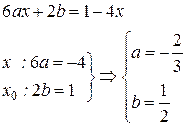
Следовательно, частное решение данного ЛНДУ имеет вид:

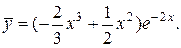
3) Найдем общее решение данного уравнения:

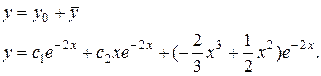
Ответ: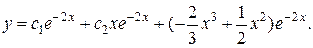

Пример 4. Решить уравнение:

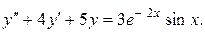
Решение:

1) Решим соответствующее ЛОДУ:

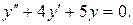
Его характеристическое уравнение:

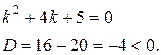
Поэтому корни характеристического уравнения комплексно-сопряженные:

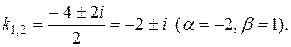
Следовательно, общее решение ЛОДУ имеет вид:

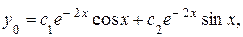
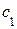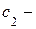где и произвольные постоянные.

2) Правая часть данного ЛНДУ: 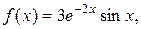т.е.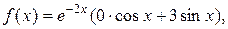

где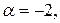

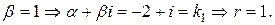
Поэтому частное решение ЛНДУ ищем в виде:

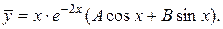
Отсюда находим 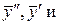подставляем 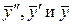вместо 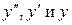в данное уравнение.

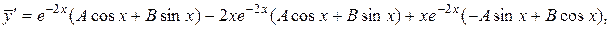
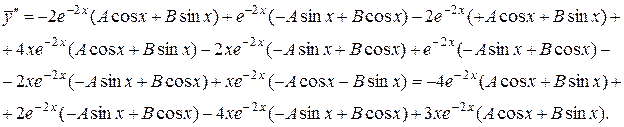
Подстановка в данное уравнение:

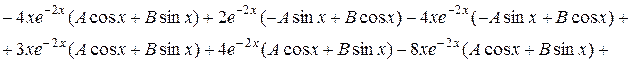
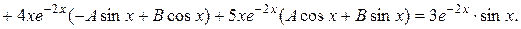
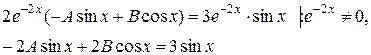
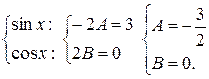
Следовательно, частное решение ЛНДУ:

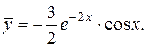
3) Найдем общее решение данного ЛНДУ:

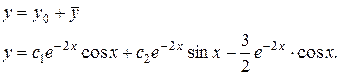
Ответ: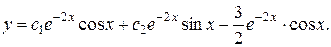

Пример 5. Решить уравнение:

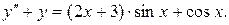
Решение:

1) Решим соответствующее ЛОДУ:

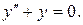
Его характеристическое уравнение:

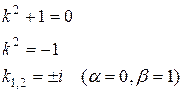
Следовательно, общее решение ЛОДУ имеет вид:

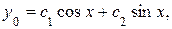
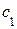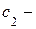где и произвольные постоянные.

2) Правая часть данного ЛНДУ:

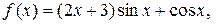т.е.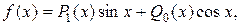

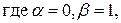
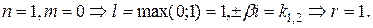
Значит, частное решение данного уравнения ищем в виде:

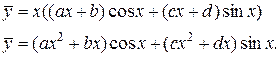
Отсюда находим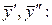

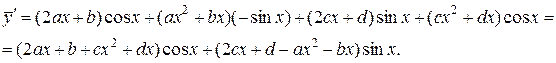
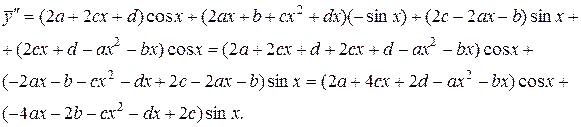
Подстановка в данное ЛНДУ:

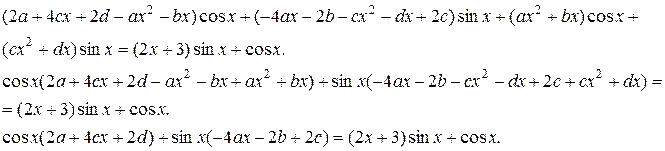
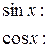
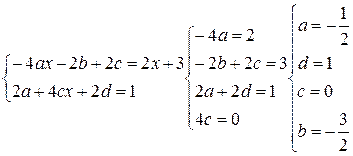
Следовательно, частное решение ЛНДУ:

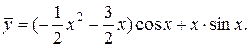
3) Найдем общее решение ЛНДУ:

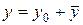
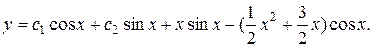
Ответ: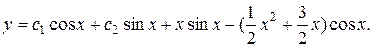

Пример 6. Решить задачу Коши:

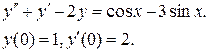
Решение:

1) Найдем общее решение соответствующего ЛОДУ:

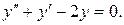
Его характеристическое уравнение:

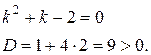
Корни этого уравнения действительные и различные:

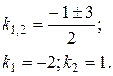
Следовательно, общим решением ЛОДУ является функция:

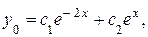
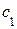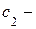где и произвольные постоянные.

2) Правая часть данного ЛНДУ:

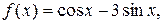т.е. 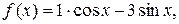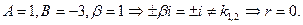Тогда частное решение 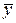данного ЛНДУ надо подбирать в виде:

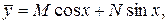
где 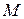и 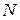– некоторые числа, которые определяются методом неопределенных коэффициентов.

Найдём 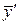и 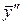и подставим 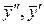и 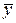вместо 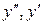и 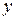в заданное ЛНДУ:

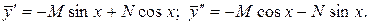
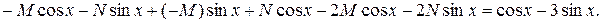
Приравняем коэффициенты при 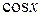и :

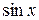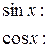
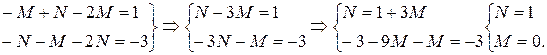
Следовательно, частным решением данного ЛНДУ является

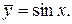
3) Найдем общее решение заданного ЛНДУ:

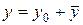
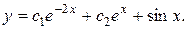
4) Решим задачу Коши: найдем частное решение ЛНДУ, удовлетворяющее заданным начальным условиям:

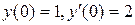
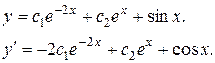
Подставим в эти функции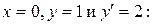

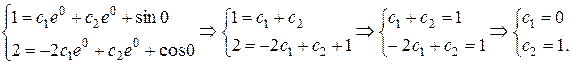
Следовательно, частное решение ЛНДУ, удовлетворяющее заданным начальным условиям, задается функцией:

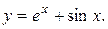
Ответ: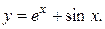

Пример 7. Решить уравнение:

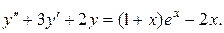
Решение:

1) Решим соответствующее ЛОДУ:

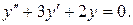
Его характеристическое уравнение:

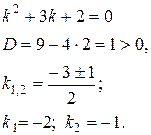
Следовательно, общее решение ЛОДУ имеет вид:

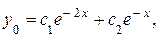
где 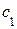и 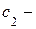произвольные постоянные.

2) Правая часть данного ЛНДУ состоит из двух различных по виду слагаемых:

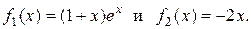
Поэтому частное решение будет складываться из двух функций

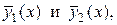каждая из которых будет частным решением для уравнений:

(*)

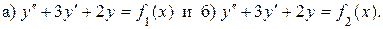
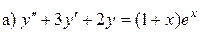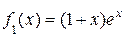, т.е.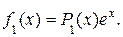

где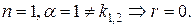

Поэтому 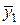ищем в виде:

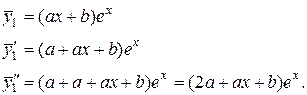
Подставим найденные производные в уравнение (*):

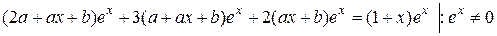
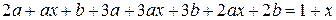
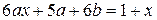
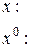
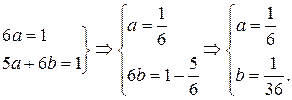
Следовательно, частное решение для уравнения (*):

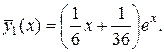
б) (**)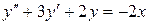

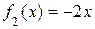, т.е.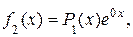

где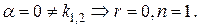

Поэтому частное решение 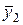ищем в виде:

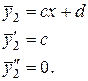
Подставим найденные производные в уравнение (**):

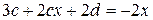
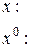
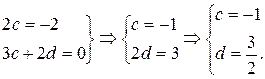
Следовательно, частное решение для уравнения (**):

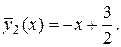
Значит, частным решением для данного ЛНДУ будет сумма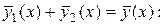

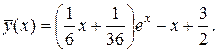
3) Найдем общее решение ЛНДУ:

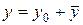
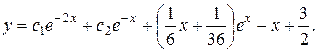
Ответ: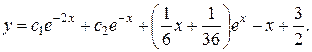

Пример 8. Решить уравнение:

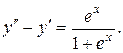
Решение:

1) Решим соответствующее ЛОДУ:

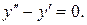
Его характеристическое уравнение:

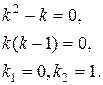
Следовательно, общим решением ЛОДУ будет функция:

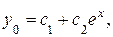
где 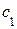и 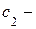произвольные постоянные.

2) Правая часть данного ЛНДУ: 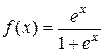не соответствует методу подбора частного решения этого уравнения. Поэтому применим метод вариации произвольных постоянных. Будем искать общее решение данного ЛНДУ в том же виде, в котором получили общее решение его ЛОДУ, но вместо 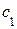и 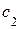берем функции:

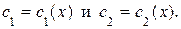
Значит, общее решение ЛНДУ ищем в виде:

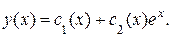
Для нахождения функций 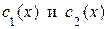составим систему двух уравнений:

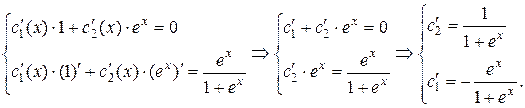
Проинтегрируем найденные :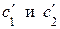

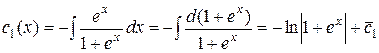
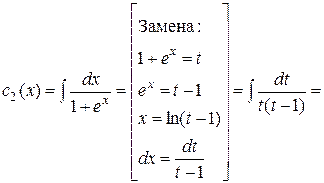
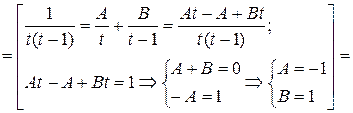
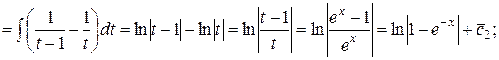
Итак,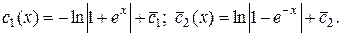

Следовательно, общее решение данного уравнения:

.

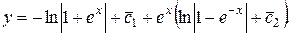Ответ: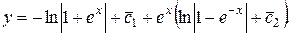

Пример 9. Решить задачу Коши:

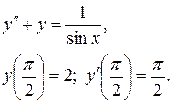
Решение:

1) Решим соответствующее ЛОДУ:

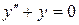
Его характеристическое уравнение:

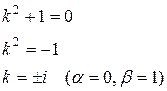
Следовательно, общим решением ЛОДУ будет функция:

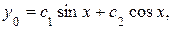
где 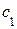и 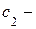произвольные постоянные.

2) Правая часть данного ЛНДУ:

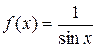не соответствует методу подбора частного решения этого уравнения. Поэтому применяем метод вариации произвольных постоянных:

Общее решение ЛНДУ ищем в виде:

(***)

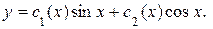Для нахождения 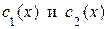составим систему двух уравнений:

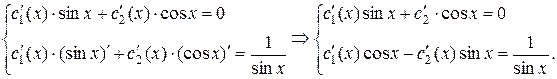
Решим систему по правилу Крамера:

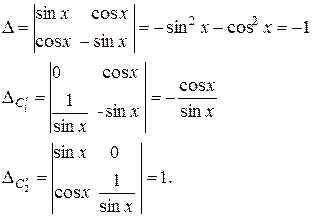
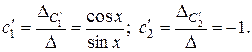
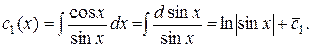
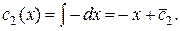
Итак,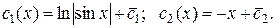

Следовательно, общее решение данного ЛНДУ можно записать, подставляя

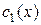и 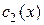в функцию (***):

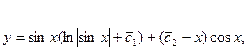
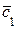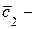где и произвольные постоянные.

3) Решим задачу Коши, т.е. найдем частное решение ЛНДУ, удовлетворяющее заданным начальным условиям:

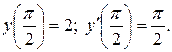
Подставим начальные условия в общее решение 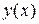и его производную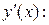

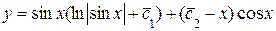
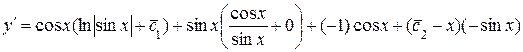
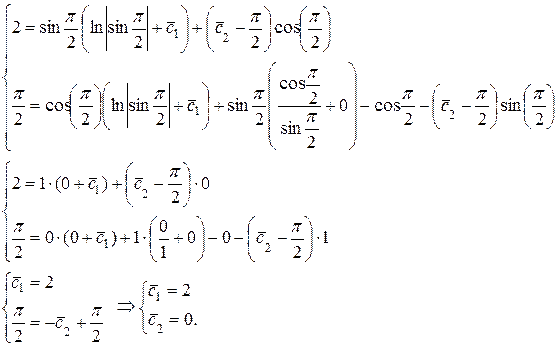
Найденные значения 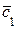и 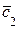при их подстановке в общее решение дают частное решение ЛНДУ:

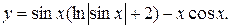
Ответ: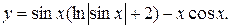

Примеры

Решить дифференциальное уравнение методом вариации произвольных постоянных:

1.

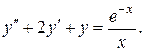
2.

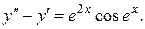
3.

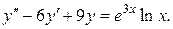
4.

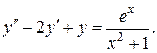
5.

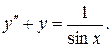
6.

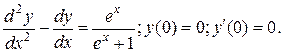
Решить дифференциальное уравнение методом неопределенных коэффициентов:

7.

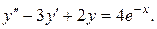
8.

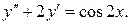
9.

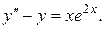
10.

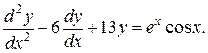
11.

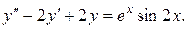
12.

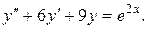
13.

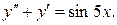
14.

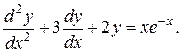
15.

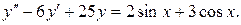
16.

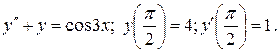
17.

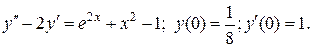
18.

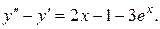
19.

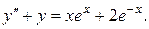
20.

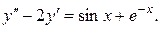
21.

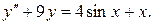
Ответы

1.

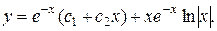
2.

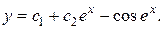
3.

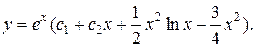
4.

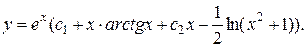
5.

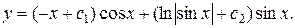
6.

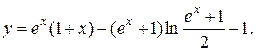
7.

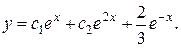
8.

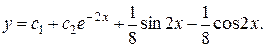
9.

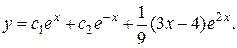
10.

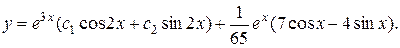
11.

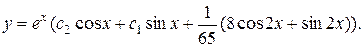
12.

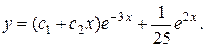
13.

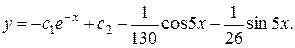
14.

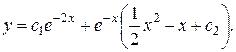
15.

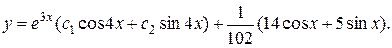
16.

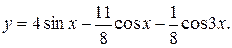
17.

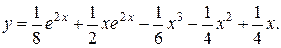
18.

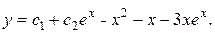
19.

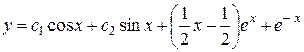
20.

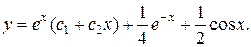
21.

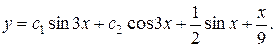
§4. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами

Основные понятия

Определение 1.Уравнение вида:

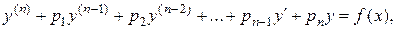(1)

где 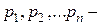заданные действительные числа, 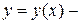неизвестная функция, ее производные до n-го порядка включительно,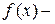

непрерывная на промежутке 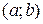функция, называется линейным дифференциальным уравнением (ЛДУ) n-го порядка.

Если 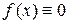для всех 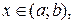то уравнение (1) называется линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка, соответствующим уравнению (1). Такое уравнение имеет вид:

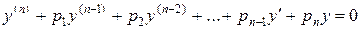. (2)

Для нахождения общего решения ЛОДУ достаточно найти n линейно независимых на промежутке 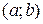решений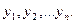

Определение 2.Функции 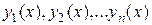на промежутке 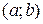называются линейно независимыми, если тождество:

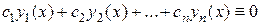
для всех 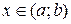может выполняться только при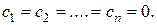

Такую систему линейно независимых решений ЛОДУ называют фундаментальной.

Если найдена фундаментальная система решений 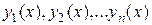ЛОДУ, то общее решение этого уравнения записывается в виде:

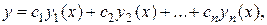
где 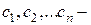произвольные постоянные.

Общее решение ЛНДУ (1) задается формулой:

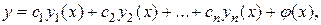
где 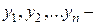фундаментальная система решений соответствующего ЛОДУ (2), 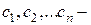произвольные постоянные, 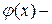некоторое частное решение ЛНДУ (1).

2. ЛОДУ n-го порядка с постоянными коэффициентами

Рассмотрим уравнение (2):

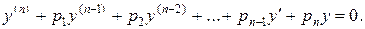
Его характеристическое уравнение имеет вид:

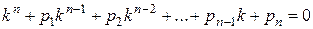(3)

Рассмотрим возможные случаи, возникающие при решении уравнения (3).

1) Все корни уравнения (3) действительные и различные, обозначим их 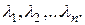Тогда фундаментальную систему решений ЛОДУ составят функции:

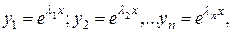
а общее решение этого уравнения имеет вид:

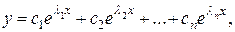
где 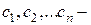произвольные постоянные.

2) Все корни характеристического уравнения (3) различны, но среди них имеется комплексный корень 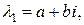тогда 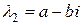тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых решений:

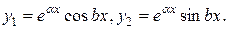
Записав линейно независимые решения ЛОДУ (2), соответствующие всем корням уравнения (3), получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными даст общее решение уравнения (2).

3) Среди корней характеристического уравнения имеются кратные корни. Пусть 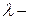действительный 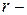кратный корень. Тогда ему соответствует 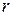линейно независимых решений вида: 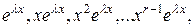а в формуле общего решения будут слагаемые вида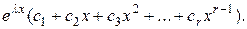

4) Если 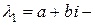комплексный корень характеристического уравнения (3) кратности 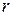, то ему и сопряженному с ним корню 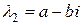той же кратности 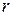соответствуют 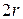линейно независимых решений вида:

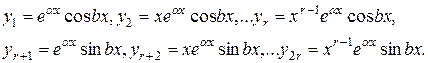
Записав линейно независимые решения ЛОДУ (2), соответствующие всем простым и кратным корням уравнения (3), получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными даст общее решение уравнения (2).

3. ЛНДУ n-го порядка с постоянными коэффициентами

Для получения частного решения 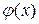ЛНДУ (1) используют два метода.

1) Метод вариации произвольных постоянных

Пусть дано уравнение (1):

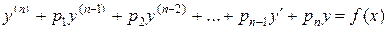
и общее решение соответствующего ЛОДУ (2):

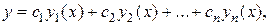
Функцию 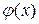ищем в виде:

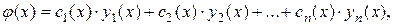
Для нахождения 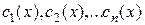составим систему уравнений:

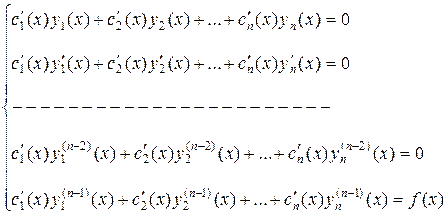
И решая ее, получим 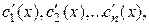а затем, интегрируя, находим 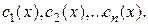Следовательно, частным решением ЛНДУ будет функция:

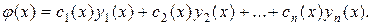
Значит, общим решением ЛНДУ является:

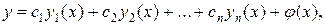
где 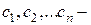произвольные постоянные.

2) Метод неопределенных коэффициентов

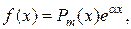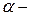а) Пусть где действительное число, 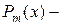многочлен 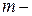ой степени ,

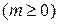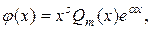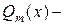Тогда где многочлен степени 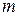с неопределенными коэффициентами, число 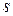равно кратности числа 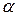как корня характеристического уравнения (3).

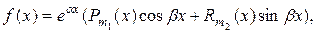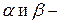б) Пусть где действительные числа, 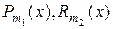– многочлены степени 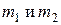соответственно.

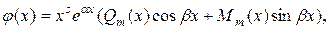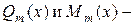Тогда где многочлены степени 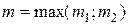с неопределенными коэффициентами, 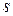равно кратности числа 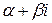как корня характеристического уравнения (3).

Замечание 1. Коэффициенты многочленов 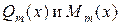находят методом неопределенных коэффициентов.

Замечание 2. Если в уравнении (1) функция 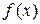равна сумме нескольких функций 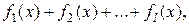то его частное решение строится так: 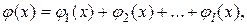где 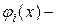частное решение ЛНДУ с правой частью, равной .

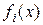Примеры с решениями

Пример 1. Решить уравнение:

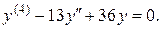
Решение. Это ЛОДУ четвертого порядка. Его характеристическое уравнение имеет вид:

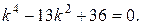
Уравнение является биквадратным. Выполним замену: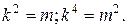

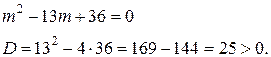
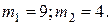
Следовательно, корнями характеристического уравнения являются числа:

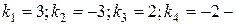действительные и различные.

Значит, функции 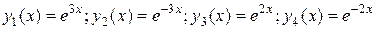составляют фундаментальную систему решений данного уравнения. Поэтому общее решение можно записать в виде:

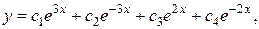
где 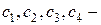произвольные постоянные.

Ответ: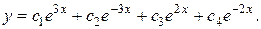

Пример 2. Решить уравнение:

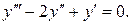
Решение. Это ЛОДУ третьего порядка. Его характеристическое уравнение имеет вид:

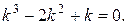
Решим его:

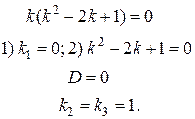
Следовательно, корнями характеристического уравнения являются числа:

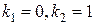кратности 2.

Значит, функции 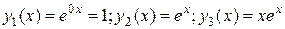составляют фундаментальную систему решений данного уравнения. Поэтому общее решение можно записать в виде:

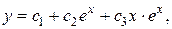
где 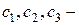произвольные постоянные.

Ответ: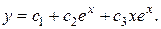

Пример 3. Решить уравнение:

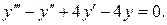
Решение. Это ЛОДУ третьего порядка. Его характеристическое уравнение имеет вид:

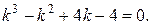
Для решения этого уравнения выполним разложение его левой части на множители:

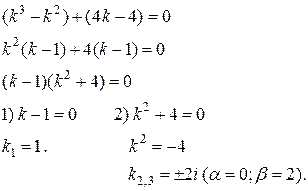
Следовательно, корнями характеристического уравнения являются числа:

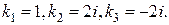
Значит, функции 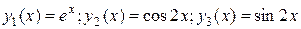составляют фундаментальную систему решений данного уравнения. Поэтому общее решение можно записать в виде:

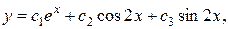
где 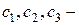произвольные постоянные.

Ответ: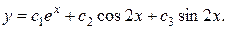

Пример 4. Решить задачу Коши:

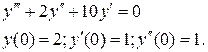
Решение. Это ЛОДУ третьего порядка. Его характеристическое уравнение имеет вид:

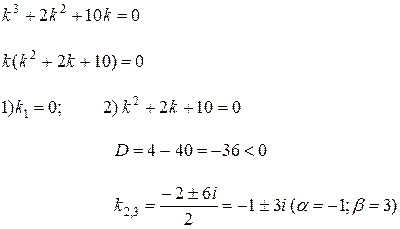
Следовательно, корнями характеристического уравнения являются числа:

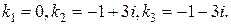
Значит, функции 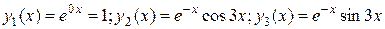составляют фундаментальную систему решений данного уравнения. Поэтому общее решение можно записать в виде:

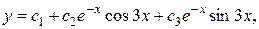
где 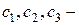произвольные постоянные.

Теперь найдем значения 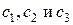такими, чтобы полученное при этих значениях из общего решения частное решение удовлетворяло заданным начальным условиям:

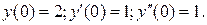
Получим предварительно 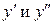из общего решения:

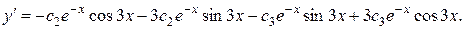
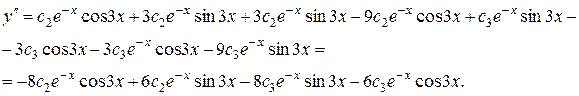
Составим систему уравнений относительно 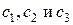, подставляя в 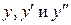значения: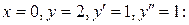

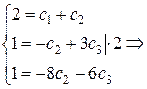
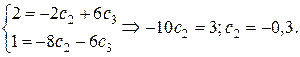
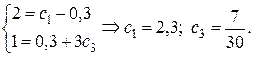
Следовательно, частное решение данного ЛОДУ, удовлетворяющее заданным начальным условиям, задается функцией:

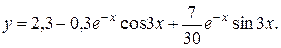
Ответ: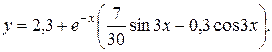

Пример 5. Решить уравнение:

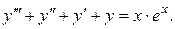
Решение. Это ЛНДУ третьего порядка.

1) Решим соответствующее ЛОДУ:

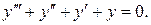
Его характеристическое уравнение имеет вид:

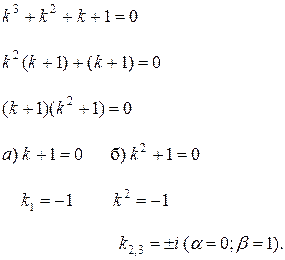
Следовательно, корнями характеристического уравнения являются числа:

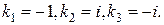
Значит, функции 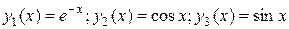составляют фундаментальную систему решений ЛОДУ. Поэтому общее решение ЛОДУ можно записать в виде:

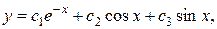
где 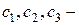произвольные постоянные.

2) Найдем частное решение 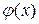данного ЛНДУ. Правая часть 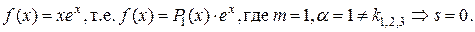Поэтому частное решение ищем в виде:

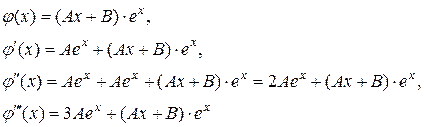
Подставим 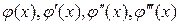в данное уравнение вместо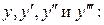

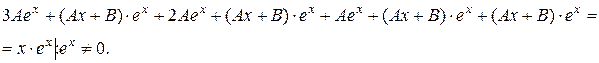
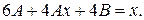
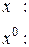
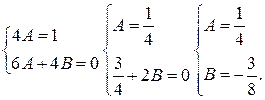
Отсюда следует, что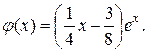

3) Запишем общее решение данного ЛНДУ:

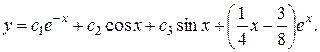
Ответ: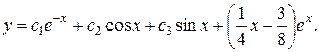

Примеры

Решить уравнения и задачи Коши

1.

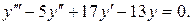
2.

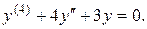
3.

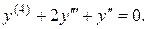
4.

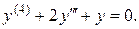
5.

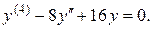
6.

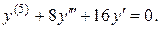
7.

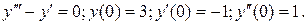
8.

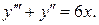
9.

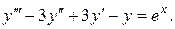
10.

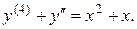
11.

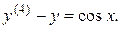
12.

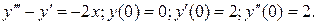
13.

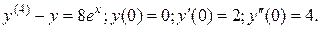
14.

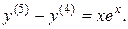
Ответы

1.