Тема 10. Выбор в условиях неопределенности и риска.
7.
8.
9.
10.
10.1. Для каких функций полезности потребитель расположен к риску, безразличен к риску, отвергает риск (если W - благосостояние)? Вычислите абсолютный и относительный коэффициенты неприятия риска Эрроу-Пратта:
а) 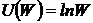 ; в)
; в) 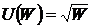 ; д)
; д) 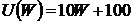 ; ж)
; ж) 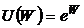 ;
;
б) 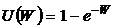 ; г)
; г) 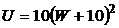 ; е)
; е) 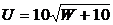 ; з)
; з) 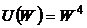 .
.
10.2. Студенту Удачникову предлагают сыграть в кости. Если выпадает число от единицы до трех, то он должен отдать $100. Если выпадет число от четырех до шести, то он получит $100. Его благосостояние оценивается в $200. Сыграет ли Удачников в кости, если известно, что он:
а) любитель риска, б) отвергает риск?
10.3. Студенту Покеровскому предлагают карточную игру. Колода состоит из 36 карт. Если выпадает “картинка” (валет, дама, король, туз), то Покеровский получает выигрыш $100. Если выпадает другая карта, то он должен заплатить 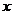 долларов.
долларов.
а) Чему должно быть равно х, чтобы игра была справедливой?
б) Чему должно быть равно х в случае, если колода состоит из 52 карт?
10.4. Имеются два варианта поведения водителя при нарушении правил дорожного движения:
первый - подчиниться командам инспектора и заплатить штраф 80 руб.;
второй - скрыться с места нарушения, тогда с вероятностью 0.1 водитель будет задержан и оштрафован на 800 рублей, а с вероятностью 0.9 останется безнаказанным.
Доход водителя равен 2000рублей в месяц. Определите, какой вариант он выберет, если функция полезности водителя:
а) 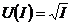 , б)
, б) 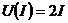 , в)
, в) 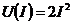 .
.
10.5. Потребитель имеет дом стоимостью $40 000. Вероятность пожара составляет 1%. При какой максимальной цене потребитель установит пожарную сигнализацию, которая предотвращает пожар, если:
а) функция полезности потребителя 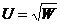 , ( где W - благосостояние);
, ( где W - благосостояние);
б) функция полезности потребителя 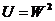 ;
;
в) зависит ли макс. цена сигнализации от степени приверженности к риску?
10.6. Функция полезности потребителя равна 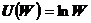 , где W - благосостояние. Начальное благосостояние $10. При участии в лотерее потребитель, с равными шансами, может выиграть или проиграть $5.
, где W - благосостояние. Начальное благосостояние $10. При участии в лотерее потребитель, с равными шансами, может выиграть или проиграть $5.
а) Определите премию за риск и безрисковый эквивалент лотереи.
б) Как изменится величина премии за риск, если начальное благосостояние возрастает до $100?
в) Определите величину премии за риск и безрискового эквивалента лотереи, если 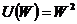 и начальное благосостояние: $10, $100.
и начальное благосостояние: $10, $100.
10.7. Покеровскому снова предлагают карточную игру. Колода состоит из 36карт. Если выпадает туз, то Покеровский получает выигрыш $20. В противном случае он должен заплатить $2.5. Функция полезности 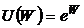 , где W - благосостояние. Начальное благосостояние оценивается величиной $10. Определите:
, где W - благосостояние. Начальное благосостояние оценивается величиной $10. Определите:
а) Согласится ли Покеровский на игру?
б) Сколько он согласен заплатить за участие в игре в случае положительного ответа на предыдущий вопрос?
в) Как изменится ответ при функции полезности 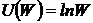 ?
?
10.8. Функция полезности студента Страхова 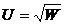 , где W - его благосостояние. Страхову предлагают купить лотерейный билет по цене $2. Билет с вероятностью 0.001 позволяет выиграть $10 000 и с вероятностью 0.999 является проигрышным. Начальное благосостояние равно $100. Купит ли Страхов билет? Сколько он согласен заплатить за билет?
, где W - его благосостояние. Страхову предлагают купить лотерейный билет по цене $2. Билет с вероятностью 0.001 позволяет выиграть $10 000 и с вероятностью 0.999 является проигрышным. Начальное благосостояние равно $100. Купит ли Страхов билет? Сколько он согласен заплатить за билет?
10.9. Студент Страхов нашел лотерейный билет, который с вероятностью 0.1 принесет выигрыш $100 и с вероятностью 0.9 является безвыигрышным. Функция полезности студента 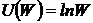 , где W- благосостояние. Начальное благосостояние равно $20. По какой цене x студент согласится продать билет?
, где W- благосостояние. Начальное благосостояние равно $20. По какой цене x студент согласится продать билет?
10.10. Автолюбитель имеет машину стоимостью в $9000. Вероятность угона автомобиля составляет 0.1%. (В случае угона благосостояние автолюбителя составит $1– это стоимость брелка на ключах, оставшихся от автомобиля.) Страховая компания предлагает застраховать машину от угона, заплатив $10. В случае наступления страхового случая потребитель получает $9000. Определите:
а) согласится ли автолюбитель на предлагаемую страховку, если он безразличен к риску?
б) какую сумму х согласится заплатить автолюбитель за предлагаемую страховку, если он имеет функцию полезности 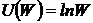 ?
?
10.11. Фермер рассматривает три варианта транспортировки яиц из курятника в дом:
первый - отнести в дом все 24 яйца за один раз,
второй - отнести в дом 12 яиц и затем вернуться за остальными,
третий - перенести яйца за три раза по 8 яиц.
При транспортировке вероятность того, что фермер упадет и разобьет все яйца, составляет величину 1/12. Сколько яиц будет перенесено целыми и невредимыми при каждом варианте? Определить стандартное отклонение для каждого случая. Является ли данный пример подтверждением поговорки “не клади все яйца в одну корзину”?
10.12. Определите ожидаемый доход и стандартное отклонение для двух ценных бумаг, если известно, что для первой ценной бумаги
| Вероятность | 0,1 | 0,5 | 0,2 | 0,2 |
| Доход | –500 |
а для второй ценной бумаги
| Вероятность | 0,2 | 0,2 | 0,4 | 0,1 | 0,1 |
| Доход | –200 |
Определите:
а) Каков будет выбор безразличного к риску инвестора?
б) Каков будет выбор отвергающего риск инвестора?
10.13. Каждый доллар, инвестированный в проект А, превращается в 2 доллара без всякой случайности. Каждый доллар, инвестированный в проект В, с вероятностью 0.5 превращается в 6 долларов и с вероятностью 0.5 обращается в ноль. Инвестор имеет 1000 долларов, которые может использовать в сумме S для инвестиций в проект А, а в сумме (1000 – S) для инвестиций в проект В. Определите:
а) Какую минимальную сумму S необходимо инвестировать проект А, чтобы он стал более выгодным, чем проект В?
б) Какова оптимальная величина S для потребителя, если его функция полезности 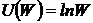 ?
?
в) Какова оптимальная величина S для потребителя, если его функция полезности 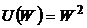 ? Почему?
? Почему?
10.14. Постройте карты кривых безразличия для потребителей, имеющих функции полезности:
а) 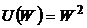 ; б)
; б) 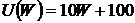 ; в)
; в) 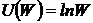 ; г)
; г) 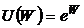 ,
,
если доход W - случайная величина, принимающая значения W1 и W2 с вероятностями p1 и p2 .
10.15. Удачников имеет $100 и ему вновь предлагают сыграть в кости. Если выпадет единица, он проиграет x долларов. Если выпадет другое число, он получит 3x долларов. Покажите на графике:
а) бюджетное ограничение Удачникова;
б) кривые безразличия, если Удачников расположен к риску или не любит риск.
10.16. Студентка Петрова учится экономике. После окончания учебы она устроится на работу, с вероятностью 0.5 ее заработная плата будет составлять $1600, а с вероятностью 0.5 будет равна $2500. Функция полезности Петровой: 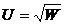 , где W - денежный доход. Определите и покажите на рисунке:
, где W - денежный доход. Определите и покажите на рисунке:
а) кривые безразличия;
б) величину безрискового эквивалента и премию за риск;
в) страховку от низкооплачиваемой работы, которую согласна заплатить Петрова.
10.17. Функция полезности потребителя: 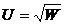 , начальное богатство: W0 = 100. С вероятностью ρ = 0.4 у потребителя могут похитить имущество на сумму L = 80. Страховая компания предлагает приобрести страховку с коэффициентом страхового покрытия γ = 0.2. Определите:
, начальное богатство: W0 = 100. С вероятностью ρ = 0.4 у потребителя могут похитить имущество на сумму L = 80. Страховая компания предлагает приобрести страховку с коэффициентом страхового покрытия γ = 0.2. Определите:
а) На какую сумму застрахует свое имущество потребитель (какой размер страхового покрытия выберет)? Верно ли, что он выберет полную страховку?
б) Покажите на графике точку оптимума потребителя.
в) Как изменятся ответы на пп. a)-б), если коэффициент страхового покрытия составит γ = 0.4?
г) Выгодно ли страховой компании увеличить значение коэффициента страхового покрытия γ? Почему?
[1] См. Пиндайк Р.С., Рубинфельд Д.Л. Микроэкономика. Гл. 3.
[2] Чеканский А.Н., Фролова Н.М. Теория спроса, предложения и рыночных структур. Гл. 3.
[3] См. М.Кац, Х.Роузен «Микроэкономика», гл.5.
[4] См. Х. Вэриан «Микроэкономика: промежуточный уровень», гл.9.9.
