Тема 11. Обоснование решений в процессе управления запасами
План
1. Принятие решений без использования численных вероятностей исходов.
2. Максимаксное и максиминное решение.
3. Критерий Гурвица.
4. Принятие решений с использованием численных значений вероятностей исходов.
Краткое содержание темы
Максимаксное решение – это максимизация максимума возможных доходов. Максиминное решение – это максимизация минимума возможных доходов.
Рассмотрим пример 1. Владелец небольшого магазина в начале каждого дня закупает для реализации некий скоропортящийся продукт по цене 50 рублей за единицу. Цена реализации этого продукта – 60 рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1, 2, 3 или 4 единицы. Если продукт за день не продан, то в конце дня его всегда покупают по цене 30 рублей за единицу. Сколько единиц этого продукта должен закупать владелец каждый день руководствуясь правилом максимакса и правилом максимина?
Поясним, как заполняется таблица 44.
Таблица 44 – Возможные доходы за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| -10 | -30 | -50 | ||
| -20 | ||||
| максимакс | ||||
| максимин | -10 | -30 | -50 |
В клетке (2,2) для реализации было закуплено 2 единицы, спрос был 2 единицы. Поэтому возможный доход для этой клетки: 60x2 (реализация двух единиц) – 50x2 (их предварительная закупка) = 20.
В клетке (3,1) была закуплена для реализации 1 единица, спрос был 3 единицы. Поэтому возможный доход для этой клетки: 60x1 (реализация только одной единицы, владелец магазина неверно оценил спрос) – 50x1 (ее предварительная закупка) = 10.
В клетке (3,4) было закуплено для реализации 4 единицы, спрос был 3 единицы. Поэтому возможный доход для этой клетки 60x3 (реализация трех единиц, на которые был спрос) – 50x4 (предварительная закупка четырех единиц) + 30(4 - 3) (реализация в конце дня непроданной единицы) = 10. И т. д.
Каждая реализованная в течение дня единица приносит доход 60 - 50 = 10, а каждая реализованная в конце дня единица приносит доход 30 - 50 = -20 (то есть убыток).
Рассматриваемые способы принятия решения состоят в следующем. В каждом столбце (то есть для каждого возможного решения) находим максимальное число. Это числа 10, 20, 30, 40 соответственно. Запишем их в строке «максимакс» и найдем среди них максимальное. Это 40, что соответствует решению о закупке для реализации 4 единиц. Руководствуясь правилом максимакса, каждый раз надо закупать для реализации 4 единицы. Это – подход очень азартного человека.
В каждом столбце (то есть для каждого возможного решения) находим минимальное число. Это числа 10, -10, -30, -50 соответственно. Запишем их в строке «максимин» и найдем среди них максимальное. Это 10, что соответствует решению о закупке для реализации 1 единицы. Руководствуясь правилом максимина, каждый раз надо закупать для реализации 1 единицу. Это – подход очень осторожного человека.
Минимаксное решение – это минимизация максимума возможных потерь, причем упущенная выгода также трактуется как потери. Пример 2. Вернемся к предыдущему примеру. Таблица возможных потерь за день имеет следующий вид (таблица 45). Поясним, как заполняется таблица 45.
В клетке (2,2) было закуплено для реализации 2 единицы, спрос был 2 единицы, то есть число закупленных для реализации единиц равно спросу за день. Поэтому возможные потери для этой клетки равны нулю.
В клетке (3,1) закупленная для реализации единица продана, но могли бы продать еще 3 – 1 = 2 единицы, заработав на их продаже 2*(60 – 50) = 20. Это и есть возможные потери.
Таблица 45 – Возможные потери за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| минимакс |
В клетке (3,4) одна закупленная единица не реализована в течение дня. Она приносит убыток 1*(50 – 30) = 20. Это и есть возможные потери.
В каждом столбце (то есть для каждого возможного решения) находим максимальное число. Это числа 30, 20, 40, 60 соответственно. Запишем их в строке «минимакс» и найдем среди них минимальное. Это 20, что соответствует решению о закупке для реализации 2 единиц. Руководствуясь правилом минимакса, каждый раз надо закупать для реализации 2 единицы.
Критерий Гурвица – это компромиссный способ принятия решений. Составляется таблица возможных доходов (см. пример 1). Задаются числа a и b, называемые весами. Условия на a и b:
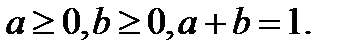
Для каждого возможного решения определяются наименьший и наибольший возможные доходы и вычисляется целевая функция по правилу:
a*(наименьший доход) + b*(наибольший доход).
Выбираем решение, при котором целевая функция принимает наибольшее значение.
Веса a и b выбирает сам исследователь. При a=0, b=1 получаем правило максимакса. При a=1, b=0 получаем правило максимина.
Пример 3. Вернемся к примеру 1. Зададим a=0,4 и b=0,6. a+b=0,4+0,6=1.
Из таблицы возможных доходов (таблица 44) для каждого решения находим наименьший и наибольший возможные доходы (это числа в строках «максимакс» и «максимин»). Заполним таблицу 46.
Числа во 2-м и 3-м столбцах взяты из таблицы возможных доходов. Числа 3-го столбца умножаем на a=0,4 и результат пишем в 4-м столбце.
Таблица 46 - Возможные доходы за день с учетом критерия Гурвица
| Возможные решения | Наибольший доход | Наименьший доход | а х (наименьший доход) | b х (наибольший доход) | Сумма |
| 0,4*10=4 | 0,6*10=6 | 4+6=10 | |||
| -10 | 0,4*(-10)=-4 | 0,6*20=12 | -4+12=8 | ||
| -30 | 0,4*(-30)=-12 | 0,6*30=18 | -12+18=6 | ||
| -50 | 0,4*(-50)=-20 | 0,6*40=24 | -20+24=4 |
Числа 2-го столбца умножаем на b=0,6 и результат пишем в 5-м столбце. В 6-м столбце находится сумма соответствующих элементов 4-го и 5-го столбцов. Находим максимум в 6-м столбце (это 10). Он соответствует возможному решению о закупке для реализации одной единицы.
Критерий Гурвица необходим для того, чтобы лицо, принимающее решение, обратило внимание и на самую лучшую, и на самую худшую отдачу от конкретной стратегии и определило субъективную вероятность для каждой из них.
Правило максимальной вероятности. Пример 4.Модифицируем пример. 1. Пусть известно, что на практике спрос 1 наблюдался 15 раз спрос 2 наблюдался 30 раз, спрос 3 наблюдался 30 раз, спрос 4 наблюдался 25 раз, то есть известна частота каждого возможного исхода.
Всего наблюдений было 15 + 30 + 30 + 25 = 100. Отношением частоты исхода к сумме частот всех исходов определим вероятность каждого исхода. Составим таблицу 47. Находим исходы, вероятность которых максимальна. Это 2 и 3.
Таблица 47 – Данные для использования правила максимальной вероятности.
| Возможные исходы | Сумма | ||||
| Частота | |||||
| Вероятность, p | 15/100=0,15 | 30/100=0,30 | 30/100=0,30 | 25/100=0,25 |
В таблице 44 возможных доходов наибольший возможный доход из этих двух решений у решения «закупать 3 единицы» (30 против 20). Поэтому, руководствуясь правилом максимальной вероятности, надо закупать для реализации 3 единицы [1, с. 61-65].
Задачи
Задача 23. Владелец небольшого магазина в начале каждого дня закупает для реализации некий скоропортящийся продукт по цене 80 рублей за единицу. Цена реализации этого продукта – 110 рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1, 2, 3 или 4 единицы. Если продукт за день не продан, то в конце дня его всегда покупают по цене 55 рублей за единицу. Сколько единиц этого продукта должен закупать владелец каждый день руководствуясь правилом максимакса и правилом максимина? Решение оформите в таблице 48.
Таблица 48 – Возможные доходы за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| максимакс | ||||
| максимин |
Задача 24. Владелец небольшого магазина в начале каждого дня закупает для реализации некий скоропортящийся продукт по цене 80 рублей за единицу. Цена реализации этого продукта – 110 рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1, 2, 3 или 4 единицы. Если продукт за день не продан, то в конце дня его всегда покупают по цене 55 рублей за единицу. Сколько единиц этого продукта должен закупать владелец каждый день руководствуясь правилом минимакса? Решение оформите в таблице 49.
Таблица 49 – Возможные потери за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| минимакс |
Задача 25. Владелец небольшого магазина в начале каждого дня закупает для реализации некий скоропортящийся продукт по цене 80 рублей за единицу. Цена реализации этого продукта – 110 рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1, 2, 3 или 4 единицы. Если продукт за день не продан, то в конце дня его всегда покупают по цене 55 рублей за единицу. Сколько единиц этого продукта должен закупать владелец каждый день руководствуясь Критерием Гурвица, если a=0,4 и b=0,6? Решение оформите в таблице 50 и 51.
Таблица 50 – Возможные доходы за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| максимакс | ||||
| максимин |
Таблица 51 - Возможные доходы за день с учетом критерия Гурвица
| Возможные решения | Наибольший доход | Наименьший доход | а х (наименьший доход) | b х (наибольший доход) | Сумма |
Задача 26. Владелец небольшого магазина в начале каждого дня закупает для реализации некий скоропортящийся продукт по цене 80 рублей за единицу. Цена реализации этого продукта – 110 рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1, 2, 3 или 4 единицы. Известно, что на практике спрос 1 наблюдался 16 раз, спрос 2 наблюдался 30 раз, спрос 3 наблюдался 30 раз, спрос 4 наблюдался 24 раза. Если продукт за день не продан, то в конце дня его всегда покупают по цене 55 рублей за единицу. Сколько единиц этого продукта должен закупать владелец каждый день руководствуясь правилом максимальной вероятности? Решение оформите в таблице 52 и 53.
Таблица 52 – Возможные доходы за день
| Возможные исходы: спрос в день | Возможные решения: число закупленных для реализации единиц | |||
| максимакс | ||||
| максимин |
Таблица 53 – Данные для использования правила максимальной вероятности.
| Возможные исходы | Сумма | ||||
| Частота | |||||
| Вероятность, p |
