Исследование цепи из последовательно соединенных резистивн0г0, индуктивного и емкостного элементов при синусоидальном токе

Цель работы:

1.Научиться определять основные соотношения электрических параметров цепи из последовательно соединенных элементов с помощью векторных диаграмм.

2.Уяснить особенности резонанса напряжений.

Основные теоретические положения

В цепях синусоидального тока при последовательном соедине­нии идеальных элементов R , I , С второй закон Кирхгофа спра­ведлив для действующих значений падений напряжений в векторной форме.

__ __ __ __

U = UR + UL + UC

Действующие значения нап­ряжений определяется по закону Ома: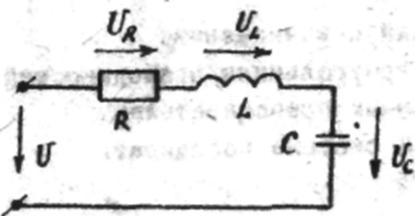

Рис.1

UR = IR ; UL=IxL ; UC=IxC ;

Построение векторной диаграммы начинается с вектора тока, общего для всех элементов цепи. При сложении векторов каждый

последующий вектор располагается вслед за предыдущим с учетом сдвига фаз между током и напря­жением для каждого элемен­та (рис.2).

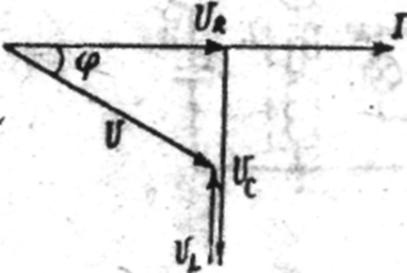
Рис.2

Из точки 0 строим вектор тока произ­вольного направления (например, горизонтально). Вектор напряжения UR строим из точки 0 совпадающим с вектором тока. К концу вектора UR пристраиваем вектор UC , отстающий от вектора тока на 90° (вниз). Далее вектор напряжения U_L строим опе­режающим вектор тока на 90°. Соединяем начало первого вектора с концом последнего, получаем результирующий вектор приложенного к цепи напряжения U. При UL >UC вектор напряжения опережает вектор тока I, угол φ считается положительным. При U_L < UC век­тор U отстает от тока на угол φ. Угол φ считается отрицатель­ным. Цепь носит активно-емкостный характер.

Если UL=UC, вектор напряжения U совпадает с вектором UR по направлению и по величине. Цепь носит чисто активный ха­рактер. Это явление называется резонансом напряжений.

Реальная катушка индуктивности обладает достаточно большим активным сопротивлением, пренебречь которым нельзя. Поэтому угол сдвига фаз между током и напряжением катушки не равен 90°. Его можно определить, подключив катушку к источнику и измерить U_К, I_К, P_К.

φк=arcos P_К/ U_К I_К

При построении векторной диаграммы вектор sin φк напряжения U_К можно строить опережающим вектор тока на угол φк , или разло­жить его на две составлявшие U_АК и UL

U_АК= U_К sin φк, где U_К - падение напряжения на катушке.

Векторная диаграмма для случая, когда UL < UC имеет

вид (рис.3). В результате построения векторной диаграммы необходимо удостове­риться, что полученный век­тор напряжения

U численно равен поданному напряжению в цепь, а φ соответ-ствует расчетному значению.

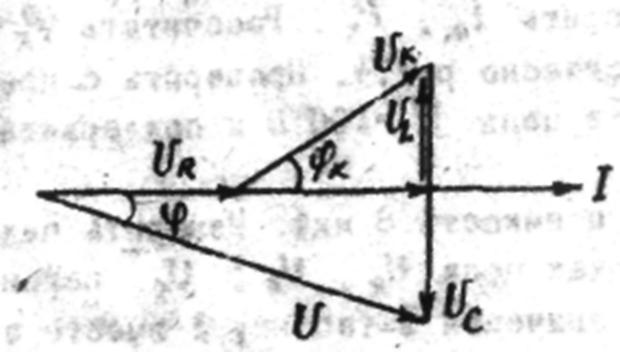
Рис.3

Из треугольника напряжений (рис.2) можно получить треугольник сопротивлений, если все сто­роны разделить на

ток I. Он во всех элементах один и тот же. Если же стороны треугольника напряжений умножить на ток, получим треугольник мощностей.

Из треугольников имеем следующие соотношения:

R = Z cosφ; X = Z sin φ; P=S cosφ; Q = S sin φ.

Перечень приборов и оборудования

1.Лабораторный автотрансформатор (ЛАТР).

2.Комплект измерительных приборов К-50.

3.Реостат ламповый (активный потребитель).

4.Катушка индуктивности.

5.Магазин емкостей.

6.Вольтметр с пределом 150 В.

Порядок выполнения работы

1.Ознакомиться с приборами и оборудованием, записать их харак­теристики в бланк отчета.

2.Подключить к источнику питания через комплект измерительных приборов К-50 одну катушку индуктивности. Показать схему пре­подавателю.

3.Подать на катушку 100 В, измерить I_К, Р_К . Рассчитать φ_К .

4.Собрать электрическую цепь согласно рис.4. Проверить с препо­давателем. Подать напряжение в цепь U=100 В и поддерживать его постоянным.

Включить одну лампу, катушку и емкость 8 мкФ. Измерить паде­ние напряжения на всех элементах цепи UR, UL, UC перенос­ным вольтметром и занести их значения в таблицу 1 вместе с по­казаниями остальных приборов.

Табл.1

Повторить измерения всех параметров , изменяя емкость через 4 мкФ от 8 мкФ до 32 мкФ.По данным таблицы определить режим, близкий к резонансу напряжений.Ему будет соответствовать максимальное значение тока и потребляемой мощности от источника Величины емкости мкФ	Измерено	Вычислено
U	I	Р	UR,	UК	UC	Z	Rа	X	cosφ
В	А	Вт	В	В	В	Ом	Ом	Ом	-

5. Повторить измерения при включенных двух лампах лампового реостата. Данные внести в таблицу 1. Убедиться, что резонанс напряжений наступает при том же значении емкости С_рез

6. Построить векторные диаграммы для трех значений емкости

С<С_рез, С=С_рез >, С>С_рез

для одной или двух ламп по зада­нию преподавателя.

Вычислить основные параметры цепи:

1.Полное сопротивление цепи Z=U/I;

2.Активное сопротивление цепи R_a =R+R_К; ______

3.Реактивное сопротивление X = XL –XC = √ Z - R_a ; 4.Коэффициент мощности cosφ = P / UI

Содержание отчета

1.Технические данные приборов и оборудования.

2.Схема электрической цепи.

3.Расчетные формулы.

4.Таблицы с результатами измерений и вычислений.

5.Векторные диаграммы напряжений, треугольники сопротивлений и мощностей.

6.Графики зависимостей I =f(C) , Z =f(C) , U_K = f(C) , UC = f(C) , cosφ = f(с) в одной системе координат.

7.Краткие выводы по экспериментальным и расчетным данным.

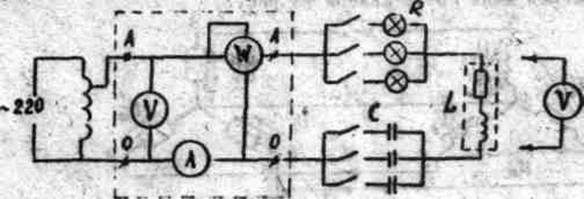
Рис.4

Лабораторная работа № 5

ИССЛЕДОВАНИЕ СИСТЕМЫ ТРЕХФАЗНОГО ТОКА ПРИ СОЕДИНЕНИЙ ПОТРЕБИТЕЛЕЙ "ЗВЕЗДОЙ"

Цель работы:

Проверить опытным путём соотношение между фазными и линейны­ми напряжениями. Уяснить роль нулевого провода. Научиться строить векторные диаграммы напряжений и токов трехфазных цепей. Проана­лизировать с помощью векторных диаграмм изменение фазных напря­жений при наличии и отсутствии нулевого провода.

Основные теоретические положения

В цепях трехфазного тока всегда действует симметричная сис­тема трехфазной э.д.с. Независимо от способа соединения обмоток генератора систему напряжений, им вырабатываемых, можно предста­вить векторной диаграммой (рис.1). Если пренебречь сопротивлени­ем проводов линии и потерями нап­ряжений в ней, можно считать, что непосредственно на потребители воздействует эта же симметричная система линейных напряжений. Ре­жимы работы потребителей сущест­венно зависят от способа их соеди- нения и характера самих потребителей.

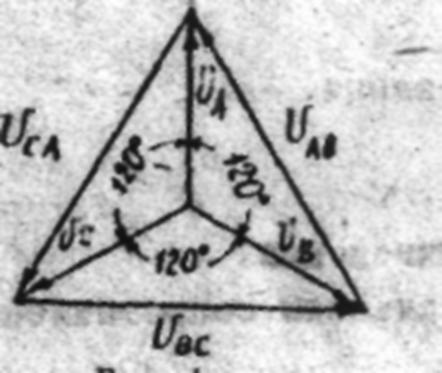
Рис 1.

1.Соединение потребителей "звездой" с нулевым проводом.

Электрическая цепь представлена на рис.2.

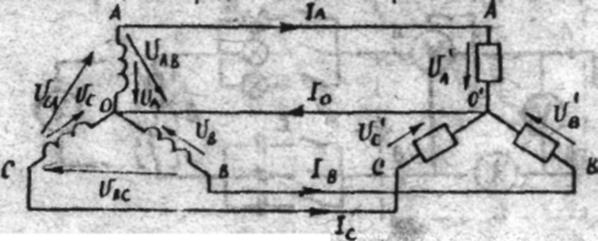
Рис.2

При наличии нулевого провода фазные напряжения на потребителе остается неизменными и равными фазным напряжениям генерато­ра.

UА = U’А, UВ = U’В, UС = U’С при любых видах нагрузки.

Измерив фазные и линейные напряжения на потребителях и ли­нейные токи (Iл = Iф ) помощью векторных диаграмм можно прове­рить выполнение первого закона Кирхгофа в трехфазных цепях:

Построение векторных диаграмм проводится следующим образом. Строится симметричная система фазных и линейных напряжений (см. рис.1). Поскольку потребители, используемые в работе, является активными, фазные токи откладывается в масштабе по направление фазных напряжений. Затем находится их векторная сумма. Результи­рующий вектор должен в масштабе соответствовать измеренному то­ку I₀ . Принцип построения остается неизменным во всех вариан­тах нагрузки.

Симметричной в трехфазной системе считается такая нагрузка, при которой, потребители трех фаз является одинаковыми по харак­теру и по величине, т.е.

ZА=ZВ=ZС; φА=φв=φС

Если хотя бы одно из этих условий не соблюдается, нагрузка яв­ляется несимметричной.

Пример построения векторной диаграммы для несимметричной нагрузки представлен на рис.3.

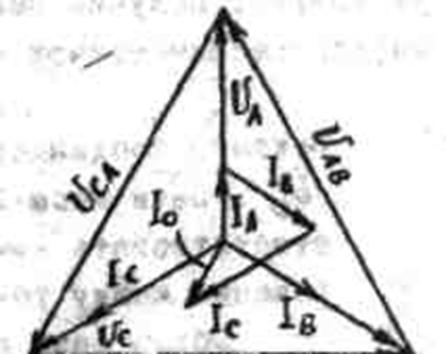
Рис.3

2. Соединение потребителей "звездой" в трехпроводной системе.

При симметричной нагрузке в четырехпроводной линии ток в
нулевом проводе отсутствует. Если этот провод отсоединить,

ре­жим работы потребителей не изменится. Фазные напряжения на пот­ребителях U_A', U_B' , U_C' останутся одинаковыми по величине, как и токи I_A, I_B , I_C. Поэтому векторная диаграмма напряжений и токов в трехпроводной системе совпадает с векторной диаграммой в четырехпроводной системе.

При несимметричной нагрузке фазные напряжения на потребите­ле могут отличаться от одноименных фазных напряжений на генера­торе и в общем случае образует несимметричную систему векторов. Из-за отсутствия нулевого провода потенциал нулевой точки потре­бителей 0' не будет равным нулю. Однако остаются справедливыми соотношения:

__ __ __ __ __ __ __ __ __

U_AВ = U_A'- U_B', U_BС = U_B '- U_C' , U_CА =U_C' - U_A'

Положение нулевой точки 0' на векторной диаграмме можно найти следующим образом.

Измеряются фазные и линейные напряжения на потребителе и U₀ между нулевыми точками потребителя и генера­тора. Начинается построение векторной диаграммы с построения симметричной системы векторов фазных и линейных напряжений гене­ратора (см.рис.1). Далее из вершин треугольника А,В,С раствором циркуля, равным соответственно U_A', U_B', U_C' делаем засечки. Точка их пересечения соответствует потенциалу точки 0'. Соеди­нив точку 0' с вершинами треугольника, получим напряжения U_A', U_B', U_C'. Векторная диаграмма для несимметрич-ной нагрузки пред­ставлена на рис.4.

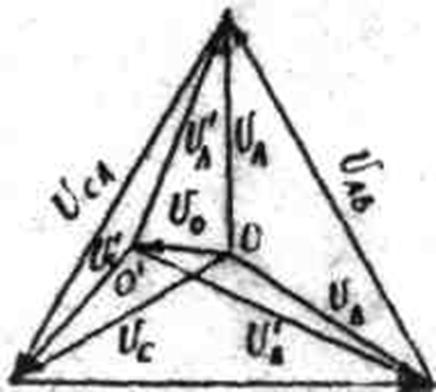
Рис.4.

Вектор, соединявший точки 00' есть U₀ . Он в масштабе должен со­ответствовать измеренному нап­ряжении между точками 00'.

Обрыв фазы и короткое за­мыкание в фазе потребителя мож­но считать несимметричной наг­рузкой и векторные диаграммы строить по принципу, описанно­му выше. Если но фазным напря-

жениям отложить фазные токи и найти их векторную сумму, можно убедиться, что при любой нагрузке

__ __ __

IA + IB + IC = 0.

Порядок выполнения работы

1.Ознакомиться с приборами и оборудованием и записать их техни­ческие данные в бланк отчета.

2.Собрать электрическую цепь согласно приложенной схеме. Прове­рить правильность её сборки с преподавателем.

3.Провести измерения токов и напряжений при различных режимах нагрузки согласно таблице 1, куда внести результаты измерений.

Таблица 1

Режим работы

Измерить

U12

U23

U31

U1

U2

U3

U0

I1

I2

I3

I0

В

В

В

В

В

В

В

А

А

А

А

Четырехпроводная система

1.Симметричная нагрузка 2.Несимметрич-ная нагрузка 3. Обрыв фазы при симметрич- ной нагруз­ке

Трехпроводная система

1.Симметричная нагрузка 2.Несимметрич-ная нагрузка 3. Обрыв фазы при симметрич- ной нагруз­ке 4.Короткое замыкание фазы при симметричной нагрузке

.

Режимы нагрузки:

1.Симметричная нагрузка: количество потребителей во всех фазах одинаково.

2.Несимметричная нагрузка: в одной фазе три потребителя, во вто­рой - два, в третьей - один.

3.Обрыв фазы имитируется отключением всех потребителей в одной фазе при симметричной нагрузке в двух других.

4.Короткое замыкание в одной фазе выполняется соединением нача­ла и конца этой фазы проводником при симметричной нагрузке в двух других фазах.

Содержание отчета

1.Технические характеристики всех измерительных приборов.

2.Схема электрической цепи.

3.Результаты измерений.

4.Векторные диаграммы напряжений и токов для всех режимов нагрузки.

5.Краткие выводы по работе.

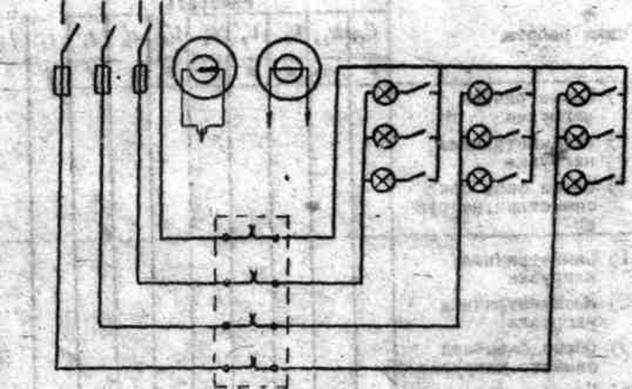
Схема исследования трехфазной системы при соединении потребителей "звездой"

Лабораторная paбота №6

ИССЛЕДОВАНИЕ СИСТЕМЫ ТРЕХФАЗНОГО ТОКА ПРИ СОЕДИНЕНИИ ПОТРЕБИТЕЛЕЙ "ТРЕУГОЛЬНИКОМ"

Цель работы:

Проверить опытным путем соотношения между фазными и линей­ными токами при симметричной нагрузке. Научиться строить вектор­ные диаграммы токов и напряжений при соединении потребителей "треугольником".

Основные теоретические положения

При соединении потребителей треугольником каждая фаза потре- бителя находится под линейным напряжением, поэтому в этом случае Uф=Uл (рис.1).

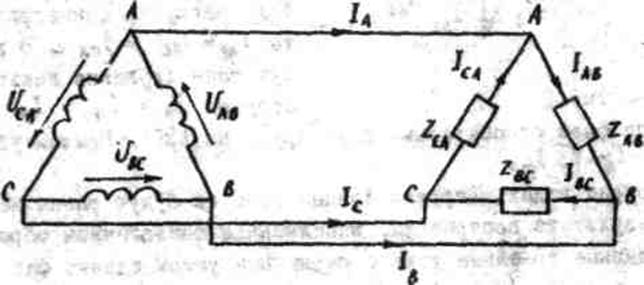
Рис.1

Соотношения между линейными (в линейных проводах) и фазны­ми (в фазах потребителя) токами в соответствии с 1 законом Кирх­гофа можно представить как

__ __ __

IА = IАВ - IСА

__ __ __

IВ= IВС - IАВ

__ __ __

IС = IАВ - IВС

В общем случае фазные токи сдвинуты относительно фазных напряжений на углы φАВ, φВС и φСА, величины которых определяются характером нагрузки φАВ = φВС =φСА=0.

Зная величину фазных токов, линейные токи можно определить с по­мощью векторных диаграмм следующим образом. Линейные напряжения, вырабатываемые генератором и поступающие на потребителя, можно, изображать в виде "треугольника", как и при соединении "звездой". Но для удобства построения и наглядности их можно представить и в виде симметричной звезды (рис.2).

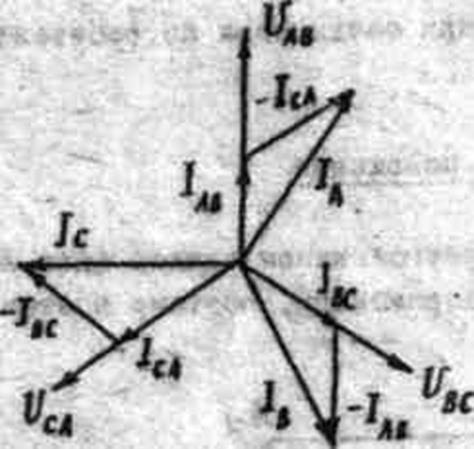
Рис.2

Фазные токи IАВ, IВС, IСА строим совпадающими с нап­ряжениями UАВ, UВС, UСА Далее, используя правило сложения векторов, находим линейные токи; Надо помнить, что вычитание вектора соот­ветствует сложение вектора, равного ему по величине и
обратного по направлению.
Если нагрузка симметричная, то IАВ = IВС = IСА
В ре­зультате сложения векторов получим IА = IВ = IС,

сдвинутые по фазе относительно друг друга на 120°. Причем убе­димся, что Iл =√3 Iф .

При других видах нагрузки фазные токи не будут равны между
собой. В результате построений, выполненных аналогичным образом, получим неравные линейные токи с различным углом сдвига фаг меж­ду ними.

Приборы и оборудование

1.Вольтметр переменного напряжения (150 В).

2.Амперметр переменного тока (5 А).

3.Ламповые реостаты.

Порядок выполнения работы

1.Ознакомиться с приборами и оборудованием и записать их техни­ческие данные в бланк отчета.

2.Собрать электрическую цепь согласно приложенной схемы.

Проверить правильность ее сборки с преподавателем.

3.Провести измерение токов и напряжений при режимах нагрузки, указанных, в таблице 1, куда внести результаты измерений.

Таблица 1

Режимы работы	Измерить
U12	U23	U31	I12	I23	I31	I1	I2	I3
В	В	В	А	А	А	А	А	А
1.Симметричная нагрузка 2.Несимметричная нагрузка 3.0брыв фазы при симметричной нагрузке 4.Обрыв линейного провода при сим­метричной нагрузке

Режимы нагрузки:

1.Симметричная нагрузка: количество потребителей во всех фазах одинаково.

2.Несимметрична: нагрузка: в одной фазе включены три потребите­ля, в другой - два, в третьей - одни.

3.Обрыв фазы: в одной фазе вое потребители отклонены, в двух других симметричная нагрузка.

4.Обрыв линейного провода: отключить от потребителя и источни­ка один из линейных проводов при симметричной нагрузке фаз потребителя.

Содержание отчета

1.Технические характеристики измерительных приборов.

2.Схема электрической цепи.

3.Результаты измерений.

4.Векторные диаграммы напряжений и токов для всех режимов нагрузки.

5.Краткие выводы.

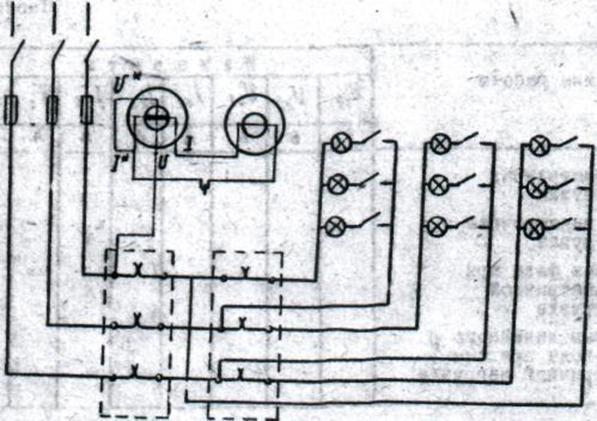
Схема исследования трехфазной системы при соединении потребителей "треугольником"

Лабораторная работа № 7