С позиций менеджмента качества процессы экспертного оценивания следует отнести к так называемым «специальным».
Методические указания
к выполнению курсового проекта:
Экспертные методы в инвестиционно-строительной и эксплуатационной деятельности
Утверждено
редакционно-издательским советом университета
«____» ____________2016г.
САМАРА 2016
Содержание
Введение.. 3
Практические ситуации: 6
1. Анализ рисков нового строительного проекта и выбора проектной организации.. 6
2. Метод анализа экспертных мнений с помощью дерева решений.. 12
3. Метод анализа с помощью комбинированных методов.. 21
4. Принятие решений в условиях определенности и неопределенности 24
СПИСОК ЛИТЕРАТУРЫ... 47
Задание по вариантам... 48
Введение
Методы экспертных - комплексы психологических и математических процедурполучения от специалистов-экспертов информации о рисках, ее анализа и обобщения (консолидации) с целью выработки рациональных решений.
С позиций менеджмента качества процессы экспертного оценивания следует отнести к так называемым «специальным».
Специальный процесс – это процесс, в котором подтверждение соответствия конечной продукции затруднено и экономически нецелесообразно.
По результатам процессов экспертного оценивания нельзя сразу оценить объективность, обоснованность и точность экспертной оценки.
Принципы современного менеджмента качества позволяют обеспечить все контролируемые условия (критические факторы), необходимые для получения качественной экспертной оценки.
С этой целью необходимо предпринять следующие меры для обеспечения качества экспертных оценок:
1. 
Определить цели и задачи экспертного оценивания.
2. 
Использовать квалифицированных экспертов.
3. 
Применять методы экспертного оценивания, которые являются адекватными с точки зрения контекста риск-менеджмента.
 |
4. Применять адекватную методику обработки, анализа и интерпретации результатов экспертного оценивания.
 |
5. Регистрировать данные, полученные в результате экспертного оценивания.
6. При изменении политики и целей – повторно осуществить мероприятия по пунктам 1-5.
Практические ситуации:
Задание №1.
Руководство строительной инжиниринговой компании приняло решение о привлечении группы внешних экспертов для анализа рисков нового строительного проекта и выбора проектной организации. Допустим (условно), что по результатам отбора кандидатов в эксперты качественным методом было выбрано четыре эксперта с одинаковыми или очень близкими параметрами соответствия заявленным критериям отбора. Зачетная численность экспертной группы: четыре человека.
Итак, четырем кандидатам (
=4) было предложено проранжировать 6 критериев (
=6) выбора проектной компании:
– стоимость разработки проектно-сметной документации;
– минимальный срок разработки;
– опыт компании при проектировании аналогичных строительных объектов;
– репутация на рынке проектной организации;
– объем выполненных работ за предыдущий год;
– текущее финансовое состояние организации.
Наиболее важному критерию присваивается 1-й ранг, наименее важному 6-й.
По результатам ранжирования определены:
- матрица–строка 1-го эксперта 
;
- матрица–строка 2-го эксперта 
;
- матрица–строка 3-го эксперта 
;
- матрица–строка 4-го эксперта 
.
Решение.
Данные запишем в общую матрицу ранжирования.
Таблица 1
Общая матрица ранжирования
 - № эксперта |  | |||||
| | | | | | | |
| Сумма: |
Далее используя формулы 3, 4 получим таблицу средних значений рангов.
Таблица 2
Средние значения рангов
| Ранги | Обозначение критерия | |||||
| | ||||||
| | | | | | | |
| Сумма рангов | ||||||
| Среднее значение | 1,5 | 2,25 | 2,5 | 5,5 | 5,25 |
Далее составляем по формуле 5 матрицу отклонений мнений экспертов от среднего мнения:
Далее используем формулы 6 - 9, получим, суммарное отклонение мнений -того эксперта по всем критериям, суммарное отклонение мнений всех экспертов по всем критериям, а также среднее отклонение мнений -того эксперта от среднего мнения группы по всем критериям.
Таблица 3
Отклонения по всем критериям
| Номер эксперта (первоначальный) | ||||
| Среднее отклонение | 2,5 | 4,5 | ||
| Суммарное отклонение мнений всех экспертов по всем критериям | 2,67 | |||
| Модуль частного отклонения | 0,17 | 2,33 | 1,83 | 1,33 |
Применив формулу 10, получаем матрицу-строку модулей частных отклонений:
Таким образом, кортеж отклонений даст изменение номеров экспертов:
Отсюда следует, что эксперт, имеющий новый номер i=4, может быть исключен из состава экспертной группы, так как его мнения наиболее удалены от среднего мнения.
Задание №2.
Главный экономист предприятия (ЛПР) анализирует планы развития производства на следующий год. Предприятие выпускает, помимо прочего, изделие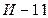 
. Его выпускают в течение длительного срока и реализуют потребителям без всяких затруднений. В плане развития предусматривается перейти к выпуску более современных изделий, чем 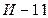. Предлагается два варианта новых моделе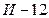й: 
и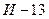 
. Из них последняя является более современной.
Предварительные расчеты показывают, что переход на выпуск модели 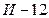принесет за год чистой прибыли на 20 млн. больше, чем выпуск 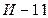(в случае, если реализация новой модели будет удачной). Если реализация новой модели будет идти с затруднениями, то ее производство снизит годовую прибыль на 2 млн. Аналогичные расчеты, произведенные по модели 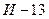, дали такие результаты: при удачном исходе - увеличение прибыли на 30 млн., при неудачном исходе - уменьшение прибыли на 15 млн.
Исходя из знания производственных условий предприятия и рыночной ситуации, ЛПР уверено в успехе на 70%.
ЛПР известно, что существует маркетинговая организация, которая занимается исследованиями в области прогнозирования ситуаций, связанных с модернизацией продукции и выводом ее на рынок. Подобное исследование для данного предприятия будет стоить 300 тыс. Из прошлого опыта известно, что заключения данной организации оказывались верными в 60% случаев, когда предсказывался успех, и в 80% случаев, когда предсказывалась неудача.
Нужно принять решения:
- стоит ли обращаться к услугам маркетингового агентства?
- переходить ли на выпуск нового изделия или продолжать выпускать старую?
- если переходить, то какую модель предпочесть?
Данная задача довольно сложная, поскольку имеется несколько возможных вариантов принятия решений, а также много неупорядоченной информации, вероятностного характера.
Решение.
Для решения подобного рода задач строят дерево решений, которое помогает точно сформулировать проблему и организовать поиск оптимального решения.
Дерево решений, построенное для условий рассматриваемого примера, представлено на рис.1. На рисунке приняты следующие условные обозначения:
- 
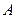- начальное состояние;
- 
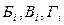- состояния или точки ветвления;
- 
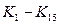- конечные состояния;
- 
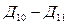- действия первого уровня;
- 
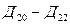- действия второго уровня;
- 
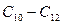- события первого уровня;
- 
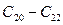- события второго уровня .
Анализируя дерево процедуры принятия решений, несложно заметить, что оно включает ветви двух видов:
- действия, которые зависят от решения ЛПР (закажет оно анализ или нет, какие модели изделия будет рекомендовать к выпуску в следующем году);
- события, которые являются последствиями решений ЛПР, однако на характер которых он не может повлиять (после принятия решения о выпуске нового изделия, успех или неудача с его реализацией не зависят от ЛПР, нельзя также повлиять на характер заключения маркетингового агентства).
На рис. 1 показаны все возможные действия и их последствия, т.е. логическая структура задачи.
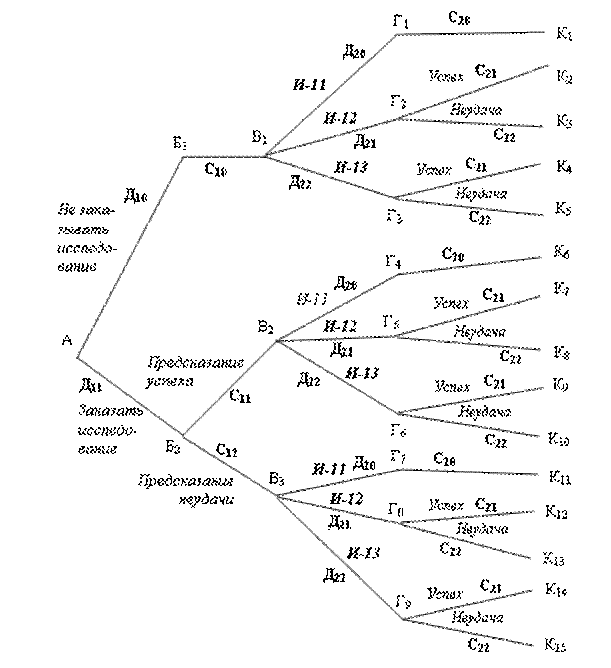
Рис.1. Логическая структура задачи
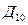- действия, заключающиеся в том, что исследования заказаны не будут.
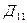- действия, заключающиеся в заказе исследований маркетинговому агентству.
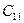- события, заключающиеся в предсказании успеха.
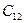- события, заключающиеся в предсказании неудачи.
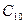- фиктивное событие, введенное для выравнивания числа ветвей.
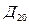- действия заключающиеся в продолжении выпуска изделия .
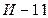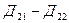- действия, заключающиеся в переходе, соответственно, на модель 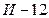и .
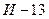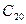- событие, заключающееся в рыночном успехе продолжения выпуска изделия .
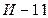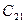- событие, заключающееся в успехе перехода на выпуск одной из новых моделей.
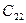- событие, заключающееся в неудаче перехода на выпуск одной из новых моделей.
Однако на основании данного дерева мы не можем сказать, какое из возможных решений будет более рациональным. Для этого требуется дополнить дерево числовыми данными рис.2.
В приведенных выше данных имеются только сравнительные данные. Например, при успешном переходе на выпуск модели 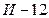дополнительная прибыль составит 20 млн. в год. Рассчитаем изменения в размерах прибыли на основании имеющихся в нашем распоряжении данных:
- «0» - если продолжать выпуск изделия ;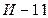
- «+20» - если перейти на выпуск модели 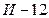и она получит успех на рынке;
- «-2» - если модель 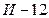будет не востребована потребителями;
- «+30» - если осуществится успешный переход на выпуск модели ;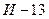
- «-15» - если переход на выпуск модели 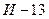будет неудачным.
Известно также, что исследование маркетингового агентства обойдется в 300 тыс. Результаты подсчета алгебраических сумм этих величин записаны справа от вершин дерева на рис. 2.
Теперь, оценить различные варианты действий. Из рисунка видно, что переход на выпуск изделий 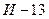по сравнению с переходом на выпуск изделий 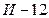является более рискованным. Однако, с другой стороны, модель 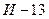дает большую прибыль, чем модель 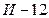. А может быть целесообразнее продолжать выпускать изделие 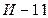? При получении ответа на эти вопросы следует учесть вероятности.
Данная задача решалась бы весьма просто, если было бы точно известно, какое из событи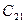й или 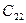произойдет. Однако это неизвестно. В условиях задачи говорится, что ЛПР на 70% уверено в успехе перехода на выпуск одной из новых моделей изделия. То есть вероятность благоприятного исхода в этом случае 
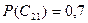. Поскольку 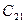и 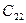составляют полную систему событий, то 
.
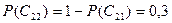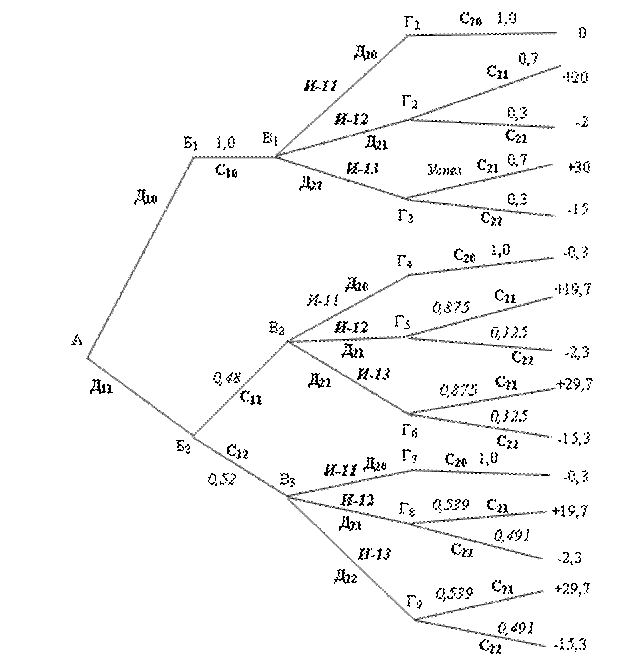
Рис. 2. Схема алгоритма решения
Эти субъективные вероятности, известные до принятия решения, являются априорными. Если ЛПР закажет исследование маркетинговому агентству, то оно учтет его результаты в своем заключении, т. е. первоначальные вероятност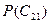и 
и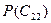 
будут уточнены. То есть будет внесена поправка, учитывающая как характер прогноза (предсказания) маркетингового агентства, так и его точность. Это можно оценить вполне объективно, поскольку известно, насколько прогнозы аналитиков оправдывались, когда они прогнозировали успешный исход, и насколько, когда они прогнозировали неудачу.
Исходя из имеющихся статистических данных, действительно успешное выведение новых товаров на рынок теми производителями, которые заказывали маркетинговое исследование, в 60% случаев предварительно предсказывалось маркетинговым агентством. Или вероятность того, что свидетельство подтверждающее успех имело место при успешном выведении нового товара на рынок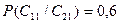 
. А так как 
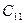(свидетельство, подтверждающее успех) и 
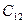(свидетельство, подтверждающее неудачу) составляют полную систему событий, то следует, что 
.
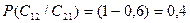Аналогичным образом, вероятность того, что свидетельство подтверждающее неудачу имело место при провале (неудаче) выведения нового товара на рынок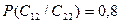 
. И соответственно 
.
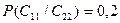Эти данные будут влиять на первоначальные субъективные оценки.
Эти и заданные в условиях вероятности показаны на рис. 2 (прямой шрифт). При этом вероятности фиктивных событий принимаем равными 1,0, т.е.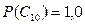 
и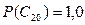 
(чтобы не влиять на результаты расчетов).
Получению заключений маркетингового агентства на дереве решений рис. 2 соответствуют действие 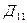и события 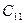или .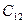
Рассчитаем апостериорные вероятности событи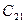й и 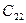с учетом результатов заключений маркетингового агентства ( 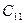и ).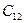
Для расчетов используем вторую форму записи формулы Байеса 14.
Вероятность успеха при предсказании успеха:
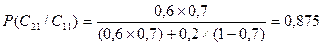(15).
Вероятность неудачи при предсказании успеха:
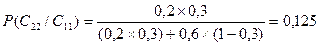(16).
Вероятность успеха при предсказании неудачи:
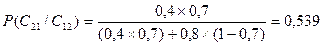(17).
Вероятность неудачи при предсказании неудачи:
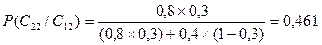(18).
Далее рассчитаем вероятности предсказания успеха и неудач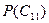и 
и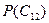 
. Для этого разрешим уравнение Байеса (первую форму записи, см. уравнение 14) относительно 
:
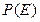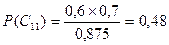(19).
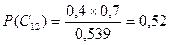(20).
Обозначим вычисленные вероятности на соответствующих ветвях дерева решений на рис. 2 (показано курсивом).
Алгоритм нахождения оптимального решения имеет следующий вид:
1. Для каждого состояния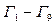 
(см. рис.1) вычисляем значения ожидаемых величин: 
; 
; 
; 
; 
; 
; 
; 
; 
.
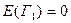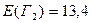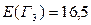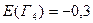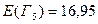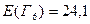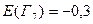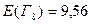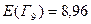Пример расчета для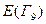 
: 
.
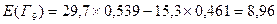2. Для каждого состояния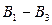 
(см. рис. 1) выберем ветвь 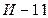, 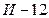или 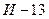, к которой относится максимальный ожидаемый прирост прибыли: 
; 
; 
.
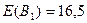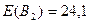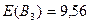3. В каждом состоянии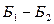 
(см. рис. 1) вычислим максимальный ожидаемый прирост прибыли: 
; 
.
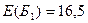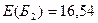4. Находясь в исходном состоянии 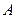, выберем такую ветвь, к которой относится максимальный ожидаемый результат.
Таким образом, опираясь на результаты приведенного выше анализа, оптимальная стратегия поведения главного экономиста выглядит следующим образом.
Заказать исследование аналитикам и если:
- заключение благоприятно, то принять решение о выпуске модели ;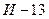
- неблагоприятно, то принять решение о выпуске модели .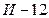
Задание №3
Инвестор планирует получить от объекта недвижимости прибыль в размере 2 500. Однако он полагает, что в результате воздействия конкретных причин: 
, 
, 
, 
, 
, оцененных им по 5-балльной системе баллами - 
: 2, 1, 3, 4, 5, возможны убытки 
в размере 300, 180, 250, 150, 190. соответственно. Рассчитать вероятность появления убытка и возможные потери.
Таблица 4
Исходные данные, к заданию №4 в табличной форме
| Планируемая прибыль | | |  | |  | |  | |  | |
| 2 500 |
Решение задания .
Фактор риска 
- потери планируемого дохода. На основе указанной в условии информации совокупные потери в результате возникновения причин составят:
(21).
Определим долю потерь прибыли по каждой причине:
(22).
Так, например, по причине :
(23).
Результаты расчетов занесены в стр. 3 таблице 7.
Рассчитаем вероятность влияния каждой причины на фактор 
(см. таблицу 7):
(24).
где 
- балл влияния -й причины на фактор 
, 
.
(25).
(26).
(27).
Результаты расчетов представлены в стр. 4 таблицы 5.
Правила расчета остальных показателей приведены в таблице 5.
Таблица 5
Расчет потерь инвестора в результате воздействия конкретных причин на планируемый доход
| Код строки | Причина |  | | | | |
| Влияние на фактор, баллы | ||||||
| Потери | ||||||
| Доля потерь в совокупных потерях | 0,2804 | 0,1682 | 0,2336 | 0,1402 | 0,1776 | |
| Вероятность появления причины | 0,1333 | 0,0667 | 0,2 | 0,2667 | 0,3333 | |
| Средневзвешенная потеря | 84,112 | 30,280 | 58,411 | 21,028 | 33,738 | |
Вероятность потери дохода по причине  | 0,0374 | 0,0112 | 0,0467 | 0,0374 | 0,0592 |
Вероятность потери дохода в результате воздействия всех причин равна 0,1919.
Средняя величина потерь в результате воздействия причин 227,57.
Вывод к заданию №3.
В результате воздействия перечисленных причин инвестор может недополучить от объекта недвижимости около 227,57 т. е. размер прогнозируемой прибыли уменьшится до 2 272,43.
Вероятность потери прибыли 19,19%.
Задание №4.
Используя данные задания № 4, определить интервал изменения среднего размера потерь и область риска, дать оценку качеству полученных результатов.
Решение задания №4.
Для оценки интервала размера потерь и качества расчетного уровня риска 19,19% рассчитаем показатели: среднее отклонение, среднеквадратическое отклонение, коэффициент вариации. Результаты расчетов приведены в таблице 6.
Средняя величина потери прибыли:
(28).
Таблица 6
Расчет интервалов изменения потери прибыли и риска потери
| Причина | | | | | |
Потери  | |||||
Вероятность появления причины,  | 0,1333 | 0,0667 | 0,2 | 0,2667 | 0,3333 |
Линейное отклонение потери по -й причине от среднего  | -34 | -64 | -24 | ||
Квадратное отклонение  | 7 396 | 1 156 | 1 296 | 4 096 | |
 | 986,13 | 77,07 | 259,20 | 1092,27 | 192,00 |
Суммарное значение:
(29).
Среднеквадратичное отклонение:
(30).
Нижняя граница интервала потерь:
(31).
Верхняя граница интервала потерь:
(32).
Таким образом, интервал изменения средней потери прибыли: от 162,94 до 265,06.
Для определения, является ли расчетная средняя величина фактора риска достаточно объективной для анализируемых данных, воспользуемся коэффициентом вариации:
(33).
По расчетным данным значение коэффициента вариации:
(34).
Вывод к заданию №4.
Расчеты среднего уровня риска и потерь по анализируемым данным являются достаточно объективными, так как значение коэффициента вариации 
. Совокупность данных, характеризующих причины потерь, является однородной, размер потерь имеет невысокую степень изменения.
Подгруппа студентов выступает в качестве экспертов, оценивая уровень развития воли пяти студентов группы (они не входят в экспертную группу) по 5-бальной шкале:
- 1 балл - никогда не проявляет волевые качества,
- 2 балла - довольно редко проявляет волевые качества,
- 3 балла - иногда проявляет волевые качества,
- 4 балла - часто проявляет волевые качества,
- 5 баллов - всегда проявляет волевые качества.
Определить уровень согласованности мнений.
Вариант «Г» предпочтительнее.
Нормализация (приведение показателей в одну числовую шкалу)
Таблица 10
Нормализация
| Альтернатива | Критерии | Сумма весов | |||
| Аренда | Площадь | Доступность | Состояние | ||
| А | 1,00 | 0,75 | - | - | 12,5 |
| Б | 0,67 | - | 1,00 | 1,00 | 19,32901 |
| В | 0,33 | 1,00 | 0,75 | 0,33 | 17,07469 |
| Г | - | 0,50 | 0,25 | 0,67 | 8,583333 |
Вариант «Б» предпочтительнее.
2 вариант «при неизвестном значении веса критерия» (условие неопределенности), при абсолютных значениях.
Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(aijpj)
∑(a1,jpj) = 6.34•0.25 + 95•0.25 + 9•0.25 + 7•0.25 = 29.335
∑(a2,jpj) = 8.4•0.25 + 110•0.25 + 5•0.25 + 4•0.25 = 31.85
∑(a3,jpj) = 10.46•0.25 + 90•0.25 + 6•0.25 + 6•0.25 = 28.115
∑(a4,jpj) = 12.51•0.25 + 100•0.25 + 8•0.25 + 5•0.25 = 31.3775
| Ai | П1 | П2 | П3 | П4 | ∑(aijpj) |
| A1 | 1,59 | 23,75 | 2,25 | 1,75 | 29,34 |
| A2 | 2,1 | 27,5 | 1,25 | 31,85 | |
| A3 | 2,62 | 22,5 | 1,5 | 1,5 | 28,12 |
| A4 | 3,13 | 1,25 | 31,38 | ||
| pj | 0,25 | 0,25 | 0,25 | 0,25 |
Выбираем из (29,335; 31,85; 28,115; 31,3775) максимальный элемент max=31,85 Вывод: выбираем стратегию N=2.
Критерий Лапласа.
Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т,е,:
q1 = q2 = ,,, = qn = 1/n,
qi = 1/4
| Ai | П1 | П2 | П3 | П4 | ∑(aij) |
| A1 | 1,59 | 23,75 | 2,25 | 1,75 | 29,34 |
| A2 | 2,1 | 27,5 | 1,25 | 31,85 | |
| A3 | 2,62 | 22,5 | 1,5 | 1,5 | 28,12 |
| A4 | 3,13 | 1,25 | 31,38 | ||
| pj | 0,25 | 0,25 | 0,25 | 0,25 |
Выбираем из (29,34; 31,85; 28,12; 31,38) максимальный элемент max=31,85. Вывод: выбираем стратегию N=2.
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т,е,
a = max(min aij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т,е, этот критерий выражает пессимистическую оценку ситуации,
| Ai | П1 | П2 | П3 | П4 | min(aij) |
| A1 | 6,34 | 6,34 | |||
| A2 | 8,4 | ||||
| A3 | 10,46 | ||||
| A4 | 12,51 |
Выбираем из (6,34; 4; 6; 5) максимальный элемент max=6,34.
Вывод: выбираем стратегию N=1.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т,е, обеспечивается:
a = min(max rij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т,е, этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий, Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы,
1. Рассчитываем 1-й столбец матрицы рисков
r11 = 12,51 - 6,34 = 6,17; r21 = 12,51 - 8,4 = 4,11; r31 = 12,51 - 10,46 = 2,05; r41 = 12,51 - 12,51 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 110 - 95 = 15; r22 = 110 - 110 = 0; r32 = 110 - 90 = 20; r42 = 110 - 100 = 10;
3. Рассчитываем 3-й столбец матрицы рисков,
r13 = 9 - 9 = 0; r23 = 9 - 5 = 4; r33 = 9 - 6 = 3; r43 = 9 - 8 = 1;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 7 - 7 = 0; r24 = 7 - 4 = 3; r34 = 7 - 6 = 1; r44 = 7 - 5 = 2;
| Ai | П1 | П2 | П3 | П4 |
| A1 | 6,17 | |||
| A2 | 4,11 | |||
| A3 | 2,05 | |||
| A4 |
Результаты вычислений оформим в виде таблицы.
| Ai | П1 | П2 | П3 | П4 | max(aij) |
| A1 | 6,17 | ||||
| A2 | 4,11 | 4,11 | |||
| A3 | 2,05 | ||||
| A4 |
Выбираем из (15; 4,11; 20; 10) минимальный элемент min=4,11
Вывод: выбираем стратегию N=2.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма, За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(si),
где si = y min(aij) + (1-y)max(aij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем si,
s1 = 0,5•6,34+(1-0,5)•95 = 50,67
s2 = 0,5•4+(1-0,5)•110 = 57
s3 = 0,5•6+(1-0,5)•90 = 48
s4 = 0,5•5+(1-0,5)•100 = 52,5
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | y min(aij) + (1-y)max(aij) |
| A1 | 6,34 | 6,34 | 50,67 | ||||
| A2 | 8,4 | ||||||
| A3 | 10,46 | ||||||
| A4 | 12,51 | 52,5 |
Выбираем из (50,67; 57; 48; 52,5) максимальный элемент max=57.
Вывод: выбираем стратегию N=2.
Критерий Ходжа-Лемана.
Для каждой строки рассчитываем значение критерия по формуле:
Wi = u∑aijpj + (1 - u)min(a)ij
Рассчитываем Wi,
W1 = 0,5•29,335 + (1-0,5)•6,34 = 17,8375
W2 = 0,5•31,85 + (1-0,5)•4 = 17,925
W3 = 0,5•28,115 + (1-0,5)•6 = 17,0575
W4 = 0,5•31,3775 + (1-0,5)•5 = 18,18875
| Ai | П1 | П2 | П3 | П4 | ∑(aijpj) | min(aj) | Wi |
| A1 | 1,59 | 23,75 | 2,25 | 1,75 | 29,34 | 6,34 | 17,84 |
| A2 | 2,1 | 27,5 | 1,25 | 31,85 | 17,93 | ||
| A3 | 2,62 | 22,5 | 1,5 | 1,5 | 28,12 | 17,06 | |
| A4 | 3,13 | 1,25 | 31,38 | 18,19 | |||
| pj | 0,25 | 0,25 | 0,25 | 0,25 |
Выбираем из (17,84; 17,93; 17,06; 18,19) максимальный элемент max=18,19.
Вывод: выбираем стратегию N=4.
Критерий максимакса.
| Ai | П1 | П2 | П3 | П4 | max(aij) |
Наши рекомендации |