Расчет стропильной системы по первой группе предельных состояний

Расчёт стропильной системы ведём согласно СНБ 5.05.01-2000 “Деревянные конструкции”.

Материал деревянных конструкций – сосна ГОСТ 8486-86. Расчётное сопротивление определяем по формуле:

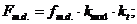(3.1.2)

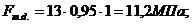
При изгибе с осевым сжатием должно удовлетворяться следующее условие

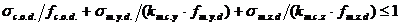; (3.1.3)

где s_с.о.d –расчётное напряжение сжатия, определяемое по формуле

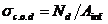; (3.1.4)

f _с.о.d – расчётное сопротивление сжатию

s_m.y.d – расчётные напряжение изгиба, определяемые по формуле:

s_m.i.d=M_i.d/W_i.d; (3.1.5)

M_i.d – расчётный изгибающий момент относительно соответствующей оси

W_i.d – расчётный изгибающий момент сопротивления поперечного сечения элемента относительно соответствующей оси и принимаемый для цельных элементов W_i.d = W_i.inf

k_m.c – коэффициент, учитывающий увеличение напряжений при изгибе по направлению соответствующей оси от действия продольной силы

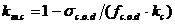; (3.1.6)

k_c – коэффициент продольного изгиба, определяемый по формуле:

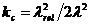; (3.1.7)

Гибкость элементов цельного, постоянного по длине сечения:

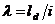; (3.1.8)

где l_d – расчётная длина элемента

l_d =m₀ ∙ l, m=0,73 по таблица 7.1 /10/

i– радиус инерции сечения элемента в направлении действующей оси:

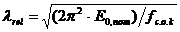; (3.1.9)

Для изгибаемых элементов, не имеющих постоянного подкрепления сжатой кромки из плоскости изгиба, следует также провести проверку на устойчивость плоской формы деформирования

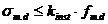; (3.1.10)

где k_inst – коэффициент устойчивости изгибаемых элементов

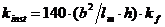; (3.1.11)

b – ширина поперечного сечения

k_f – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l_m , определяемый по таблице 7.4 /10/

h – максимальная высота поперечного сечения на участке l_m

l_m – расстояние между опорными сечениями элемента

Расчёт стропильной системы по второй группе предельных состояний

Предельные прогибы элементов здания не должны превышать величин, указанных в /9/.

Наибольший прогиб элементов постоянного сечения следует определять по формуле:

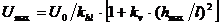; (3.1.12)

где U₀ – прогиб балки постоянного сечения высотой h без учёта деформаций сдвига;

h_max – наибольшая высота сечения;

l – пролёт элемента;

k_h1 – коэффициент, учитывающий влияние переменности высоты сечения, принимаемый равным 1 для элементов постоянного сечения;

k_v – коэффициент, учитывающий влияние деформаций сдвига от поперечной силы.

Значения коэффициентов k_v и k_h1 для основных расчётных схем приведены в таблице 8.2 /10/

Расчёт стропильной системы сводим в таблицу 3.4.3

Таблица 3.1.3 – Результаты расчета

	Стр.нога	Затяжка	Стойка
Дано:	Сжатие+изгиб	Растяжение	Сжатие
M(Н∙мм)	26204000,00	0,00	0,05
N(Н)	9418,00	6016,00	13709,00
f(Mpa)	11,20	11,20	11,20
A расч.(мм^2)	840,89	537,14	1224,02
h(мм)	200,00	125,00	150,00
b(мм)	75,00	50,00	150,00
Aприн.(мм^2)	15000,00	6250,00	22500,00
Мом.ин.(мм^4)	50000000,00	8138020,83	42187500,00
Мом.соп.(мм^3)	500000,00	130208,33	562500,00
i(мм)	57,74	36,08	43,30
L(мм)	8553,00	3871,00	1671,00
ld	6243,69
lm	6360,00
kf	1,13
Гибкость	148,14	107,28	38,59
Kc	0,07	0,13	0,99
Напр.сж.	0,63	0,96	0,61
Пров.устой.	0,76	1,44	11,13
	ИСТИНА	ИСТИНА	ИСТИНА
Напр. Изг.	52,41	-	-
Km,c,	0,17	-	-

Продолжение таблицы 3.1.3

Проверка на изгиб с осевым сжатием
1>(выполн.)	27,82	-	-
Kinst	27983,49	-	-
Устойчивость плоской формы деформирования
1>(выполн.)	0,831	-	-
Проверка прогиба
E(Mpa)	10000,000	-	-
q(Н/мм)	3,729	-	-
u	0,0000000054	-	-
Допустимый прогиб	0,0067	-	-
Пров. Жесткости	ИСТИНА

РАСЧЕТ ПРОСТЕНКА.