Отношения между простыми категорическими суждениями. €

Для анализа простого суждения надо знать те отношения, которые логически допустимы между простыми суждениями.

Простые суждения

Сравнимые несравнимые

Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Например: «Все американские индейцы живут в резервациях»; «Некоторые американские индейцы не живут в резервациях».

Несравнимыми среди простых являются суждения, имеющие различные субъекты или предикаты. Таковы, например, два суждения: «Среди космонавтов есть летчики»; «Среди космонавтов есть женщины».

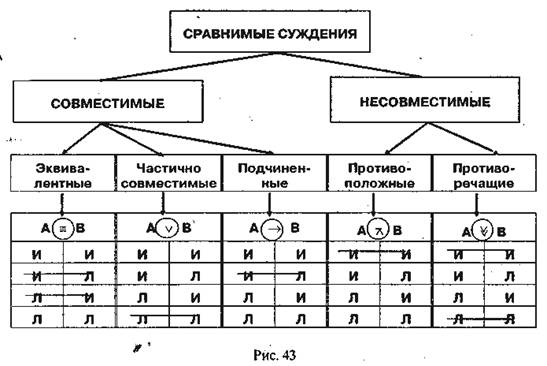
Сравнимые суждения

Совместимые: к совместимым относятся суждения, которые одновременно могут быть истинными.	Несовместимые: несовместимыми являются суждения А и Е, А и О, Е и I, которые одновременно не могут быть истинными.
Виды совместимости	Виды несовместимости Несовместимыми являются суждения А и Е, А и О, Е и I, которые одновременно не могут быть истинными.
Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: субъекты и предикаты, однотипную — утвердительную или отрицательную — связку, одну и ту же выраженную квантором количественную характеристику.	Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными. При ложности одного из них другое будет истинным: Например, при ложности суждения «Некоторые злаки ядовиты» будет истинным суждение «Некоторые злаки не являются ядовитыми». В то же время при истинности одного из частных суждений другое может быть как истинным, так и ложным	Подчинение имеет место между суждениями А и I, Е и О. При истинности общего суждения частное всегда будет истинным: А→I; Е→O. При ложности частного суждения общее суждение также будет ложным: При ложности общего суждения подчиненное частное может быть как истинным, так и ложным. При истинности подчиненного частного общее может быть как истинным, так и ложным.	Противоположными (контрарными) являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными. Истинность одного из противоположных суждений определяет ложность другого. «Все офицеры — военнослужащие» определяет ложность суждения «Ни один офицер не является военнослужащим».	Противоречащими (контрадикторными) являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными. Для противоречия характерна строгая, или альтернативная несовместимость: при истинности одного из суждений другое всегда будет ложным; при ложности первого второе будет истинным. Отношения между такими суждениями регулируются законом исключенного третьего. Если А признается истинным, то О будет ложным (А→О); при истинности Е будет ложным I (Е→┐I). И наоборот: при ложности А будет истинным О (┐А→O); а при ложности Е будет истинным I (┐E→1).

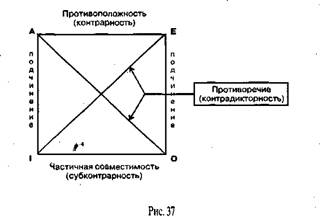
Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом(рис. 37). Его вершины символизируют простые категорические суждения — А, Е, I, О; стороны и диагонали — отношения между суждениями.

Между двумя сравнимыми суждениями возможны следующие отношения:

(1) подчинение,

(2) противоположность (контрарность),

(3) субконтрарность,

(4) противоречие.

Для установления логических значений простых суждений необходимо знать правила, которым подчиняются эти отношения.

Правила подчинения: между А и I, а также Е и О.

· Если А и Е – истинны, то I и О – истинны.

· Если А и Е – ложны, то I и О – неопределенны (истинны или ложны).

· Если I и О – истинны, то А и Е – неопределенны (истинны или ложны).

· Если I и О – ложны, то А и Е – ложны.

Правила контрарности (противоположности): между А и Е.

• Если одно из них – истинно, то другое – ложно.
• Если одно из них – ложно, то другое – неопределенно (истинно или ложно).

Правила субконтрарности (частичной противоположности): между I и О.

• Если одно из них – ложно, то другое – истинно.
• Если одно из них – истинно, то другое – неопределенно (истинно или ложно).

Правила контрадикторности (противоречия): между А и О; Е и I.

• Если одно из них – истинно, то другое – ложно.
• Если одно из них – ложно, то другое – истинно.

Выводы из “логического квадрата”:

1. Контрарные суждения не могут быть одновременно истинными. Это утверждение означает, что общие по количеству и противоположные друг другу по качеству суждения могут быть одновременно ложными («Все студенты – гении» и «Ни один студент не является гением» - оба ложные), но если одно из контрарных суждений истинно, то другое обязательно будет ложным (например, если суждение «Все следователи - юристы» - истинное суждение, то суждение «Ни один следователь не юрист» - ложное).

2. Субконтрарные суждения не могут быть одновременно ложными. Это утверждение означает, что два частных по количеству, но противоположных по качеству суждения могут быть одновременно истинными («Некоторые студенты – гении» и «Некоторые студенты - не гении»), но если одно из суждений ложно, то другое обязательно будет истинным (например, если «Некоторые птицы не имеют крыльев» - ложное суждение, то суждение «Некоторые птицы имеют крылья» будет истинным).

3. Контрадикторные суждения не могут быть одновременно ни истинными, ни ложными. Это правило утверждает, что два сравнимых суждения, отличающиеся друг от друга и качеством и количеством, не могут быть одновременно ни истинными, ни ложными. Например, суждения «Все студенты – гении» и «Некоторые студенты не являются гениями» не могут быть одновременно ни истинными, ни ложными. Если одно из них истинно, то другое обязательно будет ложным.

4. Из истинности подчиняющего общего суждения следует истинность подчиненного ему частного суждения, а из ложности подчиненного частного следует ложность подчиняющего его общего суждения. Это правило утверждает, что сравнимые суждения, одинаковые по качеству, но различные по количеству могут быть одновременно истинными, если истинность частного суждения выводится из истинности его подчиняющего общего суждения (например: если верно, что «Все студенты – грамотные люди», то тогда и суждение «Некоторые студенты являются грамотными людьми» также будет истинным), и могут быть одновременно ложными, если ложность общего суждения выводится из ложности подчиненного ему частного суждения (например: если ложно частное суждение «Некоторые рыбы не живут в воде», то и суждение «Все рыбы не живут в воде» также будет ложным).