Подозрительно простая задача

Задача. Не стальном тросе А висит груз. В плоско­сти, перпендикулярной тросу А, движется трос Б. Как сделать, чтобы трос Б, продолжая движение, не разорвал бы трос А и сам не был бы разорван?

Я оставляю магнитофон и выхожу в коридор. Пусть решают самостоятельно. Устраиваюсь у окна, закуриваю. Докурить мне не удается, зовут в класс.

- Повторите, пожалуйста, условия.
Повторяю.

- И это все?

- Все.

- Тогда задача решена. Мы думали, там есть еще
что-то. Подозрительно простая задача.

Включаю магнитофон:

- Веселая ситуация. Можно показывать в цирке:
трос проходит сквозь трос, а тому хоть бы что... На
грани фантастики.

— Раз ситуация фантастическая, позовем золо­
тую рыбку. Трос А может свободно дойти до троса Б.
Это реальность Р_г А вот остальное - фантастика.

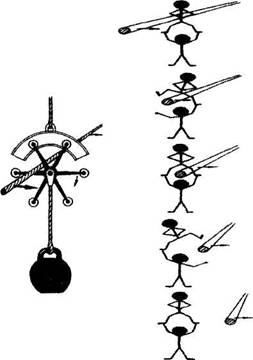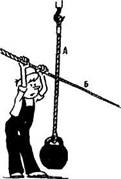
Рис. 5

—Почему? Трос А может частично войти в трос
Б. У троса £ должен быть какой-то запас прочности,
обрыв произойдет не сразу.

—Значит, мы разложили Ф, на Р₂ и Ф,.

—Ф, тоже можно разложить. Трос А может пол­
ностью пройти сквозь трос Б, это реальность Р_}. А
вот совпадение оборванных концов — это уже фанта­
стика, то есть Ф,.

—Человечки на одном конце троса должны схва­
тить человечков на другом конце.

—Если представить, что размеры троса Б стре­
мятся к нулю, трос Б свободно пройдет между чело­
вечками троса А...

Шум... С трудом разбираю обрывки фраз: "Маг­ниты... Магнитное сцепление... А если груз тяжелый?.."

Приходится расспрашивать, восстанавливать ход решения. Выясняю, что одни продолжали работать с золотой рыбкой, другие использовали маленьких человечков, третьи — оператор РВС. Приверженцы маленьких человечков вручают мне рисунок: "Тут же все ясно..." Решение у всех одинаковое.

— Правда, похоже на руки? Человечки перехва­тывают руками верхнюю часть троса...

Рис. 6

М. Вертгеймер ОТКРЫТИЕ ГАЛИЛЕЯ*

Как Галилей совершил то открытие, которое привело к формулировке закона инерции и, таким образом, к возникновению современной физики?

Известен целый рад попыток ответить на этот вопрос, однако и до сих пор он остается не вполне ясным. Ситуация, в которой находился Галилей, была отягощена крайне сложными понятиями и спекуля­циями, касавшимися природы движения**.

Предшествующие обсуждения центрировались на такого рода вопросах: направлялось ли мышление Галилея индукцией или абстракцией? Опытным на­блюдением и экспериментом или же некими апри­орными предложениями? Можно ли считать прин­ципиальной заслугой Галилея то, что он превратил качественные наблюдения в количественные? и др.

Если изучить литературу — древние трактаты по физике и работы современников Галилея, — то мож­но обнаружить, что одной из самых замечательных черт мышления Галилея была его способность дос­тигать предельно ясного структурного понимания (insight) на чрезвычайно сложном и запутанном фоне.

Я не буду пытаться дать здесь историческую ре­конструкцию. Это потребовало бы основательного анализа огромного материала первоисточников, а я не историк. К тому же доступный нам исторический материал все равно недостаточен для психолога, интересующегося деталями развивающегося процесса мысли, которые обычно опускаются в тексте. К со­жалению, мы не можем расспросить самого Галилея о действительном ходе его мысли, хотя мне, напри­мер, и очень хотелось бы это сделать, особенно по поводу отдельных моментов. Моя попытка воссоз­дать некоторые линии этого красивого процесса бу­дет в известном смысле лишь психологической ги­потезой, не претендующей на историческую правиль­ность. Но, я думаю, что кое-что мы все-таки смо­жем извлечь из нее для решения нашей проблемы.

Я надеюсь, что читатель будет не только читать, но и попытается думать вместе со мной.

Ситуация следующая:

1) Если взять камень в руку и отпустить его, то
он упадет вниз. Так происходит со всеми тяжелыми
телами. Прежний физик сказал бы: "Тяжелые тела
имеют тяготение к своему дому, земле".

2) Если толкнуть тело, скажем, повозку или мяч
по горизонтальной плоскости, то оно придет в дви-

жение и будет двигаться некоторое время, пока не остановится. Остановка последует скорее, если тол­чок будет слабым, и, наоборот, несколько позже, если толчок будет сильным. Это - самые простые значения старого термина. Рано или поздно движу­щееся тело остановится, если сила, толкавшая его, перестанет действовать. Это очевидно.

3) Имеются некоторые дополнительные факто­ры, которые необходимо рассматривать в связи с анализом движения, а именно: величина объекта, его форма, поверхность, по которой движется тело, наличие или отсутствие препятствий и т. д.

Итак, нам известно огромное число факторов, так или иначе касающихся движения. Вес они хоро­шо нам знакомы. Но понимаем ли мы их? Кажется, что да. На самом деле, разве мы не знаем, чем вызы­вается движение?! Разве мы не можем усмотреть здесь действие некого принципа?

Галилея эти знания не удовлетворяли. Он спро­сил себя: "Знаем ли мы, как действительно проис­ходит такое движение?" Побуждаемый желанием понять внутренние законы движения, Галилей ска­зал себе: "Мы знаем, что тяжелое тело падает, но как оно падает? При падении оно приобретает не­которую скорость. Скорость растет вместе с увеличе­нием пройденного телом пути. Но как именно?"

Обыденный опыт дает нам лишь грубую картину происходящего. Галилей начал наблюдать и экспе­риментировать в надежде обнаружить, что же про­исходит со скоростью и подчиняется ли ее измене­ние каким-либо понятным принципам. Его экспе­рименты представляются чрезвычайно грубыми по сравнению с тем, что достигла физика позже. Но, организуя эти наблюдения и эксперименты, Гали­лей пытался сформулировать свою гипотезу.

Сначала он нашел формулу ускорения падаю­щего тела. Так как скорость падения тела велика и было трудно установить ее точное значение, то Га­лилей решил изучить этот вопрос, рассуждая так: "Не могу ли я исследовать движение более надеж­ным способом? Как я буду изучать, как шарик ска­тывается по наклонной плоскости? Разве свобод­ное падение не есть лишь частный случай движения по наклонной плоскости, когда угол наклона дос­тиг 90"?"

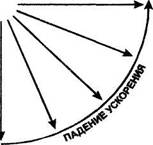
Изучая ускорение в различных случаях, он уви­дел, что оно уменьшается вместе с уменьшением угла наклона (рис. 1). Величине угла соответствует вели­чина уменьшения ускорения.

Ускорение стало самым главным и центральным фактом, как только Галилей усмотрел принципи­альную связь уменьшения ускорения с уменьшени­ем величины угла.

* Хрестоматии по общей психологии. Психология мышления / Под ред. Ю.Б.Гиппеирейтер, В.В.Петухова. М.: Изд-во Моск. ум-га, 1981. С.351— 355.

'* Различались "естественное" и "вынужденное" движения. Существовало понятие производящей силы и спекуляции о роли среды в отсрочке тою момента, когда тело приходит к покою. Существовали определенные представления о "естественных" круговых движениях с постоянной скоростью и т. д.

Потом он вдруг спросил себя: "Не есть ли это лишь половина целой картины?" Не является ли то, что происходит, когда тело подбрасывают вверх или когда шар толкают в гору, другой симметричной ча­стью той же самой картины, частью, которая как отражение в зеркале повторяет то, что есть у нас, и таким образом сообщает картине полноту?

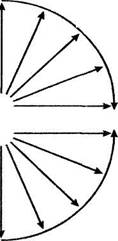
БРОСОК

ПАДЕНИЕ

Рис. 1

Рис. 2

Когда тело подбрасывают вверх, мы имеем не положительное, а отрицательное ускорение. По мере подъема тела его скорость убывает. И опять, симмет­рично положительному ускорению падающего тела, это отрицательное ускорение уменьшается по мере того, как угол наклона все больше отклоняется от 90°, так что получается законченная, полная карти­на (рис. 2).

Но полна ли и эта картина? Нет. В ней есть про­бел. Что будет, когда плоскость горизонтальна, ког­да угол равен нулю, а тело находится в движении? Во всех случаях мы можем начинать с некоторой данной скорости. Что же тогда должно произойти в соответствии с нашей структурой?

Положительное ускорение вниз и отрицательное ускорение вверх уменьшаются при отклонении от вертикали до... и не положительного, и не отрица­тельного ускорения, т. е. ... до постоянного движе­ния?! Если тело движется горизонтально в данном направлении, оно будет продолжать двигаться с по­стоянной скоростью - вечно, если только некая внешняя сила не изменит состояния движения.

Это утверждение находится в крайнем противо­речии с прежним положением, приведенным выше в п. 2. Тело, движущееся с постоянной скоростью, никогда не придет к состоянию покоя, если только не действуют внешние помехи, вне зависимости от того, была ли сила, приведшая тело в движение, сильной или слабой.

Что за странное заключение! Противоречащее на первый взгляд всему обьщенному опыту и все-таки требуемое логикой структуры.

Конечно же, мы не можем выполнить такого эксперимента. Даже если бы мы могли устранить все внешние помехи, чего мы, разумеется, сделать не можем, возможность вечного наблюдения, конеч­на, исключена. С другой стороны, затухание измене­ния ускорения ясно указывает на нулевую величину этого изменения для данного случая.

Точка зрения Галилея подтвердилась и послужила основанием для развития современной физики.

Что существенно для этого описанного здесь процесса?

отрицательного Во-первых, желание выяснить,
ускомшия что же происходит, когда тело падает

,.~™„.~™„ _{или скатывается вниз;} желание по­смотреть, нет ли во всех этих случаях некоего внутреннего принципа; же­лание рассмотреть все случаи при раз­личных углах наклона.

Это центрирует мысль на ускоре­нии. Организация экспериментов оп­ределяется гипотезой о том, что цен-трация на вопросе об ускорении мо­жет привести к пояснению всей про­блемы.

ГМД1НИ1ускорения

Различные случаи выступают как части некой хорошо упорядоченной структуры, указывая на отношение, существующее между углами накло­на и величиной ускорения. Каждый отдельный случай занимает свое ме­сто в группе, и то, что происходит в каждом из этих случаев, может быть понято как оп­ределяемое этим местом.

Во-вторых, эта структура рассматривается теперь как часть более широкого контекста: существует и другая, дополнительная часть, понимаемая как сим­метричная к первой и формирующая целое, в кото­ром эти две половинки представляют собой две боль­ших, соответствующих друг другу подгруппы, с по­ложительным ускорением в одной, с отрицательным — в другой. Они видятся теперь как бы с одной точки зрения, в согласованной структуре целого.

В-третьих, обнаружмаается, что в этой структу­ре существует мекая критическая точка — случай го­ризонтального движения. Структурный принцип це­лого задает ясную необходимость существования именно этой точки. С точки зрения этой необходи­мости случай горизонтального движения выступает как такой случай, при котором не происходит ни ускорения, ни замедления, как случай постоянной скорости. Следовательно, покой становится только частным случаем движения с постоянной скорос­тью, случаем отсутствия положительного или отри­цательного ускорения. Покой и постоянное прямо­линейное движение в горизонтальном направлении выступают теперь как структурные эквиваленты.

Конечно, при этом используются и операции традиционной логики, такие, как индукция, вывод, формулировка теории, равно как и наблюдение, и изобретательное экспериментирование. Но все эти операции функционируют, занимая определенное место внутри целого процесса. Сам же этот процесс управляется той перецентрацией, которая происте­кает из желания добиться осмысленного понимания. Это приводит к трансформации, в результате кото­рой вещи видятся как части новой, ясной структуры. Продуктивные процессы имеют зачастую следу­ющую природу: желание достичь подлинного пони­мания побуждает к исследованию и запускает его. Определенная область в поле исследования выделя­ется как критическая и центральная, но не стано­вится при этом изолированной. Складывается новая, более глубокая, структурная точка зрения на ситуа­цию, вызывая изменения в функциональных значе­ниях отдельных элементов, в их группировке и т. д. Направляясь тем, чего требует структура ситуации

для критической области, приходят к некоторому осмысленному предсказанию, которое, точно так же, как и другие части этой структуры, требует верифи­кации, прямой или косвенной.

Рассказывая эту историю, я часто с чувством глубокого удовлетворения видел, как у многих моих слушателей возникал живой и искренний интерес. Следя за теми драматическими событиями, которые происходили в головах у моих слушателей, я вдруг видел, как в самый критический момент некоторые из них восклицали: "Теперь я понимаю (See)¹.". Для них это был переход от знания некоторого разроз­ненного ряда вещей к углубленному пониманию и осмысленному взгляду на целое.

А.Пуанкаре

МАТЕМАТИЧЕСКОЕ ТВОРЧЕСТВО*

Генезис математического творчества является проблемой, которая должна вызывать живейший интерес у психологов. Кажется, что в этом процессе человеческий ум меньше всего заимствует из внеш­него мира и действует, или только кажется действу­ющим, лишь сам по себе и сам над собой. Поэтому, изучая процесс математической мысли, мы можем надеяться постичь нечто самое существенное в че­ловеческом сознании.

Это было понято уже давно, и несколько меся­цев назад журнал "Математическое образование", издаваемый Лезаном и Фэром, опубликовал вопрос­ник, касающийся умственных привычек и методов работы различных математиков. К тому моменту, когда были опубликованы результаты этого опроса, мой доклад был в основном уже подготовлен, так что я практически не мог ими воспользоваться От­мечу лишь, что большинство ответов подтвердило мои заключения; я не говорю об единогласии, так как при всеобщем опросе на него и нельзя надеяться.

Первый факт, который должен нас удивлять, или, вернее, должен был бы удивлять, если бы к нему не привыкли, следующий: как получается, что существуют люди, не понимающие математики?

Тот факт, что не все способны на открытие, не содержит ничего таинственного. Можно понять и то, что не все могут запомнить доказательство, которое когда-то узнали. Но то обстоятельство, что не вся­кий человек может понять математическое рассуж­дение, когда ему его излагают, кажется совершенно удивительным. И тем не менее людей, которые лишь с большим трудом воспринимают эти рассуждения, большинство; опыт учителя средней школы подтвер­ждает это.

И далее, как возможна ошибка в математике? Нормальный разум не должен совершать логической ошибки, и тем не менее есть очень тонкие умы, ко­торые не ошибутся в коротком рассуждении, подоб­ном тем, с которыми ему приходится сталкиваться в обыденной жизни и которые не способны провес­ти или повторить без ошибки более длинные мате­матические доказательства, хотя в конечном счете последние являются совокупностью маленьких рас­суждений, совершенно аналогичных тем, которые эти люди проводят так легко. Нужно ли прибавить, что и сами хорошие математики не являются непо­грешимыми?

Ответ, как мне кажется, напрашивается сам со­бой. Представим себе длинный ряд силлогизмов, у которых заключения первых служат посылками сле­дующих; мы способны уловить каждый из этих сил­логизмов, и в переходах от посылки к рассуждению мы не рискуем ошибиться. Но иной раз проходит много времени между моментом, когда некоторое

* Хрестоматия по общей психологии. Психология мышления / Под рад. Ю.Е.Гиплвнрейтер, В.В.Пвтухова. М.: Иэд-во Меси, ун­та, 1981. С. 356-365.

предложение мы встречаем в качестве заключения силлогизма, и моментом, когда мы вновь с ним встретимся в качестве посылки другого силлогизма, когда много звеньев в цепи рассуждений, и может случиться, что предложение забыто или, что более серьезно, забыт его смысл. Таким образом, может случиться, что предложение заменяют другим, не­сколько от него отличным, или что его применяют в несколько ином смысле; и это приводит к ошибке.

Если математик должен воспользоваться неко­торым правилом, естественно, он сначала его дока­зывает и в момент, когда это доказательство свежо в его памяти, он прекрасно понимает его смысл и пределы применения и поэтому не рискует его ис­казить. Но затем он применяет его механически, и если память его подведет, то правило может быть применено неверно. В качестве простого и почти вуль­гарного примера можно привести тот факт, что мы часто ошибаемся в вычислении, так как забыли таб­лицу умножения.

С этой точки зрения математические способнос­ти должны были бы сводиться к очень надежной памяти или к безупречному вниманию. Это качество подобно способности игрока в вист запоминать сбро­шенные карты или - на более высоком уровне -способности шахматиста, который должен рассмот­реть большое число комбинаций и все их держать в памяти. Каждый хороший математик должен был бы быть одновременно хорошим шахматистом и обрат­но; точно так же он должен бы быть хорошим вы­числителем. Действительно, так иногда случается, и, например, Гаусс был одновременно гениальным гео­метром и рано проявившим себя очень хорошим вычислителем.

Но есть исключения, хотя, я, пожалуй, не прав, называя это исключениями, так как иначе исклю­чения оказались бы более многочисленными, чем правила. Напротив, это Гаусс был исключением. Что касается меня, то я вынужден признать свою совер­шенную неспособность выполнить сложение без ошибки. Я был бы также очень плохим шахматис­том, я мог бы хорошо рассчитать, что, совершив такой-то ход, я подвергся бы такой-то опасности; я рассмотрел бы много других ходов, которые я от­бросил бы по другим причинам, и кончил бы тем, что совершил бы рассмотренный ход, забыв между делом об опасности, которую я раньше предвидел.

Одним словом, у меня неплохая память, но она недостаточна, чтобы сделать меня хорошим шахма­тистом. Почему же она меня не подводит в трудном математическом рассуждении? Это, очевидно, по­тому, что она руководствуется общей линией рас­суждения. Математическое рассуждение не есть про­стая совокупность силлогизмов: это силлогизмы, помешенные в определенном порядке, и порядок, в котором эти элементы расположены, гораздо более важен, чем сами элементы. Если я чувствую этот по­рядок, так что вижу все рассуждение в целом, то мне не страшно забыть один из элементов: каждый из них встанет на место, которое ему приготовлено, причем без всякого усилия со стороны памяти. Ког­да я изучаю некоторое утверждение, мне кажется, что я сам мог бы его открыть, или, вернее, я пере­открываю его во время изучения.

Отсюда можно сделать вывод, что это интуитив­ное чувство математического порядка, которое по­зволяет нам угадать гармонию и скрытые соотноше­ния, доступно не всем людям. Одни не способны к этому деликатному и трудному для определения чув­ству и не обладают памятью и вниманием сверх обыч­ных: и они совершенно неспособны понимать серь­езную математику; таковых большинство. Другие об­ладают этим чувством в малой степени, но они име­ют хорошую память и способны на глубокое внима­ние. Они запомнят наизусть детали одну за другой, они смогут понять математику и иногда ее приме­нять, но они не способны творить. Наконец, третьи в большей или меньшей степени обладают той спе­циальной интуицией, о которой я говорил, и они могут не только понимать математику, но и творить в ней и пытаться делать открытия, несмотря на то, что их память не представляет собой ничего особен­ного.

Что же такое в действительности изобретение в математике? Оно состоит не в том, чтобы создавать новые комбинации из уже известных математичес­ких фактов. Это мог бы делать любой, но абсолют­ное большинство таких комбинаций не представля­ло бы никакого интереся- Творить - это означает не создавать бесполезных комбинаций, а создавать по­лезные, кошрых ничтожное меньшинство. Творить - это уметь распознавать, уметь выбирать такие фак­ты, которые открывают нам связь между законами, известными уже давно, но ошибочно считавшимися не связанными друг с другом.

Среди выбранных комбинаций наиболее плодо­творными часто оказываются те, которые составле­ны из элементов, взятых из очень далеких друг от друга областей. Я не хочу сказать, что для того, что­бы сделать открытие, достаточно сопоставить как можно более разношерстные факты: большинство комбинаций, образованных таким образом, было бы совершенно бесполезными, но зато некоторые из них, хотя и очень редко, бывают наиболее плодо­творными из всех.

Изобретение — это выбор; впрочем, это слово не совсем точно, — здесь приходит в голову сравне­ние с покупателем, которому предлагают большое количество образцов товаров, и он исследует их один за другим, чтобы сделать свой выбор. В математике образцы столь многочисленны, что всей жизни не хватит, чтобы их исследовать. Выбор происходит не таким образом. Бесплодные комбинации даже не придут и голову изобретателю. В поле зрения его со­знания попадают лишь действительно полезные ком­бинации и некоторые другие, имеющие признаки полезных, которые он аатем отбросит. Все происхо­дит так, как если бы ученый был экзаменатором вто­рого тура, который должен экзаменовать лишь кан­дидатов, успешно прошедших испытания в первом туре.

Настало время продвинуться намного вперед и посмотреть, что же происходит в самой душе мате­матика. Я полагаю, что лучшее, что можно для этого сделать, это провести собственные воспоминания. Я припомню и расскажу вам, как я написал первую свою работу об автоморфных функциях. Я прошу прошения за то, что буду вынужден употреблять спе­циальные термины, но это не должно вас пугать,

так как вам их понимать совсем необязательно. Я, например, скажу, что при таких-то обстоятельствах нашел доказательство такой-то теоремы; эта теоре­ма получит варварское название, которое многие из вас не поймут, но это не важно: для психолога важ­на не теорема, а обстоятельства.

В течение двух недель я пытался доказать, что не может существовать никакой функции, аналогичной той, которую я назвал впоследствии автоморфной. Я был, однако, совершенно не прав; каждый день я садился за рабочий стол, проводил за ним час или два, исследуя большое число комбинаций, и не при­ходил ни к какому результату.

Однажды вечером, вопреки своей привычке, я выпил черного кофе; я не мог заснуть; идеи тес­нились, я чувствовал, как они сталкиваются, пока две из них не соединились, чтобы образовать ус­тойчивую комбинацию. К утру я установил суще­ствование одного класса этих функций, который соответствует гипергеометрическому ряду; мне оставалось лишь записать результаты, что заняло только несколько часов. Я хотел представить эти функции в виде отношения двух рядов, и эта идея была совершенно сознательной и обдуманной; мной руководила аналогия с эллиптическими функ­циями. Я спрашивал себя, какими свойствами должны обладать эти ряды, если они существуют, и мне без труда удалось построить эти ряды, ко­торые я назвал тета-автоморфными.

В этот момент я покинул Кап, где я тогда жил, чтобы принять участие в геологической экскурсии. Перипетии этого путешествия заставили меня забыть о моей работе. Прибыв в Кутанс, мы сели в омни­бус, для какой-то прогулки; в момент, когда я встал на подножку, мне пришла в голову идея, без вся­ких, казалось бы, предшествовавших раздумий с моей стороны, идея о том, что преобразования, ко­торые я использовал, чтобы определить автоморф-ные функции, были тождественны преобразовани­ям неевклидовой геометрии. Из-за отсутствия вре­мени я не сделал проверки, так как, с трудом сев в омнибус, я тотчас же продолжил начатый разговор, но я уже имел полную уверенность в правильности сделанного открытия. По возвращении в Кан я на свежую голову проверил найденный результат.

В то время я занялся изучением некоторых воп­росов теории чисел, не получая при этом никаких существенных результатов и не подозревая, что это может иметь малейшее отношение к прежним ис­следованиям. Разочарованный своими неудачами, я поехал провести несколько дней на берегу моря и думал совсем о другой вещи. Однажды, когда я про­гуливался по берегу, мне также внезапно, быстро и с той же мгновенной уверенностью пришла на ум мысль, что арифметические преобразования квад­ратичных форм тождественны преобразованиям не­евклидовой геометрии.

Возвратившись в Кан, я думал над этим резуль­татом, извлекая из него следствия; пример квадра­тичных форм мне показал, что существуют автоморф-ные группы, отличные от тех, которые соответству­ют гипергеометрическому ряду; я увидел, что могу к ним применить теорию тета-автоморфных функций и что, следовательно, существуют автоморфные функ­ции, отличающиеся от тех, которые соответствуют

гипергеометрическому ряду, — единственные, кото­рые я знал до тех пор.

Естественно, я захотел построить все эти функ­ции; я предпринял систематическую осаду и успеш­но брал одно за другим передовые укрепления. Оста­валось, однако, еше одно, которое держалось и взя­тие которого означало бы падение всей крепости. Однако сперва ценой всех моих усилий я добился лишь того, что лучше понял, в чем состоит труд­ность проблемы, и это уже кое-что значило. Вся эта работа была совершенно сознательной.

Затем я переехал в Мон-Валерьян, где я должен был продолжать военную службу. Таким образом, занятия у меня были весьма разнообразны. Однаж­ды, во время прогулки по бульвару, мне вдруг при­шло в голову решение этого трудного вопроса, ко­торый меня останавливал. Я не стал пытаться вни­кать в него немедленно и лишь после окончания службы вновь взялся за проблему. У меня были все элементы и мне оставалось лишь собрать их и приве­сти в порядок. Поэтому я сразу и без всякого труда полностью написал эту работу.

Я ограничусь лишь этим одним примером. Бес­полезно их умножать, так как относительно других моих исследований я мог бы рассказать вещи, со­вершенно аналогичные.

То, что вас удивит прежде всего, это видимость внутреннего озарения, являющаяся результатом дли­тельной неосознанной работы; роль этой бессозна­тельной работы в математическом изобретении мне кажется несомненной. Часто, когда работают над трудным вопросом, с первого раза не удается ниче­го хорошего, затем наступает более или менее дли­тельный период отдыха и потом снова принимаются за дело. В течение первого получаса дело вновь не двигается, а затем вдруг нужная идея приходит в го­лову. Можно было бы сказать, что сознательная ра­бота стала более плодотворной, так как была пре­рвана и отдых вернул уму силу и свежесть. Но более вероятно предположить, что этот отдых был запол­нен бессознательной работой и что результат этой работы внезапно явился математику точно так, как это было в случае, который я рассказывал; только озарение вместо того, чтобы произойти во время прогулки или путешествия, происходит во время сознательной работы, но совершенно независимо от этой работы, которая, самое большее, играет роль связующего механизма, переводя результаты, полу­ченные во время отдыха, но оставшиеся неосознан­ными, в осознанную форму.

Есть еще одно замечание по поводу условий этой бессознательной работы: она возможна или, по край­ней мере, плодотворна лишь в том случае, когда ей предшествует и за ней следует сознательная работа. Приведенный мной пример подтверждает, что эти внезапные вдохновения происходят лишь после не­скольких дней сознательных усилий, которые каза­лись абсолютно бесплодными, и когда кажется, что выбран совершенно ошибочный путь. Эти усилия, однако, пустили в ход бессознательную машину, без них она не пришла бы в действие и ничего бы не произвела.

Необходимость второго периода сознательной работы после озарения еше более понятна. Нужно использовать результаты этого озарения, вывести из

них непосредственные следствия, привести в поря­док доказательство. Но особенно необходимо их про­верить. Я вам уже говорил о чувстве абсолютной уве­ренности, которое сопровождает озарение; в расска­занных случаях оно не было ошибочным, но следует опасаться уверенности, что это правило без исклю­чения; часто это чувство нас обманывает, не стано­вясь при этом менее ярким, и заметить это можно лишь при попытке строго сознательно провести до­казательство. Особенно я наблюдал такие факты в случае, когда идеи приходят в голову утром или ве­чером в постели, в полусознательном состоянии.

Таковы факты. Рассмотрим теперь выводы, ко­торые отсюда следуют. Как вытекает из предыдуще­го, или мое "бессознательное я", или, как это назы­вают, мое подсознание, играет основную роль в ма­тематическом творчестве. Но обычно рассматривают подсознательные процессы как явления, протекаю­щие чисто автоматически. Мы видим, что работа математика не является просто механической и ее нельзя было бы доверить машине, сколь бы совер­шенной ока ни была. Здесь дело не только в том, чтобы создавать как можно больше комбинаций по некоторым известным законам. Истинная работа уче­ного состоит в выборе этих комбинаций, так чтобы исключить бесполезные или, вернее, даже не утруж­дать себя их созданием. И правила, которыми нужно руководствоваться при этом выборе, предельно де­ликатны и тонки, их почти невозможно выразить точными словами; они легче чувствуются, чем фор­мулируются; как можно при таких условиях пред­ставить себе аппарат, который их применяет авто­матически?

Отсюда перед нами возникает первый вопрос: "Я — подсознательное" нисколько не является низ­шим по отношению к "Я - сознательному", оно не является чисто автоматическим, оно способно здраво судить, оно умеет выбирать и догадываться. Да что говорить, оно умеет догадываться лучше, чем мое сознание, так как преуспевает там, где сознание это­го не может.

Короче, не стоят ли мои бессознательные про­цессы выше, чем мое сознание? Не вытекает ли ут­вердительный ответ из фактов, которые я только что вам изложил? Я утверждаю, что не могу с этим со­гласиться. Исследуем еще раз факты и посмотрим, не содержат ли они другого объяснения.

Несомненно, что комбинации, приходящие на ум в виде внезапного озарения после длительной бессознательной работы, обычно полезны и глубо­ки. Значит ли это, что подсознание образовало толь­ко эти комбинации, интуитивно догадываясь, что лишь они полезны, или оно образовало и многие другие, которые были лишены интереса и остались неосознанными?

При этой второй точке зрения все эти комбина­ции формируются механизмом подсознания, но в поле зрения сознания попадают лишь представляю­щие интерес. Но и это еще очень непонятно. Каковы причины того, что среди тысяч результатов деятель­ности нашего подсознания есть лишь некоторые, которые призваны пересечь его порог? Не просто ли случай дает нам эту привилегию? Конечно, нет. К примеру, среди всех ощущений, действующих на наши органы чувств, только самые интенсивные

обращают на себя наше внимание, по крайней мере, если это внимание не обращено на них по другим причинам В более общем случае среди бессознатель­ных идей привилегированными, т. е. способными стать сознательными, являются те, которые наиболее глу­боко воздействуют на наши чувства.

Может вызвать удивление обращение к чувствам, когда речь идет о математических доказательствах, которые, казалось бь», связаны только с умом. Но это означало бы, что мы забываем о чувстве матема­тической красоты, чувстве гармонии чисел и форм, геометрической выразительности. Это настоящее эс­тетическое чувство, знакомое всем настоящим ма­тематикам. Воистину, здесь налицо чувство!

Но каковы математические характеристики, ко­торым мы приписываем свойства красоты и изяще­ства и которые способны возбудить в нас своего рода эстетическое чувство? Это те элементы, которые гар­монически расположены таким образом, что ум без усилия может их охватить целиком, угадывая детали. Эта гармония служит одновременно удовлетворени­ем наших эстетических чувств и помощью для ума, она его поддерживает, и ею он руководствуется. Эта гармония дает нам возможность предчувствовать ма­тематический закон. Единственными фактами, спо­собными обратить на себя наше внимание и быть полезными, являются те, которые подводят нас к познанию математического закона. Таким образом, мы приходим к следующему выводу: полезные ком­бинации - это те, которые больше всего воздейству­ют на это специальное чувство математической кра­соты, известное всем математикам и недоступное профанам до такой степени, что они часто склонны смеяться над ними.

Что же, таким образом, происходит? Среди мно­гочисленных комбинаций, образованных нашим под­сознанием, большинство безынтересно и бесполез­но, но потому они и не способны подействовать на наше эстетическое чувство; они никогда не будут нами осознаны; только некоторые являются гармо­ничными и потому одновременно красивыми и по­лезными; они способны возбудить нашу специаль­ную геометрическую интуицию, которая привлечет к ним наше внимание и таким образом даст им воз­можность стать осознанными.

Это только гипотеза, но есть наблюдение, кото­рое ее подтверждает: внезапное озарение, происхо­дящее в уме математика, почти никогда его не об­манывает. Иногда случается, что оно не выдержива­ет проверки, и тем не менее почти всегда замечают, что если бы эта ложная идеи оказалась верной, то она удовлетворила бы наше естественное чувство ма­тематического изящества.

Таким образом, это специальное эстетическое чувство играет роль решета, и этим объясняется, почему тот, кто лишен его, никогда не станет на­стоящим изобретателем.

Однако преодолены не все трудности; ясно, что пределы сознания очень узки, а что касается под­сознания, то его пределов мы не знаем. Эти пределы тем не менее существуют, но правдоподобно пред­положить, что подсознание могло бы образовать все возможные комбинации, число которых испугало бы воображение, и это кажется и необходимым, так как если бы оно образовало их мало и делало бы это

случайным образом, то маловероятно, чтобы "хоро­шая" комбинация, которую надо выбрать, находи­лась среди них.

Для объяснения надо учесть первоначальный период сознательной работы, который предшеству­ет плодотворной бессознательной работе. Прошу из­винить меня за следующее грубое сравнение. Пред­ставим себе будущие элементы наших комбинаций как что-то похожее на атомы — крючочки Эпикура. За время полного отдыха мозга эти атомы непод­вижны, они как будто прикреплены к стене; атомы при этом не встречаются и, следовательно, никакое их сочетание не может осуществиться. Во время же кажущегося отдыха и бессознательной работы неко­торые из них оказываются отделенными от стены и приведенными в движение. Они перемешаются во всех направлениях пространства, вернее, помеще­ния, где они заперты, так же как туча мошек или, если вы предпочитаете более ученое сравнение, как газовые молекулы в кинетической теории газов. При взаимном столкновении могут появиться новые ком­бинации.

Какова же роль первоначальной сознательной работы? Она состоит, очевидно, в том, чтобы мо­билизовать некоторые атомы, отделить их от стены и привести в движение. Считают, что не сделано не­чего хорошего, так как эти элементы передвигали тысячами разных способов с целью найти возмож­ность их сочетать, а удовлетворительной комбина­ции найти не удалось. Но после того импульса, ко­торый им был сообщен по нашей воле, атомы боль­ше не возвращаются в свое первоначальное непод­вижное состояние. Они свобо<