Концентрация какого компонента в ОГ самая высокая?

Показатели:

> углеводороды;

> оксид углерода СО;

> альдегиды СНО;

> бенз(а)пирен;

> соединения свинца;

> сажа.

Контрольные вопросы

1. Что такое ранговый анализ?

2. Зачем выполняется ранжирование?

3. Каковы правила присвоения рангов признакам?

4. Как определяется показатель равных рангов?

5. Как по сумме рангов следует расположить признаки в ряду важно­сти?

6. Какой признак считается самым важным?

7. Что такое "степень согласованности"?

8. Как определяется "коэффициент конкордации"?

9. Какие заключения и как можно сделать о степени согласованности?

Практическое занятие № 3

Исследование статического давления автомобильного колеса на опорную плоскость

Цель занятия - на конкретном примере показать различные элементы

научных исследований (НИ) и использование методов

теоре­тических исследований.

Содержание занятие

1.По литературе [1, с. 24-29; 53-70; 2, с. 79-87; 3, с. 20-24, 33-38] вос­становить в памяти или расширить знания об этапах и методах теоретиче­ских исследований самостоятельно при домашней подготовке.

2. Внимательно разобраться в приведённой ниже методике исследова­ния

3. Вписать в отчёт основные этапы исследования и использованные ма­тематические выражения. При этом показать, где и какой метод использо­ван.

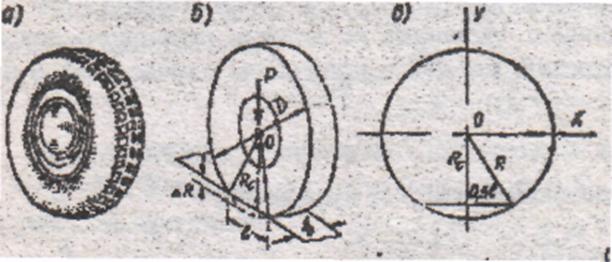
4. Зарисовать абстрактный объект исследований (рис. 2"б" и "в").

5. Выполнить проверку правильности выражения (10) по размерности и сравнением расчётных значений " 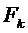" и "р" с экспериментальными (по ин­дивидуальному заданию).

6. Проанализировать по выражению (10), как зависит удельное давление от каждого из факторов и отразить результаты анализа в отчёте.

7. Уточнить зави­симость удельного давления от P_z и С_ш:

а) способом дифференцирования в частных производных (получить са­мостоятельно частные производные и сравнить их с приведёнными в МУ);

б) графическим методом построить графики р = f (P_z , 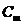) по индиви­дуальному заданию, выданному преподавателем.

8. Оформить отчёт.

Отчёт должен содержать результаты выполнения по пунктам 3 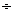7 содержания занятия с соответствующими таблицами и графиками, заклю­чение. В заключении указываются результаты анализа по пунктам 6 и 7.

Рисунок 2 - : а - автомобильное колесо; б - упру­гий диск; в – окружность

Методическая информация

Этапы НИ и методы, применённые в примере

Постановка задачи.

Наложение ограничений.

Выдвижение гипотезы.

Развитие гипотезы. При этом используются:

♦ метод аналогии;

♦ метод абстрагирования;

♦ упрощения и допущения.

Развитие теории:

♦ элементарная проверка (проверка формулы по размерности);

♦ экспериментальная проверка.

Теоретическое исследование.

♦ аналитическое;

♦ графическое. Выводы.

Постановка задачи

Для выбора покрытия площадки хранения автомобилей необходи­мо исследовать статистическое удельное давление автомобильного колеса на опорную поверхность покрытия.

Ограничение — удельное давление не должно превышать несущей способности состава покрытия, так как в противном случае колесо будет его продавливать.

Методика выполнения

Известно следующее математическое выражение :

,

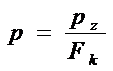где 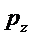- нагрузка на колесо, кН;

р - удельное давление, кПа;

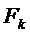- площадь контакта колеса, м².

Выдвижение гипотезы: удельное давление зависит от нагрузки Р_г и диаметра колеса D, так как 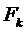зависит от размеров колеса и шины, пока не­известным нам образом.

Развитие гипотезы: наблюдая за автомобилем и упругими качества­ми автошины, замечаем аналогию с законом Гука (метод аналогии)

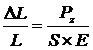, (1)

где L и 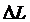- длина стержня и величина его абсолютного сжатия, м;

Р - нагрузка, кН;

S - площадь поперечного сечения, м²; Е -модуль упругости материала, кПа.

Абстрагирование. Вообразим автомобильное колесо с эластичной шиной (рис. 2а) в виде эластичного упругого цилиндрического барабана (рис. 26) диаметром D и высотой b, равной ширине автошины.

Развитие теории. В результате приложения нагрузки Р_z барабан деформируется на величину AR и его статический радиус равен

R = 0,5D- 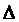R. (2)

Площадь контакта колеса с дорогой

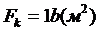, (3)

где 1 - длина площади контакта колеса с дорогой, м;

b - ширина площади контакта колеса с дорогой, м.

Учитывая рисунок протектора, вводим коэффициент полноты кон­такта, равный 0,8.

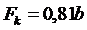. (4)

Основные упрощения, допущенные при абстрагировании: цилинд­рическая форма колеса и однородность материала, -требуют доказатель­ства в эксперименте.

Возвращаясь к аналогии и учитывая следующие соответствия:

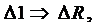
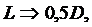
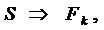
из выражения закона Гука

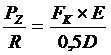. (5)

Обозначив правую часть через Сщ, получаем формулу для коэффи­циента жесткости шины:

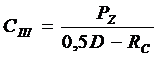. (6)

Длину площади контакта 1 определяем из уравнения окружности

(х² + у²) =R², Учитывая соответствия: 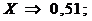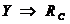и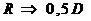

(см. рис. 2в), получаем

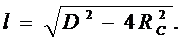
Из выражения (6) находим R_c.

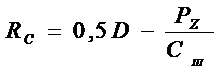. (8)

Подставляя (8) в (7) и затем полученное выражение в (4), имеем

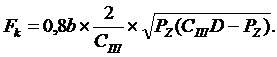
И, наконец, окончательное выражение для удельного давления

.

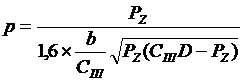Элементарная проверка правильности формулы по размерности зна­менателя

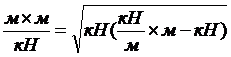. (10)

Учитывая принятые нами. упрощения, полученная формула приближенная и нуждается в экспериментальной проверке ее погрешно­сти.

Для этого:

1) рассчитаем удельное давление "р" для двух автошин 6.00-16 и 260-20 (см. табл. 3);

2) сравниваем рассчитанные значения с экспериментальными данными (табл. 4).

Таблица 3 - Расчёт удельного давления колеса

Обозначе­ние шины	Диаметр шины без нагрузки D, м	Ширина профиля без нагруз­ки Ь, м	Коэффици­ент жестко­сти Сш, кН/м	Нагрузка на шину Р2, кН	Удельное давление р, кПа
6.00-16	0,725	0,162	480,3	4,4	210,8
260-20	1,038	0,275	1216,0	10,4	252,0

Таблица 4 - Сравнительный анализ фактических и расчётных данных

Обозначе­ние шины	Площадь контакта F,, м2	Удельное давление р, кПа
факти­ческая	рас­чётная	% расхо­ждения	факти­ческое	расчет­ное	% расхо­ждения
6.00-16	0,0195	0,0207	+6,2	225,6	210,8	-6,5
260-20	0,0385	0,0413	+7,3	264,8	252,0	-4,8

Полученная формула для "р" не дает оснований считать теорети­ческое исследование завер­шенным, так как влияние раз­меров автошины "Ь" и "D" -очевидно, но о влиянии нагруз­ки "Р_z" на автошину и её жёст­кости "С_ш^м можно судить лишь с некоторой вероятностью пред­положения.

Для выявления этого влияния предлагаются два спо­соба:

-дифференцирование функции р = f (P_z, 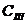,) в частных производных при D = const и b = const для конкретной автошины и определение знака произ­водной;

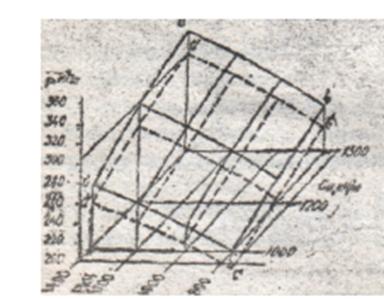
- графический, т.е. построение в трёхмерной системе координат графи­ка функции р = f(P_z, ).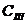

Индивидуальные задания для самостоятельной работы выдаются преподавателем каждому студенту в следующем виде:

a) параметры автошины, по которым студент рассчитывает "F_K" и "р" н сравнивает их с экспериментальными значениями. Результаты расчёта представляются студентом по форме табл. 3, а сравнение по форме табл. 4;

b) ряд значений "P_z" и "С_ш "> по которым студент строит график р = f (P_z, Сш) для своей автошины. Пример задания показан в табл. 5.

Таблица 5 - Расчётные значения P_z и.Сщ

Автошина	Р2,кН	СькН/м
6.00-16		3,5		4,5
260-20	. 5

Находим частные производные

/

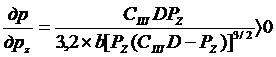
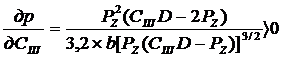Обе частные производные положительны, так как разност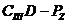и > 0 и 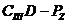> 0 при всех практически возможных значениях P_z, 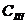и 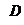. Поэтому увеличение значений P_z и Сш приводит к увеличению удельно­го давления р.

Контрольные вопросы

1. Перечислите основные этапы НИ.

2. Перечислите основные методы развития гипотезы и теории.

3. Расскажите о методах аналогии.

4. Расскажите о вещественном моделировании.

5. Расскажите о воображаемом моделировании.

6. Абстрагирование и его разновидности.

7. Применение «упрощений» и «допущений» в НИ.

8. Понятие об аналитическом теоретическом исследовании.

9. Понятие о графическом теоретическом исследовании.

10. Как выполняется экспериментальная проверка формулы по размер­ности?

11. Причины приближённости результатов, полученных при теоретиче­ских исследованиях.

12. Как оценить степень погрешности результатов, полученных при теоретических исследованиях?

13. Как определяется влияние аргумента на функцию методами диффе­ренцирования и графическим?

Практическое занятие N 4

Постановка задания НИ и составление матрицы математического

Планирования

Цель занятия - на конкретном примере исследования влияния поло­жения дроссельной Заслонки и угла опережения зажигания на мощность автомобильного двигателя ЗИЛ-130 научиться составлять матрицу матема­тического планирования.

Содержание занятия

1. По литературе [1, с. 145-150 ; 4, с. 97-118 ; 5, с. 64 -72] восстановить в памяти и углубить знания о математическом планировании эксперимента (самостоятельно при домашней подготовке).

2. По настоящим МУ ознакомиться с постановкой задачи и методикой выполнения планирования эксперимента.

3. По индивидуальному заданию, выданному преподавателем, выпол­нить шаги 1-4 (см. методическую информацию).

4. Построить матрицу проведения эксперимента в соответствии с табл. 6а для своего варианта задания, выполняя шаги 5 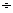7 .

(см. методическую информацию).

5. Оформить отчёт.

Отчет должен содержать краткое описание расстановки задачи и ос­новных шагов математического планирования эксперимента; расчётные формулы, рисунок "черного ящика", матрицу' эксперимента (табл. 6а и 66), заключение. В заключении указываются результаты постановки задачи: факторы, параметры, ограничения, необходимое число опытов для полно-факторного и частичного плана эксперимента. Табл. 6 оформляется только один раз (см. п. 4 задания), а затем заполняется по мере выполнения зада­ний П3№3и4.

Методическая информации

Постановка задачи

В теории автомобильных двигателей известна зависимость мощно­сти двигателя N_e от частоты вращения коленчатого вала (Nдв,) и вращаю­щего момента на выходе двигателя (Мвр). Однако эти факторы сами явля­ются зависимыми от положения дроссельной заслонки (Др), угла опереже­ния зажигания ( 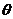₃). Последние зависимости теоретически не установлены. Нам необходимо найти такое математическое выражение, которое позво­лило бы найти оптимальное сочетание Др и 6₃ с точки зрения достижения максимальной мощности N_e двигателя (ЗИЛ-130) для конкретных значений частоты вращения коленчатого вала п_т =1500 мин"¹, т.е. найти функцию отклика N_e = f (Др, 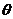₃) при n_да= const.

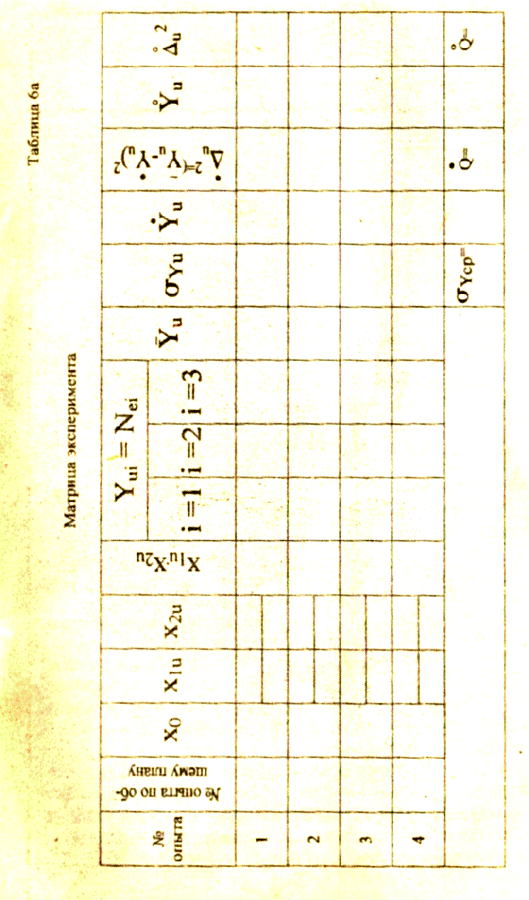
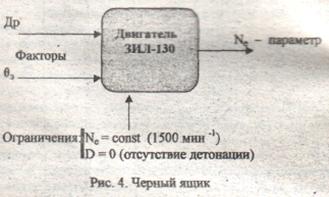
Поскольку теоретически определить ее не представляется возмож­ным, то мы имеем дело с "черным ящиком" (см. рис. 4). Под "чёрным ящи­ком" понимается объект, внутреннее содержание которого и происходящие в нём процессы нам неизвестны.

С целью аппроксимации функция отклика полагаем, что существует уравнение регрессии: N_e = f (Др, 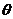₃), адекватно описывающее процессы сгорания в цилиндре двигателя, т. е. формирующий линейный поли­ном. Математически это уравнение можно представить в виде линейного двучлена Y = 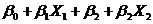₃. Задача состоит в определении коэффициен­тов уравнения регрессии .

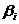Методика выполнения

Из постановки задачи устанавливаем, что цель исследования -оптимизация факторов Др и 0₃ для параметра N_e, иначе говоря, имеем функцию цели Y = f (X) Д₂), где Y = N_e X) = Др Х1 = 0₃. Для определения коэффициентов используем полнофакторный эксперимент (ПФЭ), метод наименьших квадратов (МНК) и осуществляем следующие шаги.

1. Для определения факторного пространства выполняем предва­рительные эксперименты с наложением указанных на рис. 4 ограничений:

В результате получаем области определения факторов: для положения дроссельной заслонки Др- от 25 до 50 %; для угла опережения зажигания 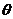₃ - от -20 до -30 °ПКВ (градусов поворота коленчатого вала). Здесь интер­вал для Др определен из условия п_дв= 1500, а для 6, из условия отсутствия детонации двигателя, обозначенного как D = 0.

2. Определяем уровни варьирования факторов. Для первого фактора Др принимаем уровни Дрmin ⁼ 25% и Дрmin ⁼ 50%; тогда интервал варьи­рования 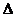Др = (50 -25)/2 = 12,5%. Условие 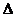Др 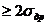заведомо выполня­ется, так как точность установки положения дроссельной заслонки Др со­ставляет 1%. Основной уровень для неё Др_о= (25+50)/2 = =37,5%.

Для второго фактора 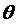₃, принимаем уровни 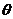_3min ⁼25 °ПКВ и 30°ПКВ до ВМТ. Для точного задания 0₃ отключаем автоматы зажигания и заменяем их диском с градуированной шкалой и ценой деления 1°ШСВ.

Для определения 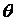₃, проводим дополнительные эксперименты и по­лучаем следующие значения 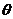_3j -: 31; 30,5; 28,5; 30; 29,5 °ПКВ при установ­ленном по диску значении 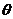₃ = 30 °ПКВ и определяем среднеквадратическое отклонение

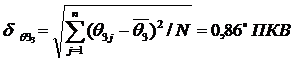_3.

Тогда интервал варьирования А 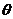₃= (30 - 25)12 = 2,5 °ПКВ больше, чем 2 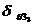⁼ 1,72 °ПКВ. Таким образом, необходимое соотношение между вели­чиной интервала варьирования и точностью установки обоих факторов со­блюдается. Основной уровень 0,0= (25+30)/2 = 27,5°ПКВ.

3. Кодируем уровни факторов

xi = (Дрi –Др0)/Др = ± 1; х₂ = ( 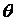_3i - 0_ЗО)/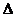 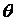₃ = ± 1.

После кодирования предполагаемое уравнение регрессии (аппрок­симирующий линейный полином) представляется в виде:

.

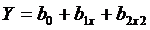4. Определяем количество опытов. Так как имеем два фактора с дву­мя уровнями, то при полнофакторном эксперименте достаточно выполнить N = Т - 2²=4 опыта, где к - количество факторов.

5. Составляем матрицу эксперимента N = 2² (табл. 66).

План эксперимента задается графами (столбцами) 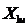и . . Первая . строка матрицы соответствует первому опыту, выполненному при сочета­нии нижних уровней обоих факторов (координаты -1,-1). Для простоты в матрице проставляются только знаки координат «+» или «-». Для второго опыта переходим с нижнего уровня фактора xi на верхний, сохраняя ниж­ний уровень фактора х1. В третьем и четвёртом опытах переходим с ниж­него уровня х1 на верхний. Уровни фактора xl повторяются как в опытах 1 и 2 соответственно. Таким образом, получаем все четыре возможных соче­тания уровней факторов.

6. Для учёта нелинейного аппроксимирующего полинома, который может иметь место при эффекте взаимодействия факторов, следует в урав­нении регрессии добавить член с произведением х_1* х₂. Тогда,

.

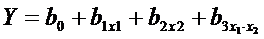Эффект взаимодействия означает, что влияние одного фактора на Y зависит от того, какое значение принимают другие факторы. При этом в матрице добавляется столбец х_1* х₂.Для реального осуществления опытов, вы необходимо знать сочетание фактических (а не кодированных) уровне факторов. Для этого строки в столбцах Х) и х₂ делим на две подстроки.

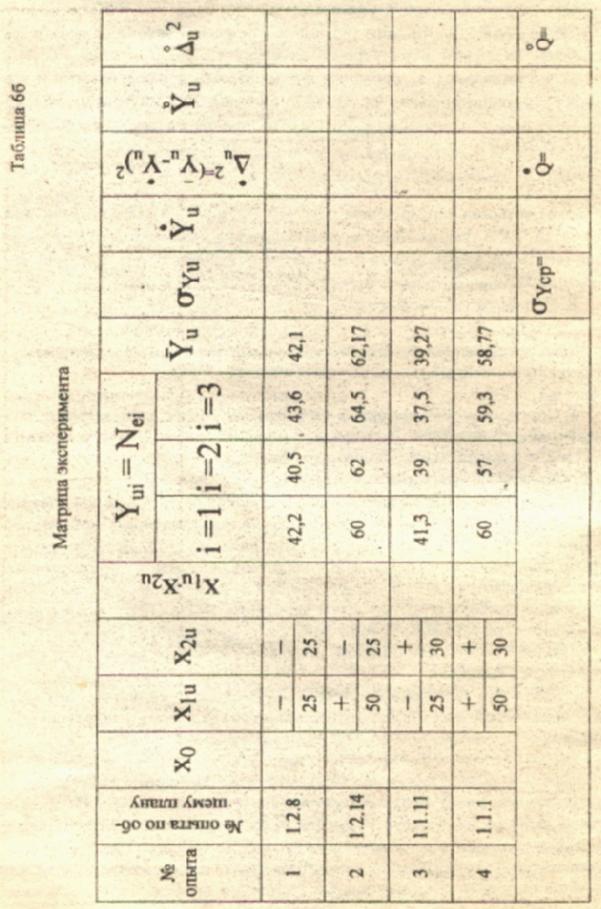
В трапе я подстроке проставлены кодированные уровни, а в нижней - соответствующие им фактические. Учитывая то обстоятельство, что уровни факторов лежат в малой области пространства, определяемой близостью к п_да = 1500 мин "', наша матрица является только частью общей матрицы, охватывающей всё общее факторное пространство. Вводим дополнитель­ный столбец «№ опыта по плану», отражающий нумерацию наших опытов в матрице общего плана эксперимента.

7. Выполняем опыты (в ПЗ условно) и результаты опытов Y_u заносим в матрицу (в ПЗ значения результатов опытов по п. 4 задания даёт препо­даватель). Для уменьшения погрешности эксперимента каждый опыт по­вторяем 1 раз (i = 1,2,3) и вычисляем для каждого опыта (и =1,2,3,4, где и - номер опыта) средние арифметические значения параметра Y_u.

Контрольные вопросы

1. Объяснить смысл понятия "математического планирования экспери­мента".

2. Суть классического плана эксперимента.

3. Понятие рандомизированного плана эксперимента.

4. Понятие сбалансированного плана эксперимента.

5. Объяснить понятия; фактор, параметр, отклик, функция цели, - ис­пользуемые в планировании эксперимента.

6. Что означает понятие "уравнение регрессии".

7. Что означает понятие "поверхность отклика".

8. Охарактеризовать требования к выбору фактора.

9. Объяснить понятия: факторное пространство, область.

10. Что такое интервал варьирования фактора.

11. Как выбираются уровни фактора.

12. Что означает понятие "плановый эксперимент".

13. Что означает понятие "реплика плана эксперимента".

14. Что такое "чёрный ящик".

15. Объяснить разницу между фактическим и кодированным значения­ми факторов.

16. Что такое основной уровень фактора.

17. Как выполняется кодирование уровней факторов.

18. Как составляется основная часть плана (матрицы) эксперимента.

19. Объяснить понятие "эффект взаимодействия факторов".

20. Как учитывается нелинейность типа эффект взаимодействия факторов при планировании эксперимента.

Практическое занятие №5