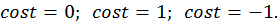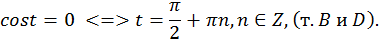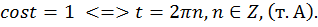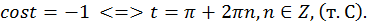Применение некоторых стратегий развития критического мышления на практике изучения тригонометрических функций

2.1 Знакомство с понятием “Три­го­но­мет­ри­че­ские урав­не­ния” с применением стратегии ЗХУ

Здесь лучше всего использовать прием “Знаю - хочу узнать – узнал”.Ученики могут использоватьсвои предыдущий опыт в знании тригонометрии. Каждая функция рассматривалась в 9-ом классе. Нарисовав таблицу они могут опереться на столбец “Знаю”.Таким образом им будет легче запоминать новый материал.

1. Тема урока, введение:

Мы рас­смот­рим и решим про­стей­шие три­го­но­мет­ри­че­ские урав­не­ния вида

.

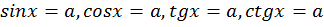Ответьте на вопрос: Что означают эти записи?

В процессе обсуждения в группах школьники заполняют первые два столбца таблицы:

Знаю	Хочу знать	Узнал

Целью применения стратегии является выявление понимания школьниками понятия уравнения, значения каждого из элементов записи: что дано, что нужно найти. А также ожидается, что им удастся поставить новую учебную задачу, заполнив вторую графу таблицы. Таким образом, должна быть достигнута осмысленность дальнейшей учебной деятельности по усвоению методов решения указанных видов уравнений. По завершении работы школьников по разбору нового материала, они заполняют третью графу таблицы. Эту часть работы целесообразно выполнить индивидуально. В этом случае учителю будет предоставлен материал для мониторинга процесса овладения темой урока каждым учеником.

2. Решение уравнения вида sinx=a:

При­мер 1. Ре­шить урав­не­ние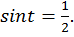

Ре­ше­ние:

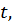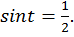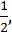Ре­шить урав­не­ние – это найти мно­же­ство всех зна­че­ний при каж­дом из ко­то­рых Это урав­не­ние имеет ре­ше­ние, т.к. число вхо­дит в мно­же­ство зна­че­ний си­ну­са. На линии си­ну­сов от­ме­тим про­ве­дем пер­пен­ди­ку­ляр до пе­ре­се­че­ния с окруж­но­стью и по­лу­чим точки 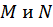(рис. 1). Толь­ко эти две точки имеют ор­ди­на­ту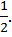

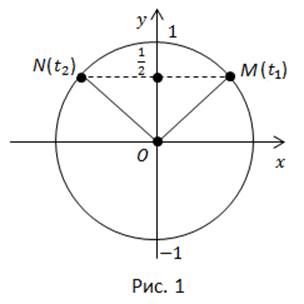
По­лу­чен­ным точ­кам со­от­вет­ству­ют мно­же­ства дей­стви­тель­ных чисел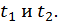

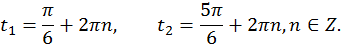
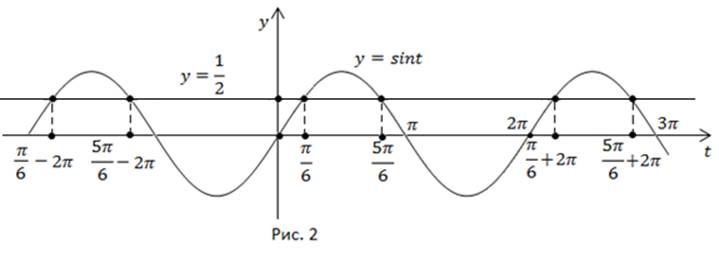
Про­ил­лю­стри­ру­ем ре­ше­ние того же урав­не­ния на гра­фи­ке.

Для того, чтобы ре­шить урав­не­ние 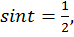необ­хо­ди­мо по­стро­ить гра­фи­ки функ­ций 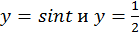и найти абс­цис­сы точек их пе­ре­се­че­ния (рис. 2).

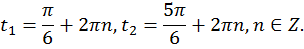
Ответ: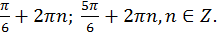

3. Решение уравнения вида cosx=a:

При­мер 2. Ре­шить урав­не­ние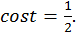

Ре­ше­ние:

Число 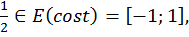зна­чит, урав­не­ние имеет ре­ше­ния.

Тре­бу­ет­ся найти мно­же­ство всех 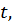при каж­дом из ко­то­рых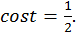

От­ме­тим на линии ко­си­ну­сов точку 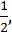про­ве­дем пер­пен­ди­ку­ляр до пе­ре­се­че­ния с окруж­но­стью и по­лу­чим две точки – (рис. 3).

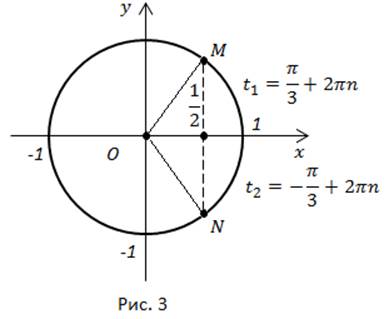
По­лу­чен­ным точ­кам со­от­вет­ству­ют мно­же­ства дей­стви­тель­ных чисел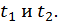

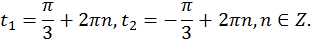
Ответ: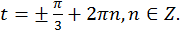

Про­ил­лю­стри­ру­ем ре­ше­ние на гра­фи­ке функ­ции (рис. 4).

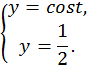
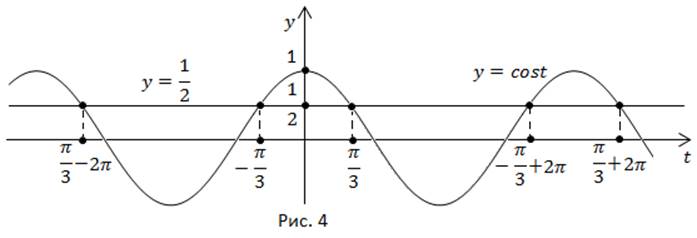
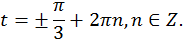
Ответ: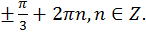

4. Решение уравнения вида tgx=a:

При­мер 3. Ре­шить урав­не­ние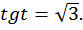

Ре­ше­ние:

На линии тан­ген­сов от­ло­жим 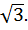Со­еди­ним эту точку с цен­тром чис­ло­вой окруж­но­сти и по­лу­чим две точки пе­ре­се­че­ния с окруж­но­стью – 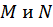(рис. 5).

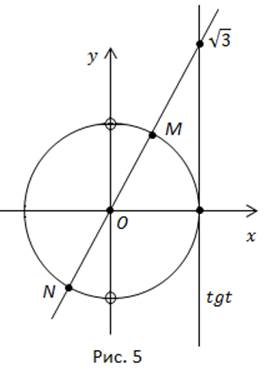
Точке M со­от­вет­ству­ет мно­же­ство чисел 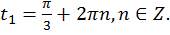Точке 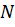со­от­вет­ству­ет мно­же­ство чисел 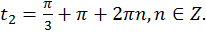Эти два мно­же­ства чисел можно за­пи­сать в виде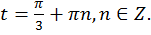

Про­ил­лю­стри­ру­ем ре­ше­ние на гра­фи­ке (рис. 6).

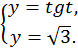
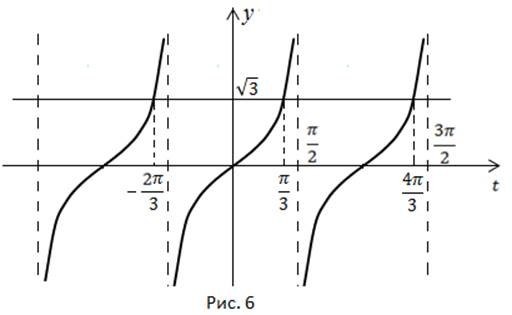
Ответ: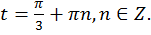

5. Решение уравнения вида ctgx=a:

При­мер 4. Ре­шить урав­не­ние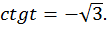

Ре­ше­ние:

От­ме­тим на линии ко­тан­ген­сов точку 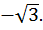Со­еди­ним её с на­ча­лом ко­ор­ди­нат и по­лу­чим на окруж­но­сти две точки – 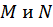(рис. 7).

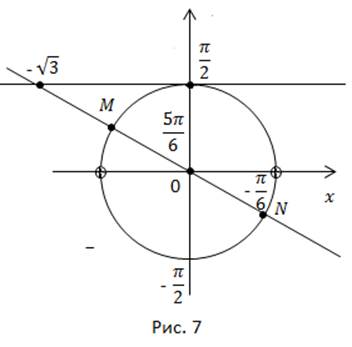
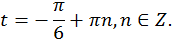
Воз­мож­на и дру­гая за­пись: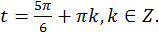

Про­ил­лю­стри­ру­ем ре­ше­ние на гра­фи­ке (рис. 8).

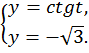
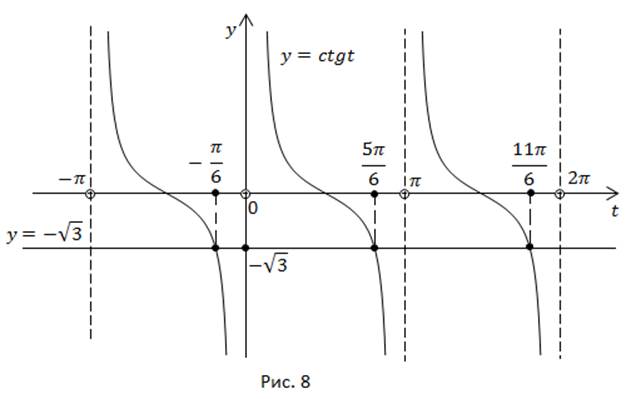
Ответ: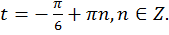

6. Решение простейших тригонометрических уравнений:

Рас­смот­рим часто встре­ча­ю­щи­е­ся про­стей­шие урав­не­ния:

a) 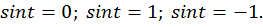Рис. 9.

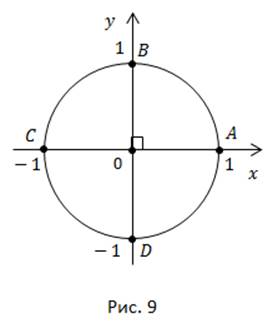
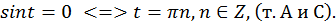
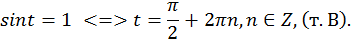
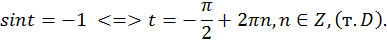
b)