Распределённость терминов в категорических суждениях
Терминами категорического суждения называются субъект и предикат этого суждения. Термин распределён, если он рассматривается в данном суждении во всём объёме, т.е., если он полностью включается в объём другого понятия или полностью исключается из него. В противном случае термин не распределён.
В суждениях (А) субъект распределён, а предикат, как правило, не распределён. В случае, когда термины суждения являются тождественными понятиями, они оба распределены.
В суждении (I) квантор "некоторые" показывает, что субъект данного вида суждения всегда не распределён, т.к. только часть его объёма относится к предикату. Предикат, как правило, также не распределён, кроме случаев, когда объём предиката полностью входит в объём субъекта и, таким образом, предикат оказывается распределён. Этот вид суждений, где объём предиката меньше объёма субъекта, называют частными выделяющими суждениями (в отличие от общих выделяющих, где Р > S ).
Суждение (Е) состоит из терминов, которые благодаря квантору "ни одно" и отрицательной связке, не имеют общих элементов объёмов. Другими словами, объём субъекта полностью исключается из объёма предиката, и наоборот – это означает, что оба термина распределены.
Суждение (О) имеет кванторное слово "некоторые", т.е. объём субъекта мыслится только частично. Предикат в этом суждении, напротив, распределён, поскольку все элементы его объёма исключены из мыслимой части объёма субъекта.
Из всех рассмотренных случаев можно вывести следующее обобщающее правило: субъект всегда распределён в общих суждениях и не распределён в частных; предикат всегда распределён в отрицательных суждениях, а в утвердительных он распределён тогда, когда объём предиката меньше или совпадает с объёмом субъекта (Р £S).
Для того чтобы установить или проверить распределённость субъекта и предиката, можно изобразить их отношение кругами Эйлера и выделить (заштриховать) те части объёмов терминов, которые соединяются утвердительными или исключаются отрицательными высказываниями.
Отношения между простыми категорическими суждениями по истинности. Логический квадрат
Отношения суждений по истинности позволяют определять противоположные суждения, суждения, несовместимые с ранее высказанными и, наоборот, необходимо следующие из уже доказанных.
Если в одном суждении встречается хотя бы один термин, не входящий в другое суждение, то такие два суждения несравнимы.Суждения сравнимы, если их термины совпадают.
Сравнимые суждения совместимы, если они могут быть одновременно истинны, и несовместимы, если не могут быть вместе истинными. В свою очередь, отношения совместимости делятся на отношения подчинения (субординации) и субконтрарности, а отношения несовместимости – на отношения противоположности (контрарности) и противоречия (контрадикторности). Наглядно и системно эти отношения представлены в логическом квадрате.
Подчинение (субординация). Частные суждения подчиняются общим. Это значит:
а) Истинность подчиняющего общего суждения влечёт истинность подчинённого частного, но не наоборот.
б) Ложность подчинённого суждения влечёт ложность подчиняющего, но не наоборот.
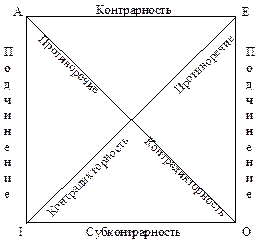
| |
а) Если одно из субконтрарных суждений ложно, то другое необходимо истинно.
б) Из истинности одного из субконтрарных суждений следует неопределённость истинности другого.
Противоположность (контрарность).Отношение общих суждений (А) и (Е) состоит в том, что они не могут быть одновременно истинными, но бывают оба ложны.
а) Из истинности одного суждения следует ложность другого.
б) Из ложности одного суждения следует неопределённость относительно истинности другого.
Противоречие (контрадикторность).Отношение пар суждений (А) – (О) и (Е) – (I) подчиняется закону исключённого третьего, т.е. истинность одного из них влечёт необходимо ложность другого, и наоборот, ложность одного – истинность другого.
Сложные суждения
Сложные суждения – это суждения, состоящие из двух и более простых суждений, соединённых логическими постоянными (союзами).
Логические константы (союзы) определяют виды сложных суждений и обозначаются специальными символами:
- конъюнкция "и" (Ù) образует соединительное суждение (а Ù b);
- дизъюнкция "или" (v) образует разделительное суждение (а v b);
- строгая дизъюнкция "либо" (Ú) образует исключающе-разделительное суждение (а Ú b);
- импликация "если..., то" (®) образует условное суждение (а® b);
- эквиваленция "тогда и только тогда, когда" (º) образует равнозначное суждение (а º b);
- отрицание "неверно, что" образует отрицательное сложное суждение ( ā ) или ( a).
Логические союзы могут соединять любое количество суждений; истинность сложного суждения при этом будет зависеть только от вида констант и истинности простых составляющих его суждений и не будет зависеть от содержания (смысла), количества и качества этих суждений. Истинность и ложность сложных суждений устанавливается при помощи так называемых "таблиц истинности", в которых последовательно фиксируется истинность сложного итогового высказывания по мере присоединения элементарных составляющих. В современных условиях вычисление истинности сложных высказываний производится машинным способом.
Соединительное суждение аÙ b (конъюнкция)
| а | b | a Ù b |
| и | и | и |
| л | и | л |
| и | л | л |
| л | л | л |
Правило: конъюнкция истинна тогда и только тогда, когда истинны все входящие в неё простые суждения (конъюнкты).
