Натуральное исчисление высказываний.

Определение 1 (исчисления).Исчислениями называются теории, содержание которых фиксируется на специально созданном символическом языке, а все допустимые преобразования (в том числе и рассуждения) строятся как преобразования одних последовательностей символов в другие их последовательности.

Замечание. В натуральном исчислении преобразования формул строятся только на основе правил. Алфавит языка этого исчисления и определение правильно построенной формулы совпадает с алфавитом и понятием формулы логики высказываний, заданных выше. А понятиям логического закона и логического следования здесь вводятся синтаксические аналоги – понятие теоремы и понятие выводимости.

Для построения натурального исчисления для логики высказываний необходимо:

- задать правила вывода;

- сформулировать понятия вывода и выводимой формулы.

Правила вывода.

Правила вывода делятся на правила введения логических связок и удаление логических связок и. В формулировке правил «В:» сокращает слово «Введение», а «У:» - «Удаление».

В: Ú	А	В: Ú	В	У: Ú	Г, А Ú В;	Г, А├ С	Г, В├ С
	А Ú В		А Ú В			Г├ С
В: Ù	А, В	У: Ù	А ÙВ	У: Ù	А Ù В
	А Ù В		А		В

В:É	Г, А ├В	У: É	А, А É В
	Г ├ А É В		В

У:~	~~ А		В: ~	Г, А ├ В; Г, А ├ ~В
	А			Г├ ~В

У(слабое): ~	А, ~А
	В

Определение 2 (вывода). Выводом называется непустая конечная последовательность формул, в которой любая формула является либо посылкой, либо формулой полученной из предыдущих по правилам вывода.

Определение 2. (выводимой формулы). Последняя формула в выводе называется выводимой формулой.

Комментарии к правилам вывода. Над чертой правила - посылки, под чертой правила – заключение. Правила делятся на однопосылочные (над чертой пишется одна формула) и двухпосылочные (над чертой пишутся две формулы). Правила делятся на правила прямого вывода и правила косвенного вывода. В правилах косвенного вывода в посылках используется знак выводимости «├», который означает, что строятся вспомогательные выводы. Правило В: ®предполагает доказательство теоремы дедукции.

Тема 3. Традиционная теория силлогических рассуждений

Суждение, виды и структура суждений, отношения между суждениями. Логический квадрат. Алфавит и семантика традиционной силлогистики. Непосредственные и опосредованные рассуждения. Простой категорический силлогизм и его характеристики. Сложные и сокращенные силлогизмы. Иные виды силлогистических рассуждений.

Понятие суждения. Суждение и предложение.Наряду с понятиемк числу основных форм мышления относится суждение, которое является обязательным элементом всякого познания, в особенности связанного с процессами рассуждения, осуществлением выводов и построением доказательств. В суждении фиксируются результаты познания отдельных объектов, их классов, положение дел в мире. Можно сказать, что в суждении утверждается наличие или отсутствие действительного положения дел.

Языковой формой выражения суждений является повествовательное предложение и риторический вопрос. Суждение может оцениваться как истинное или ложное. Суждение является истинным, если описываемое в нем положение дел действительно имеет место, в противном случае оно ложно. В мысли этого типа содержится, с одной стороны, описание или обозначение предметов, ситуаций или событий, и с другой – утверждение или отрицание наличия у них той или иной характеристики. Таким образом, суждение – это мысль, в которой утверждается наличие или отсутствие свойств у предметов, отношений между предметами и связей между ними.Суждения бывают простыми и сложными. Простыминазываются суждения, в которых нельзя выделить часть, в свою очередь являющуюся суждением. В простом суждении утверждается наличие или отсутствие каких-либо характеристик у какого-нибудь отдельного предмета, у некоторых предметов или у всех предметов некоторого класса. Например: "Логика – теоретическая наука", "Ничто не вечно под Луной", "Хорошее начало – половина дела".

Сложными являются суждения, в которых можно выделить часть, в свою очередь являющуюся суждением. Например: "Я вышел на улицу и сломал ногу". Сложные суждения образуются из простых, а также других сложных суждении с помощью логических союзов: "и", "или", "если ..., то ...", "если и только если", "неверно, что ...".

Логические союзы имеют ряд особенностей по сравнению с грамматическими союзами. Грамматические союзы, связывая между собой простые предложения и образуя сложные, обеспечивают смысловое единство целого сложного предложения. Это достигается использованием грамматических правил того или иного языка. При этом мы отвлекаемся от характеристики истинности или ложности как простых предложений, так и получившегося сложного предложения. Для нас важно, чтобы полученное сложное предложение представляло собой некое смысловое единство.

Логические же союзы представляют собой связи между суждениями. А поскольку суждение как форма мышления может быть истинным или ложным, мы отвлекаемся от смысловых связей между мыслями, выражаемыми суждениями, и учитываем лишь логические значения – истинность и ложность суждений.

По характеру связи между простыми суждениями сложные суждения делятся на соединительные, разделительные, условные, эквивалентности и отрицания.

Соединительнымназывается суждение, образованное из двух других суждений с помощью логического союза "и".

Разделительным называется суждение, образованное из двух других суждений с помощью логического союза "или".

Условнымназывается суждение, образованное из двух других суждений при помощи логического союза "если... ", "то ....".

Суждение эквивалентности образуется из двух других суждений с помощью логического союза "если, и только если...".

Суждения отрицания образованы с помощью логического союза "не" или "неверно, что...".

Логическая структура сложных суждений и выводы, построенные на основе их структуры, изучается в классической логике высказываний.

Простые суждения и их виды.Основными, структурными элементами простого суждения являются: один или несколько субъектов суждения (логических подлежащих). Субъектомявляется термин, выражающий понятие и представляющий предметы, о которых нечто утверждается или отрицается; это то, что мы хотим охарактеризовать в этом суждении. Другим структурным элементом простого суждения является предикат (логическое сказуемое) – часть суждения, выражающая то, что утверждается или отрицается о предметах, выражаемых субъектом, это сама характеристика субъекта. Таким образом, чтобы ответить на вопрос, что является субъектом суждения, необходимо ответить на вопрос, что или кого хотят охарактеризовать в этом суждении? А для того, чтобы найти предикат, надо ответить на вопрос, как хотят охарактеризовать субъекта или субъекты?

По характеру предиката простые суждения делятся на атрибутивные, суждения об отношениях и суждения существования.

В атрибутивных суждениях выражается принадлежность или отсутствие у предметов каких-либо свойств.

В суждениях об отношениях утверждается, что определенные отношения имеют или не имеют место между парами, тройками и т.д. субъектов.

В суждениях существования выражается факт существования или не существования предмета мысли, т.е. субъекта.

Так, примерами атрибутивных суждений являются: "Все студенты нашей группы сдали зачет по логике", "Все металлы электропроводны", "Земля имеет форму шара", "Ни один дельфин не является рыбой". В каждом атрибутивном суждении есть субъект (S), предикат (P) и связка, (которая иногда просто подразумевается). В некоторых атрибутивных суждениях имеются еще и так называемые кванторные (количественные) слова: "некоторые", "все", "ни один". Это связано с тем, что по характеру субъектов атрибутивные суждения могут быть единичными, частными и общими. В единичном суждении субъектом является термин, обозначающий единичный предмет, и обычно субъект такого суждения – единичное имя: "Маршал Г. Жуков – великий полководец Великой Отечественной войны". Структура этого суждения – Sсуть Р. Суждение же "Некоторые немецкие философы были идеалистами" является частным, поскольку в нем выражается принадлежность признака "быть идеалистом" некоторым предметам из рассматриваемого множества, что подчеркивается наличием кванторного слова "некоторые". Структура этого суждения – некоторые S суть Р. Суждение "Все планеты Солнечной системы вращаются вокруг Солнца" является общим, т.к. в нем выражается принадлежность свойства "вращаться вокруг Солнца" всем и каждому предмету рассматриваемого множества. Структура этого суждения — Все Sсуть Р.

Кроме того, что атрибутивные суждения являются единичными частными и общими,что определяется кванторными словами, они различаются и связками. В суждениях, выражающих наличие свойств у предметов и, которые называются утвердительными, употребляется связка "суть" ("есть", "является"). Например: "Рыбы дышат жабрами". Логическая форма::Все Sсуть Р. Если же в суждении выражается отсутствие свойств у предмета или предметов, такие суждения называются отрицательными, в структуре суждения употребляется связка "не суть" ("не есть", "не является"). Например: "Демокрит не является идеалистом" (Sне суть Р), "Ни одна звезда не является обитаемой" (Ни один Sне суть Р).

Примерами суждений об отношениях являются: "Москва больше Таганрога", логическая форма: а R в (где а и в – субъекты, а R – предикат). "Таганрог находится между Ростовом-на-Дону и Мариуполем". Логическая форма этого суждения: R (а, в, с), где а, в, с – субъекты, и R – трехместный предикат.

Что касается суждений существования, то примерами таковых являются: "Мышление без языка не существует", "Материя существует", "Нет счастья в жизни" и т.д.

Категорические суждения и их виды.При решении вопроса о правильности и неправильности некоторых типов рассуждений, а также в связи с традицией в логике используется подвид простых атрибутивных суждений, который учитывает объединенную качественно-количественную характеристику простых атрибутивных суждений, которые называются категорическими и к ним относятся: общеутвердительные, частноутвердительные, общеотрицательные и частноотрицательные.

Общеутвердительныесуждения имеют логическую форму.

Все S суть Ри обозначаются латинской буквой А.

Частноутвердительныеимеют логическую форму.

Некоторые Sсуть Ри обозначается латинской I.

Общеотрицательные суждения имеют логическую форму

Ни один S не суть Р и обозначаются латинской Е.

Частноотрицательныеимеют логическую форму.

Некоторые S не суть Р и обозначаются латинской О.

Например: "Некоторые птицы не улетают зимой на юг." Это суждение О. "Все жидкости – упруги" – суждение А, "Ни один человек не должен страдать за правду" – суждение Е." "Некоторые водоемы являются пресноводными" – суждение I.

Распределенность терминов в простых категорических суждениях.Понятие распределенности или нераспределенности термина категорического суждения – его субъекта или предиката – указывает на наличие или отсутствие информации, вычленяемой из анализа суждения, обо всех или не обо всех предметах класса, представителем которого является данный термин. Другими словами, распределенность терминов есть знание об отношении субъекта и предиката, которое мы получаем в результате анализа структуры того или иного суждения.

На распределенность или нераспределенность субъекта указывает количественная характеристика суждения ("все", "Некоторый"). Распределенность или нераспределенность предиката зависит от качества суждения.

Так, в утвердительных суждениях мы не можем иметь полной инфор-мации о предметах Р, так как в этих суждениях говорится о некотором тождестве всех или некоторых предметов Sс какими-то предметами Р.

Но в отрицательных суждениях мы имеем точную информацию о том, что все или некоторые предметы Sне тождественны ни с одним из предметов Р. Поэтому мы можем сказать, что термин называется распределенным, если его объем полностью входит в объем другого термина или полностью исключается из него. Термин называется нераспределенным, если его объем лишь частично включается или исключается из объема другого термина.

Так, в суждении типа А – "Все S суть Р" – объем Sполностью входит в Р, и, следовательно, S –распределен, а Р лишь частично совпадаетс S, следовательно, Р – нераспределен. Посредством круговых схем это выглядит следующим образом:

Такая распределенность терминов характерна и для единичных утвердительных суждений.

В суждениях типаI –"Некоторые Sсуть Р "- и Sи Pнераспределены. Графически:

В суждениях типа Е – "Ни один S не суть Р"- и S и Р распределены также, как и в единичных отрицательных суждениях. Графически:

В суждениях типа – "Некоторые S не суть Р "- S нераспределен, т.к. не все S входят в Р, а Р распределен, т.к. в этом случае мыслятся все предметы Р и ни один из них не входит в S. Графически:

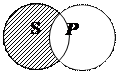Таким образом, правила распределенности терминов в категорических суждениях заключаются в следующем:

I. Субъекты распределены в общих и нераспределены в частных суждениях.

2. Предикаты распределены в отрицательных и нераспределены в утвердительных суждениях.

Логические отношения между категорическими суждениями.Между определенного рода категорическими суждениями существуют логические отношения, которые основаны на их сходстве по содержанию. Это сходство определяется одинаковостью субъекта и предиката и различием в количестве и качестве суждений. Такие суждения называются сравнимыми.

Если два суждения имеют различные субъекты или предикаты, то установить логические отношения между ними не представляется возможным. Отношения между сравнимымисуждениями изображаются посредством так называемого "логического квадрата":

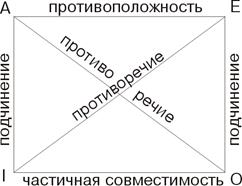
Два сравнимых суждения могут быть совместимыми и несовместимыми.

Совместимыми являются два суждения, которые одновременно могут быть истинными. Несовместимыми являются два суждения, которые не могут быть одновременно истинными.

Отношения совместимости – эквивалентность, частичная совместимость (субконтрарность) и подчинение. Отношениями несовместимости являются: противоположность (контрарность) и противоречие (контрадикорность).

Отношения эквивалентности в логическом квадрате не иллюстрируются, т.к. эти суждения имеют одинаковые субъекты, предикаты, качество и количество, а различия могут быть чисто языкового характера.

Например, квантор существования может быть выражен в языке как "некоторые", "многие", "как правило", "существует", или же суждения зафиксированы на разных языках. Эквивалентными суждениями являются: "Многие юристы являются адвокатами" – "Некоторые юристы адвокаты" или же "Многие студенты являются спортсменами" -"Some students are sportsmen". В отношении подчинения находятся суждения А и I, Е и 0. Причем, общие суждения (А и Е) являются подчиняющими, а частные ( Iи0 ) – подчиненными.

Для этого отношения характерны две зависимости:

1.При истинности общего (подчиняющего) суждения истинным будет и частное (подчиненное) суждение. То есть, если А истинно, то I тоже истинно, и если Е истинно, то Овсегда будет истинным.

2. При ложности частного суждения общее всегда будет ложным. Так, если подчиненное I – ложно, то и подчиняющее А будет тоже ложно; если 0 -ложно, таковым будет и Е.

В остальных случаях возникает неопределенность: при ложности общего частное может быть и истинным, и ложным, а при истинности частного, общее также может быть и истинным, и ложным.

Отношение частичной совместимости (субконтрарности) характерно для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными. Так, если I – ложно, то 0 обязательно должно быть истинным; если 0 – ложно, то I будет истинным. Но если I – истинно, то 0 может быть или истинным или ложным;и если 0 – истинно, то I может быть или истинным или ложным.

Суждения А и Е находятся в отношении противоположности (контрарности). Эти суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Если истинно суждение А, то Е будет ложным и наоборот если Е – истинно, то А – ложно. Но если А – ложно, то Е будет или истинным или ложным;и если Е – ложно, то А может быть или истинным или ложным.

В отношении противоречия (контрадикторности) находятся суждения А и 0, и Е и I. Эти суждения не могут быть одновременно истинными и одновременно ложными. Если одноиз них истинно, то другое обязательно должно быть ложным и наоборот. Так, если А – истинно, то 0 – ложно. Если А ложно, то 0 – истинно. Если О – истинно, то А – ложно. Если О – ложно, то А – истинно. Если Е – истинно, то I – ложно. Если Е – ложно то I – истинно. Если I – истинно, то Е – ложно, и если I – ложно, то Е – истинно.

Применение этих правил, мы рассмотрим в параграфе "Умозаключения на основе отношений между суждениями по логическому квадрату".