Парный критерий Т – Вилкоксона
Для решения задач, в которых осуществляется сравнение двух рядов чисел психолог может использовать парный критерий Т - Вилкоксона. Этот критерий применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, т. е. он позволяет установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом.
Критерий Т основан на ранжировании абсолютных величин разности между двумя рядами выборочных значений в первом и втором эксперименте (например, до и после какого-либо воздействия). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем наряду с общей суммой рангов находится отдельно сумма рангов, как для положительных, так и для отрицательных сдвигов. Если интенсивность сдвига в одном направлении оказывается большей, то и соответствующая сумма рангов также оказывается больше. Этот сдвиг называется типичным, а противоположный, меньший по сумме рангов сдвиг – нетипичным. Эти два сдвига оказываются дополнительными друг другу. Критерий Т - Вилкоксона базируется на величине нетипичного сдвига, который называется Т 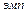
Пример: Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений.
Для решения этой задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В табл. 5 приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т - Вилкоксона.
Таблица 5
| № испытуемых п/п | До коррек ционной работы | После коррек ционной работы | Сдвиг (значение разности с учетом знака) | Абсолютные величины разностей | Ранги абсолютных величин разностей | Символ нетипичного двига |
| -2 | 10,5 | |||||
| -1 | 6,5 | |||||
| +1 | 6,5 | * | ||||
| -8 | ||||||
| -11 | ||||||
| -20 | ||||||
| -18 | ||||||
| -1 | 6,5 | |||||
| +1 | 6,5 | * | ||||
| -22 | ||||||
| -1 | 6,5 | |||||
| -2 | 10,5 | |||||
| -6 | 13,5 | |||||
| -4 | ||||||
| -1 | 6,5 | |||||
| +6 | 13,5 | * | ||||
| Сумма | Т 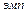 = 26,5 = 26,5 |
Обработка данных по критерию Т – Вилкоксона осуществляется следующим образом:
1. В четвертый столбец таблицы вносятся величины сдвигов с учетом знака. Их вычисляют путем вычитания из чисел третьего столбца соответствующих чисел второго столбца.
2. В пятом столбце в соответствие каждому значению сдвига ставят его абсолютную величину.
3. В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце.
4. По формуле: 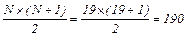 подсчитывают сумму рангов. В нашем примере она составляет:
подсчитывают сумму рангов. В нашем примере она составляет:
12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + 10,5 + 13,5 + 12 + 6,5 + 13,5 +2 = 190
5. Проверяют правильность ранжирования на основе совпадения сумм рангов полученных двумя способами. В нашем случаи обе величины совпали, 190 = 190, следовательно, ранжирование проведено правильно.
6. Любым символом отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае это три положительных сдвига.
7. Суммируют ранги нетипичных сдвигов. Это и будет искомая величина Т 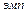 . В нашем случае эта сумма равна: Т
. В нашем случае эта сумма равна: Т 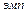 = 6,5 + 13,5 + 6,5 = 26,5.
= 6,5 + 13,5 + 6,5 = 26,5.
По табл. 15 приложения 6 определяют критические значения Т 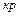 для n = 19.
для n = 19.
Нужная нам строка табл. 15 из приложения 6 выделена ниже в табл. 7.
Таблица 6
| n | P | |
| 0,05 | 0,01 | |
Поскольку в нашем случаи основной, типичный сдвиг – отрицательный, то дополнительный, «нетипичный» сдвиг будет положительным и на уровне значимости в 5% сумма рангов таких сдвигов не должна превышать числа 53, а при уровне значимости в 1% не должна превышать числа 38. Представим сказанное выше следующим образом:
Т 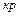 = 53 для P
= 53 для P 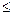 0,05
0,05
38 для P 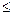 0,01
0,01 
Строим «ось значимости»:
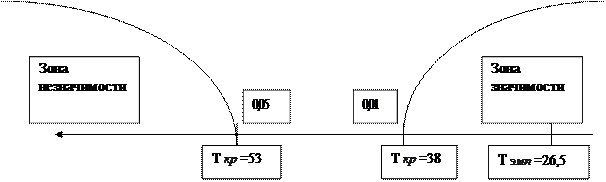
Анализ «оси значимости» показывает, что полученная величина Т 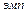 попадает в зону значимости. Следовательно, можно утверждать, что зафиксированные в эксперименте изменения не случайны и значимы на 1% уровне. Таким образом, психолог может говорить о том, что применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы, следовательно, оказывает положительное влияние на развитие внимания школьников.
попадает в зону значимости. Следовательно, можно утверждать, что зафиксированные в эксперименте изменения не случайны и значимы на 1% уровне. Таким образом, психолог может говорить о том, что применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы, следовательно, оказывает положительное влияние на развитие внимания школьников.
Для применения критерия Т – Вилкоксона необходимо соблюдать следующие условия:
1. Измерение может быть проведено во всех шкалах, кроме номинальной.
2. Выборка должна быть связной.
3. Число элементов в сравниваемых выборках должно быть равным.
4. Критерий Т - Вилкоксона может применяться при численности выборки от 5 до 50 (на большую величину не рассчитана таблица достоверности).
