Основные законы классической логики высказываний. Схемы правильных выводов традиционной логики в языке логики высказываний.

· При практическом использовании логики, т. е. при осуществлении и анализе рассуждений в естественном языке, каждый раз применять процедуру построения таблиц истинности было бы делом громоздким. Поэтому имеет смысл выделить наиболее важные и часто встречающиеся в практике аргументации логические законы и способы правильных рассуждений.

Выделим наиболее известные законы логики высказываний. При этом будем указывать не сами формулы, а их типы или, как говорят, схемы тождественно-истинных формул.

Выражения, содержащие метапеременные, пробегающие по формулам объектного языка и репрезентирующие классы формул этого языка, называют схемами формул.

Если схема формул репрезентирует такой класс, каждая формула которого является законом логической теории, то ее называют схемой законов данной теории.

1. Закон тождества:

А –>А.

2. Закон противоречия:

(А & А).

3. Закон исключенного третьего:

AvA.

· Схемы правильных выводов.

11. Аксиоматическое построение исчисления высказываний. (формальная аксиоматическая система).
Если будет понятнее, то вопрос можно заменить так: Аксиоматическое построение в логике высказываний.

Форма́льная систе́ма (форма́льная тео́рия, аксиоматическая теория, дедуктивная система) — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.

Формальная система — это совокупность абстрактных объектов, не связанных с внешним миром, в которой представлены правила оперирования множеством символов в строго синтаксической трактовке без учёта смыслового содержания, то есть семантики.

Для аксиоматического исчисления для логики высказываний необходимо:

1) Создать (определить) формальный язык и все сопутствующие понятия типа: правильно построенная формула, подформула и т.д.

2) Указать определения доказательства и доказуемой формулы на основании п3.

Доказательство – такая последовательность формул, каждая из которых является либо АКСИОМОЙ, либо формулой, полученной из предыдущих по одному из правил вывода данной аксиоматической системы.

Доказуемая формула – формула доказуема, если построено доказательство, в которой эта формула является последней.

3) Определить аксиомы, указать правила доказательства (вывода).

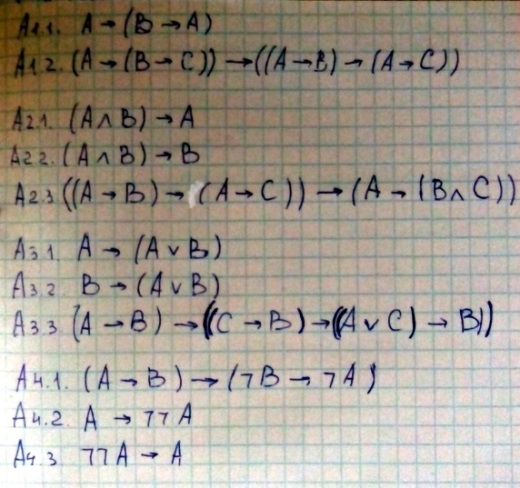
Правила вывода:

a) Используем правило MP (modus ponens)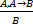

b) Используем правило подстановки (простую формулу А в формуле можно заменить на любую ДОКАЗУЕМУЮ формулу)

4)Сформулировать относительно формальной системы метатребования: корректность и полнота.

- Произвольная логическая теория Т называется семантически непротиворечивой, если любая доказуемая в ней формула является тождественно-истинной (общезначимой)

- Логическая теория Т называется синтаксически непротиворечивой, если в ней невозможно доказать некоторую формулу и отрицание этой формулы.

- Логическая теория Т считается семантически полной, если в ней доказуема любая тождественно-истинная (общезначимая) формула.

- Логическая теория Т, сформулированная с помощью схем аксиом, считается синтаксически полной (максимальной), если к ней нельзя присоединить без противоречия ни одной недоказуемой в ней схемы формул, т. е.