Раздел 4. Расчет прогиба плиты

Расчет изгибаемых элементов по прогибам производят из условия:

f < f _ult

где f – прогиб элемента от действия внешней нагрузки

f _ult – значение предельно допустимого прогиба

При действии постоянных, длительных и кратковременных нагрузок прогиб плиты во всех случаях не должен превышать 1/200 пролета.

Для свободно опертой плиты максимальный прогиб определяется:

f = S * l² *( ) _max, где S – коэффициент, зависящий от расчетной схемы и вида нагрузки; при действии равномерно распределенной нагрузки S = 5/48 , при двух равных моментах по концам плиты от силы обжатия S = 1/8

( ) _max - полная кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб.

Полную кривизну изгибаемых элементов определяют для участков без трещин в растянутой зоне по формуле:

= ( )₁ + ( )₂ - ( )₃ , где

( )₁ – кривизна от непродолжительного действия кратковременных нагрузок

( )₂ - кривизна от продолжительного действия постоянных и длительных нагрузок

( )₃ - кривизна от непродолжительного усилия предварительного обжатия Р₍₁₎ , вычисленного с учетом только первых потерь, т.е. при действии момента

М = Р₍₁₎ * е _о.р.

Кривизну элемента на участке без трещин определяют по формуле:

= , где М - изгибающий момент от внешней нагрузки

- момент инерции приведенного сечения

- модуль деформации сжатого бетона, определяющийся по фор-ле:

, где - коэффициент ползучести бетона

= 2,8 , где коэффициент принимается в зависимости от средней влажности воздуха и класса бетона В15-В25.

Прогиб определяется с учетом действия только постоянных и временных длительных нагрузок.

( )₂ = = ____ 1/см, где

– изгибающий момент от действия постоянных и длительных нагрузок.

= = = 7,24 * МПа = 7,24 * кН/см²

Кривизна от кратковременного выгиба при действии усилия предварительного обжатия

( )₃ = = _____ 1/см

Запас жесткости плиты оцениваем по ее прогибу, учитывая только постоянную и длительную нагрузки.

f = ( ) * = ____ см < f _ult

Допустимый прогиб f _ult = = ____ см.

Кроме того, может быть учтена кривизна ( )₄ , обусловленная выгибом элемента вследствие усадки и ползучести бетона в стадии изготовления от неравномерного обжатия по высоте сечения плиты.

( )₄ = , где

- значения, равные сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона.

Напряжения в уровне крайнего сжатого волокна:

* ( h – y_o ) = ____ кН / см² = МПа

– усилие от предварительного обжатия с учетом полных потерь

Значит, в верхнем волокне в стадии предварительного обжатия возникает растяжение, поэтому принимаем = 0

Проверяем, образуются ли, в верхней зоне трещины в стадии предварительного обжатия:

, где

– значение ( верхнего волокна )

- расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от грани элемента

, - усилие обжатия с учетом первых потерь и его эксцентриситета.

γ =1,25 - для двутаврового симметричного сечения

= = ____ см, Р₍₁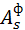₎ = ( ) * = ____ кН

Передаточная прочность назначается не менее 15МПа и не менее 50% принятого класса бетона. Тогда получим:

=1,1 МПа = 0,11 кН / см²

= ____кН / см² = кН/ м > 0 , следовательно трещины в верхней зоне в стадии предварительного обжатия не образуются. В нижней зоне в стадии эксплуатации трещин также нет.

Для элементов без трещин сумма кривизн ( )₃ + ( )₄ принимается не менее кривизны от усилия предварительного обжатия при продолжительном его действии:

= = 7,24*10³ МПа = 7,24 * 10² кН/см²

( )₃ = = ___ 1/см

__ МПа = __ кН/ см²

10⁴ кН/ см²

( )₄ = = __ 1/см

( )₃ + ( )₄ = ___ 1/см

Это значение больше, чем кривизна от усилия предварительного обжатия при продолжительном его действии ( ( )₂ ).

Таким образом, прогиб плиты с учетом выгиба:

f = ( ) * = ____ см < f _ult