Законы логики и их материалистическое понимание

Закон тождества

Закон тождества является одним из законов правильного мышления, соблюдение этого закона гарантирует определен­ность и ясность мышления. Закон формулируется так: «В процес­се определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе». В математической логике за­кон тождества выражается следующими формулами:

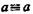(в логике высказываний) и 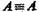(в логике классов, в которой классы отождествляются с объемами понятий).

Схема закона тождества: 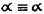. Если в нее вместо 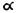подставляются высказывания, то будет 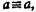а если подставляются понятия, то будет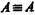

Тождество есть равенство, сходство предметов в каком-либо отношении. Например, все жидкости теплопроводны, упруги. Каждый предмет тождествен самому себе. В объективной реаль­ности тождество существует в связи с различием. Нет и не может быть двух абсолютно тождественных вещей (например, двух листочков дерева, близнецов и т. д.). Одна и та же вещь вчера и сегодня и тождественна, и различна. Так, например, внешность человека изменяется с течением времени, но мы его узнаем и считаем одним и тем же человеком. Абстрактного, абсолют­ного тождества в действительности не существует, оно означало бы прекращение развития. Но при известных условиях (в опреде­ленных границах) мы можем отвлечься от существующих раз­личий и фиксировать свое внимание только на тождестве пред­метов или их свойств.

В мышлении закон тождества выступает в качестве норматив­ного правила (принципа). Он означает, что в процессе рассужде­ния нельзя подменять одну мысль другой, одно понятие другим. Нельзя тождественные мысли выдавать за различные, а различ­ные — за тождественные.

Например, тождественными по объему будут такие три поня­тия: ученый, по инициативе которого основан Московский уни­верситет; ученый, сформулировавший принцип сохранения материи и движения; ученый, ставший с 1745 г. первым русским академиком Петербургской Академии наук, так как они обозна­чают одного и того же человека (М. В. Ломоносова), но дают различную информацию о нем.

Нарушение закона тождества приводит к двусмысленности, что можно видеть, например, в следующих рассуждениях: «Ноздрев был в некотором отношении исторический человек. Ни на одном собрании, где он был, не обходилось без истории» (Н. В. Гоголь). «Стремись уплатить свой долг, и ты достигнешь двоякой цели, ибо тем самым его исполнишь» (Козьма Прут­ков). Игра слов в этих примерах построена на употреблении омонимов.

В мышлении нарушение закона тождества проявляется тогда, когда человек выступает не по обсуждаемой теме, произвольно подменяет один предмет обсуждения другим, употребляет тер­мины и понятия не в том смысле, в каком это принято, не предупреждая об этом. Например, идеалистом иногда считают человека, верящего в идеалы, живущего ради высокой цели, а материалистом — человека меркантильного, стремящегося к наживе, к личному обогащению и т. д. Ф. Энгельс писал о понимании материализма филистером (т. е. обывателем, ме­щанином): «Под материализмом филистер понимает обжорство, пьянство, похоть, плотские наслаждения и тщеславие, корысто­любие, скупость, алчность, погоню за барышом и биржевые плутни, короче — все те грязные пороки, которым он сам преда­ется втайне»¹. В философии же, как известно, материализм — это направление которое первичным считает материю, а вто­ричным — сознание.

Иногда в ходе дискуссий спор по существу подменяют спором о словах. Иногда люди говорят о разных вещах, думая, что они имеют в виду одного и того же человека либо одну и ту же вещь или событие. Логические ошибки часто совершают при употреб­лении омонимов, т. е. слов, имеющих два значения («следствие», «материя», «содержание» и др.). Например, «Ученики прослушали разъяснения учителя», «Из-за рассеянности шахматист не раз на турнирах терял очки». Иногда ошибка возникает при использова­нии личных местоимений «она», «оно», «они», «мы» и т. д., когда приходится уточнять: «Кто — он?» или «Кто — она?». В резуль­тате отождествления различных понятий возникает логическая ошибка, называемая подменой понятия.

При нарушении закона тождества возникает и другая ошибка, называемая подменой тезиса. В ходе доказательства или опровер­жения выдвинутый тезис часто умышленно или неосознанно под­меняется другим. В научных и иных дискуссиях это проявляется в приписывании оппоненту того, чего он не говорил. Такие приемы ведения дискуссий недопустимы.

Прием подмены тезиса: вместо одного вопроса стремятся искусно подсунуть другой, чтобы отвлечь в нужный момент внимание читателя, наговорив кучу к делу не относящихся вещей, приписать противнику то, чего он не говорил, и т. д.

Отождествление (или идентификация) широко используется в следственной практике, например при опознании предметов, людей, сличении почерков, документов, подписей, отпечатков пальцев.

Закон тождества используется в науке, искусстве, в програм­мах для работы ЭВМ, в школьном преподавании, в повседневной жизни.

Такие понятия, как «один», «два», «три» и т. д., связаны с умением различать и отождествлять вещи, а это умение и ис­торически, и логически предшествует умению их считать. Закон тождества «а есть а» (а тождественно а) испокон веков относился людьми к логике.

В действительности абсолютного тождества в изменяющихся предметах нет. Но для того, чтобы отобразить движение в мыс­ли, мы должны прибегнуть к идеализации и упрощению дейст­вительности.

В науках существуют различные виды и модификации тож­дества. Так, например, в математике это равенство, эквивалент­ность (равномощность, равночисленность) множеств, конгруэнт­ность, тождественное преобразование, тождественная подстанов­ка и т. д.; в теории алгоритмов — одинаковость букв, устанав­ливаемая путем абстракции отождествления, равенство алфави­тов (А=В), равенство конкретных слов и т. д.

Равенства обладают свойствами рефлексивности (а = а), сим­метричности (если а = b, то b =а )и транзитивности (если а = b и b = с, то а = с). К равенствам применимо правило замены равно­го равным.

Различие также имеет свои виды и модификации: неравенство, неэквивалентность (неравномощность) множеств и т.д.; в теории алгоритмов — различие букв, неравенство конкретных слов (на­пример, пустого и непустого слова) и др.

Закон непротиворечия

Диалектика исходит из реального онтологического сущест­вования диалектических противоречий во всех предметах дейст­вительности. Но ставя задачу отобразить их, мы должны в силу законов отражения учитывать диалектическую необходимость огрубления при изображении движения мыслью.

Поэтому если предмет А обладает определенным свойством, то в суждениях об А люди должны утверждать это свойство, а не отрицать его. Если же человек, утверждая что-либо, отрицает то же самое или утверждает нечто несовместимое с первым, налицо логическое противоречие. Формально-логические противоречия — это противоречия путаного, неправильного рассуждения. Такие противоречия затрудняют познание мира.

Нельзя смешивать формально-логические противоречия с диалектическими. Закон единства и борьбы противоположно­стей действует всюду, поэтому диалектические противоречия свойственны природе, обществу и мышлению. Борьба проти­воположностей — движущая сила развития природы, общества и мышления.

Древнегреческий философ и ученый Аристотель считал «са­мым достоверным из всех начал» следующее: «...невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении»². Тем самым Аристотель дал логическую формулировку закона непротиворе­чия: «Невозможно что-либо вместе утверждать и отрицать»³. Эта формулировка указывает на необходимость не допускать в своем мышлении и речи формально-противоречивые высказывания, в противном случае мышление будет неправильным.

Мысль противоречива, если мы об одном и том же предмете в одно и то же время и в одном и том же отношении нечто и утверждаем, и отрицаем. Например, «Кама — приток Волги» и «Кама не является притоком Волги». Или: «Лев Толстой — автор романа „Воскресение"» и «Лев Толстой не является авто­ром романа «Воскресение».

Противоречия не будет, если мы говорим о разных предметах или об одном и том же предмете, взятом в разное время или в разном отношении. Противоречия не будет, если мы скажем: «Осенью дождь полезен для грибов» и «Осенью дождь не полезен для уборки урожая» или «Саша Голубев — перворазрядник (по настольному теннису)» и «Саша Голубев не является первораз­рядником (по бегу)», так как предметы мысли в этих суждениях берутся в разных отношениях. Суждения «Саша Голубев не является перворазрядником по бегу» и «Саша Голубев является перворазрядником по бегу» не будут противоречивыми, если они относятся к различному времени, и будут противоречивыми, если они относятся к одному и тому же времени.

Не могут быть одновременно истинными следующие четыре типа простых суждений:

1. «Данное S есть Р» и «Данное S не есть Р».

2. «Ни одно S не есть Р» и «Все S есть Р».

3. «Все S есть Р» и «Некоторые S не есть Р».

4. «Ни одно S не есть Р» и «Некоторые S есть Р».

При этом вторая пара суждений такова, что оба суждения могут быть ложными, например: «Ни один студент не является спортсменом» и «Все студенты являются спортсменами».

Формально-логическое противоречие чаще всего определяется как конъюнкция суждения и его отрицания (а и не-а). Но логичес­кое противоречие может быть выражено и без отрицания; оно имеет место между несовместимыми утвердительными суждени­ями⁴. Таково именно логическое противоречие между суждени­ями, выдвинутыми, с одной стороны, эмпириокритиками , с дру­гой стороны, научными утверждениями естествоиспытателей.

Формально-логическое противоречие возникает тогда, когда пытаются считать истинными два или несколько утвердительных суждений, не совместимых между собой. Не менее распрост­раненной является форма логического противоречия, когда одно­временно утверждается и отрицается одно и то же суждение, т. е. допускается конъюнкция а и не-а. Таким образом, в традицион­ной формальной логике противоречием считается утверждение двух противоположных (как контрарных, так и контрадиктор­ных) суждений об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении. В исчислении высказы­ваний классической двузначной логики закон непротиворечия записывается в виде формулы так: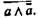

Закон непротиворечия читается так: «Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении». К противоположным суждениям относятся: 1) противные (контрарные) суждения А и Е, которые оба могут быть ложными, поэтому не являются отрицающими друг друга и их нельзя обозначить как а и 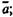2) противоречащие (контрадикторные) суждения А и О, Е и /, а также единичные суждения «Это S есть Р» и «Это S не есть Р», которые являются отрицающими, так как если одно из них истинно, то другое обязательно ложно, поэтому их обозначают а и а.

Формула закона непротиворечия в двузначной классической логике отражает лишь часть содержательного аристотелевс­кого закона 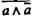непротиворечия, так как она относится только к проти­воречащим суждениям (а и не-а) и не распространяется на против­ные (контрарные) суждения. Поэтому формула 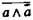неадекватно, не полностью представляет содержательный закон непротиворе­чия. Следуя традиции, мы сохраняем за формулой 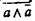название «закон непротиворечия», хотя оно значительно шире, чем формула. Если в мышлении (и речи) человека обнаружено формально­-логическое противоречие, то такое мышление считается непра­вильным, а суждение, из которого вытекает противоречие, от­рицается и считается ложным. Поэтому в полемике при опровер­жении мнения оппонента широко используется метод «приведе­ния к абсурду».

Диалектические противоречия процесса познания иногда вы­ражаются в форме формально-логических противоречий, напри­мер: опровержение гипотезы путем опровержения (фальсифика­ции) следствий, противоречащих опытным фактам или ранее известным законам; выступления докладчика и оппонента; об­винителя и защитника; взгляды людей, придерживающихся кон­курирующих гипотез; рассуждения врача (или врачей при кон­силиуме), получившего клинические анализы, не совместимые с ранее; поставленным диагнозом болезни, и многие другие. Во всех этих и подобных им ситуациях фиксируется несовмести­мость суждения а и не-а, например несовместимость какого-либо суждения а из прежней теории и суждения не-а, выражающего мысль о новом полученном опытном факте, т. е. фиксируется мысль, что суждения а и не-а не могут быть оба истинными, а поэтому их конъюнкция ложна.

Итак, здесь первичным (содержанием) выступает диалектичес­кое противоречие, объективно возникающее в процессе познания и служащее его движущей силой; вторичным же является способ фиксации (выражения) диалектического противоречия в виде ко­нъюнкции двух суждений а и не-а, т. е. в форме формально-­логического противоречия.

Здесь налицо ситуация, по своему типу аналогичная случаю «антиномии-проблемы», когда возникшее диалектическое проти­воречие в познании до момента его разрешения выражается в форме «а и не-а», т. е. принимает облик, оболочку, внешнюю форму формально-логического противоречия, по существу же остается диалектическим, требующим своего разрешения в ходе исследования возникшей проблемы. В результате диалектичес­кого синтеза тезиса и антитезиса получается новое знание, отличающееся и от того, и от другого, а также не являющееся их конъюнкцией. Итак, в мышлении диалектическое противоречие до его разрешения иногда принимает форму (структуру) фор­мально-логического противоречия, а обнаружение последнего сви­детельствует о том, что необходимы дальнейший анализ и исследо­вание возникшей в познании ситуации. Разрешение обнаруженного диалектического противоречия способствует прогрессу познания. Классическим случаем антиномии проблемы является знаме­нитая формулировка познавательной задачи в I томе «Капитала» К. Маркса: «...капитал не может возникнуть из обращения и так же не может возникнуть вне обращения. Он должен возникнуть в обращении и в то же время не в обращении»⁷. Разрешив эту задачу, Маркс раскрывает тайну возникновения прибавочной стоимости: посредствующим звеном на пути к этому раскрытию было установление того, что капитал возникает в производстве, но при непосредственном соучастии обращения⁸.

Закон исключенного третьего

Для двузначной логики онтологическим аналогом этого закона является то, что в предмете указанный признак либо присутствует, либо нет. В книге «Метафизика» Аристотель сформулировал закон ис­ключенного третьего так: «Равным образом не может быть ниче­го промежуточного между двумя членами противоречия, а от­носительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать»⁹.

В двузначной традиционной логике закон исключенного третьего формулируется так: «Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано». Противореча­щими (контрадикторными) называются такие два суждения, в од­ном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается, поэтому они не могут быть оба истинными или оба ложными; одно из них истинно, а другое обязательно ложно. Такие суждения называются от­рицающими друг друга. Если одно из противоречащих суждений обозначить переменной а, то другое следует обозначить а.

Отрицающими являются следующие пары суждений:

1. «Это S есть Р» и «Это S не есть Р» (единичные суждения).

2. «Все S есть Р» и «Некоторые S не есть Р» (суждения А и О).

3. «Ни одно S не ешь Р» и «Некоторые S есть Р» (суждения Е иI).

В отношении противоречащих (контрадикторных) суждений (А и О, Е и I) действует как закон исключенного третьего, так и закон непротиворечия — в этом одно из сходств данных законов.

Различие в областях определения (применения) этих законов в том, что в отношении противных (контрарных) суждений А и Е (например, «Все грибы — съедобны» и «Ни один гриб не является съедобным»), которые не могут быть оба истинными, но могут быть оба ложными, действует лишь закон непротиворечия и не действует закон исключенного третьего. Поэтому сфера действия содержательного закона непротиворечия (контрарные и контрадикторные суждения) шире, чем сфера действия содер­жательного закона исключенного третьего (лишь контрадиктор­ные суждения, т. е. суждения типа а и не-а). Действительно, истинно одно из двух суждений: «Все дома в данной деревне электрифицированы» или «Некоторые дома в данной деревне не; являются электрифицированными»; третьего не дано.

Закон исключенного третьего и в содержательном, и в фор­мализованном виде охватывает один и тот же круг суждений — противоречащие, т. е. отрицающие друг друга суждения.

Содержательные аристотелевские законы непротиворечия и исключенного третьего невыводимы один из другого, так как области определения суждений, к которым они применимы, различны. В силу того что в формализованных законах непротиворечия и исключенного третьего, т. е. в формулах 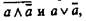области определения пропозициональных переменных (т. е. переменных, обозначающих суждение и его отрицание: 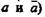оказываются одними и теми же (берутся лишь противоречащие суждения), на основании закона де Моргана, т. е. формулы 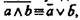закона снятия двойного отрицания, т. е. и закона коммуникативности дизъюнкции, т. е. формулы 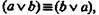в двузначной классической логике путем элементарных эквивалентных преоб­разований из закона непротиворечия можно вывести закон ис­ключенного третьего (и наоборот)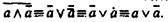

В мышлении закон исключенного третьего предполагает чет­кий выбор одной из двух взаимоисключающих альтернатив.

Специфика действия закона исключенного третьего при наличия «неопределенности» в познании

Как уже отмечалось, объективной предпосылкой действия в мышлении законов непротиворечия и исключенного третьего является наличие в природе, обществе и самом мышлении от­носительно устойчивых состояний предметов (относительного покоя), постоянства и определенности свойств и отношений меж­ду предметами.

Но в природе и обществе происходят изменения, переходы предметов и их свойств в свою противоположность, поэтому нередки переходные состояния, промежуточные ситуации. Неопределенность в самом познании [и в одной из его форм (ступе­ней) — абстрактном мышлении] возникает, во-первых, в резуль­тате отражения «переходных» состояний самих предметов действительности и, во-вторых, в результате неполноты, неточности (на каком-то этапе познания), не вполне адекватного отражения объекта познания в ходе его изучения.

Проанализируем некоторые «переходные» ситуации, встреча­ющиеся в природе, обществе и познании. В природе нестабиль­ность перемещения воздушных потоков, несущих циклоны и антициклоны, вызывает частые изменения погоды, а неуправля­емые стихийные явления природы — землетрясения, наводнения, извержения вулканов, засухи или ливневые дожди — становятся причинами бедствий. Точно предсказать погоду или землетрясе­ние, наводнение и многие другие природные явления пока еще не всегда удается, и эта «неопределенность» нашего познания неред­ко приводит к тому, что люди не могут своевременно подгото­виться к этим нежелательным природным явлениям.

По традиции, идущей от Аристотеля, часть логиков считает, что в ситуациях, относящихся к будущему времени, закон ис­ключенного третьего неприменим, поскольку высказывания: «Завтра необходимо будет морское сражение» и «Завтра необходимо не будет морского сражения» сегодня не истинны и не ложны, но оба неопределенны. Действительно, мы не можем сказать, какое из двух противоречащих суждений: «Через месяц в Ташкенте случится землетрясение» и «Через месяц в Ташкенте землетрясе­ния не случится» — будет истинно, а какое ложно. В то же время солнечное затмение человек может предсказать за сотни лет вперед с точностью до секунды, поэтому в этой жесткой ситуации закон исключенного третьего действует неограниченно, так как мы можем точно указать, какое из двух противоречащих сужде­ний будет истинно: «27 декабря 1998 г. в Москве будет солнечное затмение» и «27 декабря 1998 г. в Москве солнечного затмения не будет», —. хотя оба эти суждения относятся к будущему времени. Поэтому возможность применения закона исключенного третье­го к будущим единичным событиям надлежит каждый раз рас­сматривать конкретно.

В обществе, как и в природе, наряду с определенностью, стабильностью имеются неопределенные ситуации, переходные периоды и состояния. Существуют непредсказуемые, случайные события, например авиационные катастрофы, железнодорожные и автомобильные аварии и т. д. Предсказать какую-то единич­ную катастрофу, как правило, невозможно, поэтому применить в этой ситуации закон исключенного третьего не удается. Можно возразить, что закон исключенного третьего говорит лишь о том, что одно из двух противоречащих суждений истинно, а другое ложно, и третьего не дано, а какое суждение окажется истин­ным — это задача конкретного анализа. Но человек не может провести этот конкретный анализ для будущих событий и точно сказать, приземлится ли этот самолет или нет, вернется ли на свою базу самолет, идущий на боевое задание, или не вернется. Ни одно из этих суждений не имеет определенного истинностного значения.

Поэтому относительно будущих единичных (конкретных) со­бытий утверждать истинность одного из двух противоречащих суждений можно лишь с определенной степенью вероятности (правдоподобия). Практически люди именно так и поступают, более или менее надеясь на успех и, следовательно, оценивая степень правдоподобия, степень истинности того или иного суж­дения.

Неопределенные ситуации часто обнаруживаются в познании, и не только потому, что такие ситуации имеют место в природе и обществе или процесс познания не завершен, но и потому, что необходимо ввести третье значение истинности — «неопределен­но» — в сами процессы исследования, познания, обучения. Так, например, в социологических анкетах, распространяемых с целью изучения общественного мнения, заранее планируется неопреде­ленность ответа, поэтому, во-первых, должна быть предусмот­рена графа с ответом: «Не знаю», а во-вторых, должен учиты­ваться случай, когда человек вообще не ответит на тот или иной вопрос. При обработке данных социологических обследований на ЭВМ программа для нее должна предусматривать не только случаи определенных ответов: «да» или «нет», но и случаи неоп­ределенных ответов. В процессе программированного обучения с помощью обучающих машин, в частности устройств типа «Экзаменатор», ответы на поставленные вопросы распределяют­ся по трем группам: 1) «истинный ответ (или решение)»; 2) «лож­ный ответ (или решение)»; 3) «не знаю». Итак, в ходе проверки знаний учащихся или студентов с помощью машины заранее с определенной целью вводится третье значение истинности — «неопределенно» — и закон исключенного третьего не действует. В научном и обыденном мышлении людям часто приходится анализировать понятия, обладающие свойством гибкости, подви­жности, не имеющие «жесткого» фиксированного объема (напри­мер, понятие «молодой человек», «старик», «модное платье» и многие другие).

В математике, логике, кибернетике и других науках использу­ются понятия с «жестким», фиксированным объемом, применя­ются алгоритмы, четко предписывающие последовательность операций с этими понятиями. Но в процессе отражения объектив­ной реальности нам приходится в мышлении оперировать и гиб­кими понятиями, встречаться с так называемыми расплывчаты­ми алгоритмами, иметь дело с методами, позволяющими решать задачи, сама постановка которых включает в себя неопределен­ность. В теории «расплывчатых» множеств, оперирующей такими понятиями, закон исключенного третьего и закон непротиворе­чия не применяются.

В приведенных выше примерах охарактеризованы ситуации, в которых закон исключенного третьего или неприменим совсем, или применим ограниченно: в определенной области или на определенном этапе познания. Проанализируем такие ситуации, в которых закон исключенного третьего применим частично.

В процессе голосования разрешается голосовать за принятие резолюции по системе трехзначной логики: «за», «против», «воз­держался», и здесь закон исключенного третьего не действует. Однако подсчет голосов происходит по системе двузначной логи­ки: либо резолюция принята, либо нет, третьего не дано.

К. Маркс писал: «Jus (право. — Ред.) знает только: или — или»¹¹. Действительно, в юридической практике надо доказать суждение, что данный факт (преступление) имел место, или его опровергнуть, и третьего не дано. В случаях кассации вышесто­ящий суд принимает решение опять-таки по закону исключенного третьего: «или виновен — или не виновен, третьего не дано». Но пока не закончено следствие и суждение, скажем, «Сомов виновен в поджоге» еще не доказано и не опровергнуто, оно будет не истинным и не ложным, а неопределенным.

Логические законы следует применять конкретно, в зависимо­сти от свойств тех предметных областей, которые ими отображаются, что полностью относится и к закону непротиворечия, и к закону исключенного третьего.

В познании нередко возникают неопределенные ситуации, ко­торые отражают переходные состояния, имеющиеся как в мате­риальных явлениях, так и в самом процессе познания (например, состояние клинической смерти; ситуации, когда гипотеза еще не подтверждена и не опровергнута; когда мы не знаем, какова степень подтверждения долгосрочного прогноза погоды; рассуж­дения о будущих единичных событиях и т. д.). В такого рода ситуациях мы не можем мыслить только по законам классичес­кой двузначной логики, а прибегаем к трехзначной логике, в ко­торой суждения принимают три значения истинности: истина, ложь и неопределенность. В ряде этих многозначных логик закон непротиворечия не является тождественно-истинной формулой.

Итак, закон исключенного третьего применяется там, где познание имеет дело с жесткой ситуацией: или — или, истина — ложь; там же, где отражается неопределенность в объективных процессах или неопределенность в самом процессе познания, закон исключенного третьего часто не может быть применен. Следовательно, нужен конкретный анализ конкретной ситуации с учетом особенностей предметной области.