Использование определений; понятий в процессе обучения
Определение через род и видовое отличие и номинальное определение широко используются в процессе обучения. Приведем ряд примеров, взятых из школьных учебников. К определениям через ближайший род и видовое отличие можно отнести следующие: «Высшая нервная деятельность — это совокупность множества взаимосвязанных нервных процессов, протекающих в коре головного мозга»; «Наследственностью называют общее свойство всех организмов сохранять и передавать признаки строения и функций от предков к потомству». В учебниках по неорганической химии содержится много номинальных определений понятий, например: «Удержание углем и другими твердыми веществами на своей поверхности частиц газа или растворенного вещества называется адсорбцией». В учебниках физики меньше реальных определений через род и видовое отличие и больше номинальных, например: «Температуру, при которой вещество плавится, называют температурой плавления вещества». В учебнике физики для 7-го класса даны номинальные определения следующим понятиям: «теплопередача», «температура отвердевания (или кристаллизации)», «удельная теплота плавления», «испарение», «конденсация», «температура кипения», «удельная теплота парообразования», «сила тока», «электрическая сила» и многим другим. Имеются там и реальные определения. В учебниках географии, наоборот, преимущественное место занимают реальные определения через род и видовое отличие. Например, «Минерал — природное образование (тело), однородное по химическому составу и физическим свойствам». Много определений в учебниках математики, русского языка, истории, литературы и других. Определение понятий — один из важных и распространенных способов передачи информации в концентрированном виде.
Учитель, овладевая методикой преподавания своего предмета, должен в первую очередь организовать работу с основными, опорными понятиями и законами, уметь выделить главное в обучении. Повышению теоретического уровня преподавания способствует четкое выделение основных понятий. Надо не только отрабатывать признаки основных и опорных понятий, но и органично увязывать их содержание с современностью, с практикой, в противном случае может возникнуть формализм в знаниях учащихся.
Четкое определение понятия «культура» поможет устранить недостаток в знаниях учащихся, состоящий в том, что они редко относят развитие орудий труда, техники к достижениям культуры, ограничивая свои представления памятниками зодчества, скульптуры, книгопечатания, прикладного искусства, т. е. недостаточно глубоко изучают достижения материальной культуры. Соответственно двум основным видам производства — материального и духовного — культуру принято делить на материальную и духовную, поэтому учителя должны более четко раскрывать содержание понятии «материальная культура» и «духовная культура» и на их базе формировать более общее понятие «культура».
В целом перед учителями стоят такие задачи: добиваться от учащихся глубокого усвоения основных понятий курса, выработки цельной системы раскрытия важнейших понятий школьных предметов, поэтапного расширения их объема и усложнения их структуры. Таков путь усвоения основных, опорных понятий, изучаемых в школьных курсах.
Правила явного определения. Ошибки, возможные в определении
1. Определение должно быть соразмерным, т. е. объем определяющего понятия должен быть равен объему определяемого понятия. 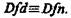 Это правило часто нарушается, в результате,
Это правило часто нарушается, в результате,
чего возникают логические ошибки в определении. Типы этих логических ошибок:
а) широкое определение, когда Dfd<Dfn. Такая ошибка содержится в следующих определениях: «Гравитация — это взаимодействие двух материальных тел». «Лошадь — млекопитающее и позвоночное животное». (Здесь понятие «лошадь» нельзя отличить от понятий «корова» или «коза».) Понятие «окружность» неправильно определяется так: «Это фигура, которая описывается движущимся концом отрезка, когда другой его конец закреплен, или фигура, которая образована движущимся концом циркуля». С помощью этого определения нельзя отличить понятие «окружность» от понятия «дуга», так как не указано, что окружность — это кривая замкнутая линия;
б) узкое определение, когда Dfd>Dfh. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?). «Производительными силами называются орудия труда, а также и сами люди с их умениями и приемами труда». (В производительные силы входят все средства производства, а не только орудия труда.);
в) определение в одном отношениии широкое, в другом — узкое. В этих неправильных определениях Dfd>Dfn и Dfd<Dfn (в разных отношениях). Например, «Бочка — сосуд для хранения жидкостей». С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайник, и ведро, и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей. Аналогичная ошибка содержится в определении понятия «учитель»: «Учитель — человек, обучающий детей».
2. Определение не должно содержать круга. Круг возникает тогда, когда Dfd определяется через Dfn, a Dfn был определен через Dfd. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («ось — это прямая, вокруг которой происходит вращение»).
Круг возникает и тогда, когда определяемое понятие характеризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавтологий.
В. И. Ленин, выявив эту логическую ошибку у П. Струве, который дал неверное определение понятия «хозяйство», писал: «Хозяйство определяется через хозяйствование! Масляное масло...»5
Тавтологичны такие определения: «Халатность заключается в том, что человек халатно относится к своим обязанностям»; «Количество — это характеристика предмета с его количественной стороны».
Логически некорректным является употребление в мышлении (и в речи) тавтологий, таких, например, как масляное масло, трудоемкий труд, порученное поручение, прогрессирующий прогресс, ладанная задача, изобрету изобретение, поиграем в игру, памятный сувенир, подытожим итоги и др. Иногда можно встретить выражения вида: «Закон есть закон», «Жизнь есть жизнь» и т. д., которые представляют собой прием усиления, а не сообщения в предикате какой-то информации о субъекте, так как субъект и предикат тождественны. Такие выражения не претендуют на определение соответствующего понятия: «закон», «жизнь» или др.
3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их - метафорами, сравнениями и т. д.
Не будут определениями следующие суждения: «Архитектура — застывшая музыка», «Лев — царь зверей», «Верблюд — корабль пустыни», «Такт — это разум сердца» (К. Гуцков), «Неблагодарность — род слабости» (И. В. Гёте).
Неявные определения
Вотличие от явных определений, имеющих структуру  в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.
в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.
Контекстуальное определение позволяет выяснить содержание незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода, если текст дан на иностранном языке, или к толковому словарю, если текст дан на родном языке.
Значения неизвестных в уравнениях даны в неявном виде. Если дано уравнение, первой степени, например 10—y=3, или дано квадратное уравнение, например х2 — 7x+12=0, то, решая их и находя значение корней этих уравнений, мы даем явное определение для у (у =7) и для х (x1 = 4 и х2 = 3).
Индуктивные определения характеризуются тем, что определяемый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивного определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»:
1.1 — натуральное число.
2. Если n — натуральное число, то n +1 — натуральное число.
3. Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет.
С помощью этого индуктивного определения получается натуральный ряд чисел: 1, 2, 3, 4.....Таков алгоритм построения натуральных чисел.
Определение через аксиомы
В современной математике и в математической логике широко применяется так называемый аксиоматический метод. Приведем пример6. Пусть дана система каких-то элементов (обозначаемых х, у, z.,.), и между ними установлено отношение, выражаемое термином «предшествует». Не определяя ни самих объектов, ни отношения «предшествует», мы высказываем для них следующие утверждения (т. е. следующие две аксиомы):
1. Никакой объект не предшествует сам себе.
2. Если х предшествует у, а у предшествует z, то х предшествует z.
Так с помощью двух аксиом определены системы объектов вида « x предшествует у». Например, пусть объектами х, у... являются люди, а отношение между х и у представляет собой «х старше у». Тогда выполняются утверждения 1 и 2. Если объекты х, у, z — действительные числа, а отношение <x предшествует у» представляет собой < x меньше у», то утверждения 1 и 2 также выполняются. Утверждения (т. е. аксиомы) 1 и 2 определяют системы объектов с одним отношением.
