Задания для самостоятельной работы. Лабораторная работа № 125
Лабораторная работа № 125.
Равносильность формул.
Цель работы.Изучить логические операции и основные равносильности алгебры логики, научиться преобразовывать формулы, используя основные равносильности и правила поглощения.
Логические операции
 - отрицание, Ú - дизъюнкция, Ù (&) - конъюнкция,
- отрицание, Ú - дизъюнкция, Ù (&) - конъюнкция,
« (~) - эквиваленция, ® - импликация
Приоритет операций:
конъюнкция, дизъюнкция, эквиваленция и импликация
Таблица истинности
| A | B |  | A Ú B | A & B | A « B | A ® B |
Основные равносильности алгебры логики:
 1.
1.  º A 2. A & B º B & A
º A 2. A & B º B & A
3. A Ú B º B Ú A 4. (A & B) & C º A & (B & C)
5. (A Ú B) Ú C º A Ú (B Ú C) 6. A & (B Ú C) º (A & B) Ú (A & C)
7. A Ú (B & C) º (A Ú B) & (A Ú C) 8. A & A º A
9. A Ú A º A 10. (A & B) Ú A º A
 11. (A Ú B) & A º A 12. A & B º
11. (A Ú B) & A º A 12. A & B º  Ú
Ú 
 13. A Ú B º
13. A Ú B º  &
&  14. A & 1 º A
14. A & 1 º A
15. A & 0 º 0 16. A Ú 1 º 1
17. A Ú 0 º A 18. A Ú  º 1
º 1
19. A &  º 0 20. A ® B º
º 0 20. A ® B º  Ú B
Ú B
21. A « B º (A ® B) & (B ® A) º AB Ú 

22. A Ú  B º A Ú B
B º A Ú B
Студенты с четными номерами по списку группы выполняют 2, 4, 6, 8, 10 задания, с нечетными номерами выполняют задания 1, 3, 5, 7, 9.
Задание 1.Используя основные равносильности алгебры логики, упростить формулы:
1) 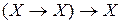 ; 2)
; 2) 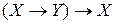 ; 3)
; 3) 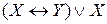 ; 4)
; 4) 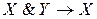 ;
;
5) 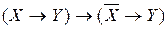 ; 6)
; 6) 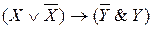 ; 7)
; 7) 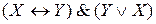 ;
;
8) 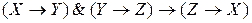 ;
;
9) 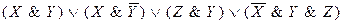 .
.
Методические указания.
Пример 1. Используя основные равносильности алгебры логики, а также равносильности 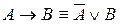 и
и 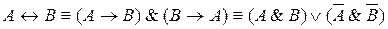 ,
,
упростить формулу: 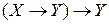 .
.
Решение.
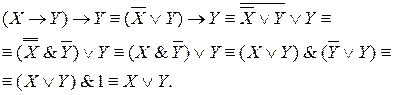
Ответ: 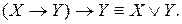
Логическую операцию конъюнкция в формулах алгебры логики можно опускать, т.е. выражение A&B можно записывать в виде АВ.
Пример 2. Для заданного высказывания 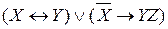
1) построить таблицу истинности;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
Решение.
1) Таблица истинности. Пусть 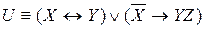
| Х | Y | Z | 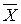 | YZ | 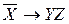 | 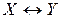 | U |
2) Выполним равносильные преобразования, используя 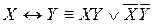 и
и 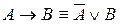 , имеем:
, имеем:
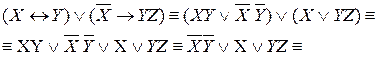
в последнем преобразовании для первого и третьего слагаемых использовали правило поглощения АВÚАºА, далее используем другое правило поглощения 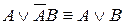 , получаем
, получаем
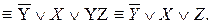
Еще раз использовали правило поглощения.
3) Для полученного выражения 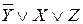 построим таблицу истинности
построим таблицу истинности
| Х | Y | Z | 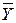 | 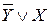 | 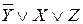 |
Результирующие (последние) столбцы в двух таблицах совпали, следовательно, выполненные преобразования верны.
Задания для самостоятельной работы
Для заданного логического выражения (высказывания):
1) построить таблицу истинность;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
| Вариант | Вариант | ||
(A « C) Ú A  Ú B Ú B | (A ® B) Ú A 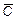 Ú BC Ú BC | ||
(AB ® C) Ú A 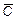 |  C Ú (AB « C) C Ú (AB « C) | ||
(  ® C) (B ® C) (B 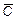 Ú AC) Ú AC) | (A ~ B) Ú  C Ú AB C Ú AB | ||
(A ® B) Ú A  Ú AC Ú AC | (A ~ B) Ú A 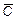 Ú AC Ú AC | ||
(AC ® B) Ú B 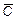 | (AC ® B) Ú A 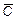 | ||
(  ® B) ( ® B) ( 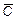 Ú AC) Ú AC) | (  « C) (A « C) (A 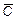 ® BC) ® BC) | ||
(A ® C) Ú A  Ú Ú  B B | (C ® A  ) Ú ) Ú  Ú BC Ú BC | ||
(BC ®  ) ÚAB ) ÚAB 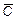 | C Ú (AB « C) Ú B 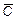 | ||
(AB ® C) Ú AB 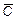 | (  ~ B) (A ~ B) (A 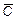 ® CB) ® CB) | ||
| (B ® AC) Ú (AB ® C) | (  B ® C) Ú B Ú B ® C) Ú B Ú  C C | ||
(A « B) Ú (A  ® BC) ® BC) | (  C ® C ® 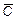 ) Ú ) Ú  BC BC | ||
(AB ®  C) Ú A C) Ú A 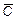 | (  B ® C) (A ~ C) B ® C) (A ~ C) | ||
(  « BC) (A « BC) (A  ® BC) ® BC) | (A ®  B) ( B) (  B ® B ®  C) C) | ||
(A  « C) Ú A « C) Ú A  C Ú B C Ú B | (A ® B) Ú A 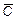 Ú BC Ú BC | ||
(  ® AC) Ú A ® AC) Ú A  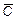 |  C Ú (AB « C) C Ú (AB « C) | ||
(  ® BC) ( ® BC) (  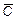 Ú AB) Ú AB) | (A ~ B) Ú  C Ú AB C Ú AB | ||
(A  ® BC) Ú ® BC) Ú  C Ú AB C Ú AB | (A ~ B) Ú A 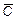 Ú AC Ú AC |
Контрольные вопросы.
1. Какие основные логические операции вам известны?
2. Перечислите основные равносильности алгебры логики.
